浙江省温州市“温州新希望联盟”2021届九年级上学期数学第一次月考试卷
试卷更新日期:2020-10-28 类型:月考试卷
一、选择题
-
1. 下列各式中, 是关于 的二次函数的是( ).A、 B、 C、 D、2. 下列说法正确的是( ).A、“明天降雨的概率是60%”表示明天有60%的时间都在降雨 B、“抛一枚硬币反面朝上的概率为 ”表示每抛2次就有1次反面朝上 C、“抛一枚均匀的正方体骰子, 朝上的点数是5的概率为 ”表示随着抛掷次数的增加,“抛出朝上的点数是5”这一事件发生的频率稳定在 左右 D、“彩票中奖的概率为1%”表示买100张彩票肯定会中奖3. 如图,是国旗中的一颗五角星图案,绕着它的中心旋转,要使旋转后的五角星能与自身重合,则旋转角的度数至少为( ).
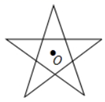 A、30° B、45° C、60° D、72°4. 在△ 中,已知 , , 是 的中点,以 为圆心作一个 为半径的圆 ,则 , , 三点在圆 内的有( )个.
A、30° B、45° C、60° D、72°4. 在△ 中,已知 , , 是 的中点,以 为圆心作一个 为半径的圆 ,则 , , 三点在圆 内的有( )个.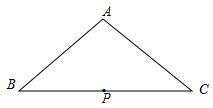 A、0 B、1 C、2 D、35. 已知 , 是函数 上的点,则( ).A、 B、 C、 D、 , 的大小关系不确定6. 已知二次函数 的图象如图所示,那么关于 的一元二次方程 的两个解为( ).
A、0 B、1 C、2 D、35. 已知 , 是函数 上的点,则( ).A、 B、 C、 D、 , 的大小关系不确定6. 已知二次函数 的图象如图所示,那么关于 的一元二次方程 的两个解为( ). A、-1,3 B、-2,3 C、1,3 D、3,47. 布袋中有红、黄、蓝三种颜色的球各一个,从中摸出一个球之后不放回布袋,再摸第二个球,这时得到的两个球的颜色中有“一红一黄”的概率是( )
A、-1,3 B、-2,3 C、1,3 D、3,47. 布袋中有红、黄、蓝三种颜色的球各一个,从中摸出一个球之后不放回布袋,再摸第二个球,这时得到的两个球的颜色中有“一红一黄”的概率是( )
A、 B、 C、 D、8. 函数 与抛物线 的图象可能是( ).A、 B、
B、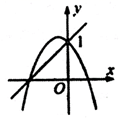 C、
C、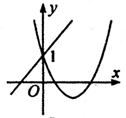 D、
D、 9. 已知二次函数 的y与x的部分对应值如下表:
9. 已知二次函数 的y与x的部分对应值如下表:x
-1
0
1
3
y
-3
1
3
1
下列结论:①抛物线的开口向下;②其图象的对称轴为直线 ;③当 时,函数值y随x的增大而增大;④方程 有一个根大于4,其中正确的结论有( )
A、1个 B、2个 C、3个 D、4个10. 抛物线 (其中 , 是常数)过点 ,且抛物线的对称轴与线段 有交点,点 的坐标为 ,点 的坐标为 ,则 的值不可能是( ).A、9 B、11 C、13 D、15二、填空题
-
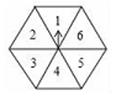
11. 抛物线 与 轴的交点坐标是.12. 如图,任意转动正六边形转盘一次,当转盘停止转动时,指针指向大于3的数的概率是 .
 13. 已知 的面积为 .若点 在 内,那么线段 的长度 的取值范围是.14. 在平面直角坐标系,将抛物线 由左平移3个单位,再向上平移2个单位,得到的抛物线解析式为.15. 如图,在平面直角坐标系中,抛物线 经过坐标原点 ,与 轴的另一个交点为 ,且 ,过抛物线的顶点 分别作 轴于 、 轴于 ,则图中阴影部分图形的面积的和为.
13. 已知 的面积为 .若点 在 内,那么线段 的长度 的取值范围是.14. 在平面直角坐标系,将抛物线 由左平移3个单位,再向上平移2个单位,得到的抛物线解析式为.15. 如图,在平面直角坐标系中,抛物线 经过坐标原点 ,与 轴的另一个交点为 ,且 ,过抛物线的顶点 分别作 轴于 、 轴于 ,则图中阴影部分图形的面积的和为. 16. 抛物线 与 轴交于两点,分别是 , ,则 .17. 如图,抛物线 与 轴交于 , 两点, 是以点 为圆心,1为半径的圆上的动点, 是线段 的中点,连接 , ,则线段 的最小值是.
16. 抛物线 与 轴交于两点,分别是 , ,则 .17. 如图,抛物线 与 轴交于 , 两点, 是以点 为圆心,1为半径的圆上的动点, 是线段 的中点,连接 , ,则线段 的最小值是. 18. 当 时,关于 的一元二次方程 只有一个实数解,则 的取值范围为.
18. 当 时,关于 的一元二次方程 只有一个实数解,则 的取值范围为.三、解答题
-
19. 如图1,图2,在 的方格上建立平面直角坐标系(小方格的单位长度为1), , , , , , 都在格点上.
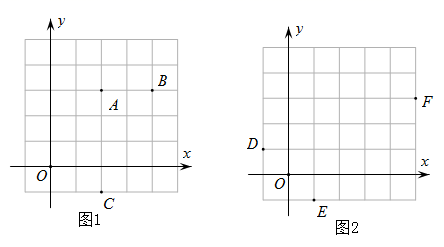 (1)、请在图1中作出经过 , , 三点的圆,并求出圆的半径.(2)、请在图2中作出经过 , , 三点的圆,并求出圆的半径.20. 已知抛物线 的图象经过点 ,且当 时,函数有最大值为4.(1)、求函数表达式;(2)、直接写出:当 取何值时,函数值大于1.21. 在3件同型号的产品 、 、 中, 为不合格产品,其余2件为合格产品.(1)、从这3件产品中随机抽取2件进行检测,请用树状图或列表法求出抽到的2件都是合格品的概率;(2)、在这3件产品中加入 件合格品后,进行如下试验:随机抽取1件进行检测,然后放回,多次重复这个试验,通过大量重复试验后发现,抽到合格品的概率稳定在 ,则可以推算出 的值大约是多少?22. 如图,线段 过圆心 交 于 , 两点, 交 于点 ,且 .
(1)、请在图1中作出经过 , , 三点的圆,并求出圆的半径.(2)、请在图2中作出经过 , , 三点的圆,并求出圆的半径.20. 已知抛物线 的图象经过点 ,且当 时,函数有最大值为4.(1)、求函数表达式;(2)、直接写出:当 取何值时,函数值大于1.21. 在3件同型号的产品 、 、 中, 为不合格产品,其余2件为合格产品.(1)、从这3件产品中随机抽取2件进行检测,请用树状图或列表法求出抽到的2件都是合格品的概率;(2)、在这3件产品中加入 件合格品后,进行如下试验:随机抽取1件进行检测,然后放回,多次重复这个试验,通过大量重复试验后发现,抽到合格品的概率稳定在 ,则可以推算出 的值大约是多少?22. 如图,线段 过圆心 交 于 , 两点, 交 于点 ,且 . (1)、若 ,求 的度数;(2)、若 , ,求 的长.23. 知识链接:弹道导弹飞行轨迹可以分为三个阶段.第一阶段:导弹点火后,垂直向上飞行阶段;第二阶段:导弹进入安全预定高度,以曲线路线飞行阶段(最高点称为轨道的远地点);第三阶段:发动机熄火后,导弹弹头与弹体分离,以惯性飞向目标阶段.
(1)、若 ,求 的度数;(2)、若 , ,求 的长.23. 知识链接:弹道导弹飞行轨迹可以分为三个阶段.第一阶段:导弹点火后,垂直向上飞行阶段;第二阶段:导弹进入安全预定高度,以曲线路线飞行阶段(最高点称为轨道的远地点);第三阶段:发动机熄火后,导弹弹头与弹体分离,以惯性飞向目标阶段.某洲际导弹发射后,计算机隔一段时间(单位:分)对导弹离地高度(单位:千米)进行数据采集,对这些数据进行列表统计后得到如下表格:
时间
0
1
2
4
5
6
9
13
14
16
19
24
…
离地高度
0
24
96
386
514
616
850
994
1000
976
850
400
…
已知导弹在第 分钟( 为整数)开始进入飞行第二阶段,在下落过程中距离地面100千米时进入第三阶段.
(1)、该导弹在发射多少时间后达到轨道的远地点,此时距离地面的高度是多少千米?(2)、请用学过的函数模型来确定第二阶段的曲线解析式,并求出 的值.(3)、求导弹发射多少时间后发动机熄火?(结果保留根号)24. 如图,已知抛物线 交 轴于 , 两点,交 轴于点 ,点 是线段 上一动点. (1)、求抛物线解析式;(2)、连接 并延长交抛物线于点 ,连接 ,是否存在点 使 ?若存在,请求出点 的坐标;若不存在,请说明理由;(3)、连接 ,过点 作 交 轴于点 ,点 绕点 逆时针旋转,当点 的对应点 恰好落在 轴上时, ,求此时 的坐标.
(1)、求抛物线解析式;(2)、连接 并延长交抛物线于点 ,连接 ,是否存在点 使 ?若存在,请求出点 的坐标;若不存在,请说明理由;(3)、连接 ,过点 作 交 轴于点 ,点 绕点 逆时针旋转,当点 的对应点 恰好落在 轴上时, ,求此时 的坐标.