浙江省绍兴市2021届九年级上学期数学10月月考试卷
试卷更新日期:2020-10-28 类型:月考试卷
一、选择题(本大题有10题,每小题4分,共40分)
-
1. 在一个不透明的袋子里装有红球、黄球共20个,这些球除颜色外都相同.小敏通过多次实验发现,摸出红球的频率稳定在 0.25 左右,则袋子中红球的个数最有可能是( )A、5 B、10 C、12 D、152. 掷一枚质地均匀的硬币5次,其中3次正面朝上,2次正面朝下,则再次掷出这枚硬币,正面朝下的概率是( )A、1 B、 C、 D、3. 下列说法中,正确的是( )A、“掷一次质地均匀的骰子,向上一面的点数是6”是必然事件 B、“经过有交通信号灯的路口,遇到红灯”是随机事件 C、“发热病人的核酸检测呈阳性”是必然事件 D、“13个同学参加一个聚会,他们中至少有两个同学的生日在同一个月”是不可能事件4. 要将抛物线y=x2+2x+3平移后得到抛物线y=x2 , 下列平移方法正确的是( )A、向左平移1个单位,再向上平移2个单位 B、向左平移1个单位,再向下平移2个单位 C、向右平移1个单位,再向上平移2个单位 D、向右平移1个单位,再向下平移2个单位5. 新冠疫情发生以来,为保证防控期间的口罩供应,某公司加紧转产,开设多条生产线争分夺秒赶制口罩,从最初转产时的陌生,到正式投产后达成日均生产100万个口罩的产能.不仅效率高,而且口罩送检合格率也不断提升,真正体现了“大国速度”.以下是质监局对一批口罩进行质量抽检的相关数据,统计如下:
抽检数量n/个
20
50
100
200
500
1000
2000
5000
10000
合格数量m/个
19
46
93
185
459
922
1840
4595
9213
口罩合格率
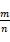
0、950
0、920
0、930
0、925
0、918
0、922
0、920
0、919
0、921
下面四个推断合理的是( )
A、当抽检口罩的数量是10000个时,口罩合格的数量是9213个,所以这批口罩中“口罩合格”的概率是0.921. B、由于抽检口罩的数量分别是50和2000个时,口罩合格率均是0.920,所以可以估计这批口罩 中“口罩合格”的概率是0.920. C、随着抽检数量的增加,“口罩合格”的频率总在0.920附近摆动,显示出一定的稳定性,所以可以估计这批口罩中“口罩合格”的概率是0.920. D、当抽检口罩的数量达到20000个时,“口罩合格”的概率一定是0.921.6. 给出下列函数:①y=﹣3x+2;②y= ;③y=2x2;④y=3x,上述函数中符合条作“当x>1时,函数值y随自变量x增大而增大“的是( )A、①③ B、③④ C、②④ D、②③7. 如图,小敏随意向水平放置的大正方形内部区域抛一个小球,则小球停在小正方形内部(阴影)区域的概率为( )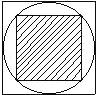 A、 B、 C、 D、8. 方程x2+2x+1=的正数根的个数为( )A、0 B、1 C、2 D、39. “闻起来臭,吃起来香”的臭豆腐是绍兴特色小吃,臭豆腐虽小,但制作流程却比较复杂,其中在进行加工煎炸臭豆腐时,我们把焦脆而不糊的豆腐块数的百分比称为“可食用率”,在特定条件下,“可食用率”p与加工煎炸的时间t(单位:分钟)近似满足函数关系式: ( a,b,c为常数),如图纪录了三次实验数据,根据上述函数关系和实验数据,可以得到加工煎炸臭豆腐的最佳时间为( )
A、 B、 C、 D、8. 方程x2+2x+1=的正数根的个数为( )A、0 B、1 C、2 D、39. “闻起来臭,吃起来香”的臭豆腐是绍兴特色小吃,臭豆腐虽小,但制作流程却比较复杂,其中在进行加工煎炸臭豆腐时,我们把焦脆而不糊的豆腐块数的百分比称为“可食用率”,在特定条件下,“可食用率”p与加工煎炸的时间t(单位:分钟)近似满足函数关系式: ( a,b,c为常数),如图纪录了三次实验数据,根据上述函数关系和实验数据,可以得到加工煎炸臭豆腐的最佳时间为( ) A、3.50分钟 B、4.05分钟 C、3.75分钟 D、4.25分钟10. 如图,在四边形 ABCD 中, AD∥BC , ∠A=45° , ∠C=90° , AD=4cm ,CD=3cm 、动点M,N同时从点A出发,点M以 cm/s 的速度沿 AB 向终点B运动,点N以2cm/s 的速度沿折线 AD-DC 向终点C运动.设点N的运动时间为ts ,△AMN 的面积为 Scm² ,则下列图象能大致反映S与t之间函数关系的是( )
A、3.50分钟 B、4.05分钟 C、3.75分钟 D、4.25分钟10. 如图,在四边形 ABCD 中, AD∥BC , ∠A=45° , ∠C=90° , AD=4cm ,CD=3cm 、动点M,N同时从点A出发,点M以 cm/s 的速度沿 AB 向终点B运动,点N以2cm/s 的速度沿折线 AD-DC 向终点C运动.设点N的运动时间为ts ,△AMN 的面积为 Scm² ,则下列图象能大致反映S与t之间函数关系的是( )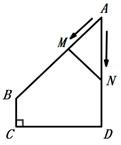 A、
A、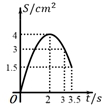 B、
B、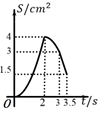 C、
C、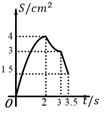 D、
D、
二、填空题(本大题有6题,每小题5分,共30分)
-
11. 已知二次函数 ,当x>0时,y随x的增大而(填“增大”或“减小”)12. 将二次函数y=x2﹣2x+3化为y=(x﹣h)2+k的形式,则h= , k=.13. 经过十字路口红绿灯处的两辆汽车,可能直行,也可能向右转,如果这两种可能性大小相同,则至少有一辆向右转的概率是.14. 将抛物线 向上平移3个单位长度后,经过点(-2,5),则 的值是.15. 汽车刹车后行驶的距离s与行驶时间t(秒)的函数关系是s=12t﹣4t2 ,汽车从刹车后到停下来前进了米.16. 已知关于 x 的二次函数 的图象开口向下, y 与 x 的部分对应值如下表所示:
x
-3
-2
-1
0
1
y
0
m
t
n
0
下列判断,① ;② ;③方程 有两个不相等的实数根;
④若 ,则 ,正确的是(填写正确答案的序号) .
三、解答题(本大题有8题,第17-20小题每小题8分,第21小题10分,第22,23小题每小题12分,第24小题14分,共80分)
-
17. 已知抛物线的顶点坐标是(2,-3),且经过点(1,-2.5)(1)、求这个抛物线的函数表达式,并作出这个函数的大致图像.(2)、当x在什么范围内时,y随x的增大而减小?18. 在一个不透明的袋子中装有三个小球,分别标有数字﹣2、2、3,这些小球除数字不同外其余均相同,现从袋子中随机摸出一个小球记下数字后放回,搅匀后再随机摸出一个小球,用画树状图或列表的方法,求两次摸出的小球上数字之和是正数的概率.19. 已知抛物线y=x2+(n﹣3)x+n+1经过坐标原点O,与x轴交于另一点A,顶点为B.求:(1)、抛物线的解析式与△AOB的面积;(2)、要使二次函数的图象过点(10,0),应把图象沿x轴向右平移个单位.20. 小敏、小聪两同学做游戏,游戏规则是:一个不透明的文具袋中,装有型号完全相同的3支红笔和2支黑笔,两人先后从袋中取出一支笔(不放回),若两人所取笔的颜色相同,则小敏胜,否则,小聪胜.(1)、请用树形图或列表法列出摸笔游戏所有可能的结果;(2)、请计算小敏获胜的概率,并指出本游戏规则是否公平?若不公平,你认为对谁有利.21. 如图,在某场足球比赛中,球员甲从球门底部中心点O的正前方10m处起脚射门,足球沿抛物线飞向球门中心线;当足球飞离地面高度为3m时达到最高点,此时足球飞行的水平距离为6m.已知球 门的横梁高OA为2.44m.
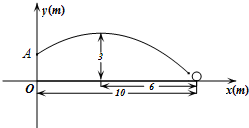 (1)、在如图所示的平面直角坐标系中,问此飞行足球能否进球门?(不计其它情况)(2)、守门员乙站在距离球门2m处,他跳起时手的最大摸高为2.52m,他能阻止球员甲的此次射门吗?如果不能,他至少后退多远才能阻止球员甲的射门?22. 经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转,如果这三种情况是等可能的, 当三辆汽车经过这个十字路口时:(1)、求三辆车全部同向而行的概率;(2)、求至少有两辆车向左转的概率;(3)、由于十字路口右拐弯处是通往新建经济开发区的,因此交管部门在汽车行驶高峰时段对车流量作了统计,发现汽车在此十字路口向右转的频率为 ,向左转和直行的频率均为 .目前在此路口,汽车左转、右转、直行的绿灯亮的时间分别为30秒,在绿灯亮总时间不变的条件下,为了缓解交通拥挤,请你用统计的知识对此路口三个方向的绿灯亮的时间做出合理的调整.23. 某商场要经营一种新上市的文具,进价为20元,试营销阶段发现:当销售单价是25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件.(1)、写出商场销售这种文具,每天所得的销售利润W(元)与销售单价x(元)之间的函数关系式;(2)、求销售单价为多少元时,该文具每天的销售利润最大;(3)、商场的营销部结合上述情况,提出了A、B两种营销方案.
(1)、在如图所示的平面直角坐标系中,问此飞行足球能否进球门?(不计其它情况)(2)、守门员乙站在距离球门2m处,他跳起时手的最大摸高为2.52m,他能阻止球员甲的此次射门吗?如果不能,他至少后退多远才能阻止球员甲的射门?22. 经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转,如果这三种情况是等可能的, 当三辆汽车经过这个十字路口时:(1)、求三辆车全部同向而行的概率;(2)、求至少有两辆车向左转的概率;(3)、由于十字路口右拐弯处是通往新建经济开发区的,因此交管部门在汽车行驶高峰时段对车流量作了统计,发现汽车在此十字路口向右转的频率为 ,向左转和直行的频率均为 .目前在此路口,汽车左转、右转、直行的绿灯亮的时间分别为30秒,在绿灯亮总时间不变的条件下,为了缓解交通拥挤,请你用统计的知识对此路口三个方向的绿灯亮的时间做出合理的调整.23. 某商场要经营一种新上市的文具,进价为20元,试营销阶段发现:当销售单价是25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件.(1)、写出商场销售这种文具,每天所得的销售利润W(元)与销售单价x(元)之间的函数关系式;(2)、求销售单价为多少元时,该文具每天的销售利润最大;(3)、商场的营销部结合上述情况,提出了A、B两种营销方案.方案A:该文具的销售单价高于进价且不超过30元;
方案B:每天销售量不少于10件,且每件文具的利润至少为25元.
请比较哪种方案的最大利润更高,并说明理由?
24. 如图,抛物线y=ax2+bx+c(a≠0)的图象经过A(1,0),B(3,0),C(0,6)三点. (1)、求抛物线的解析式.(2)、抛物线的顶点M与对称轴l上的点N关于x轴对称,直线AN交抛物线于点D , 直线BE交AD于点E , 若直线BE将△ABD的面积分为1:2两部分,求点E的坐标.(3)、P为抛物线上的一动点,Q为对称轴上动点,抛物线上是否存在一点P , 使A、D、P、Q为顶点的四边形为平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式.(2)、抛物线的顶点M与对称轴l上的点N关于x轴对称,直线AN交抛物线于点D , 直线BE交AD于点E , 若直线BE将△ABD的面积分为1:2两部分,求点E的坐标.(3)、P为抛物线上的一动点,Q为对称轴上动点,抛物线上是否存在一点P , 使A、D、P、Q为顶点的四边形为平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.