浙江省绍兴市柯桥区2020-2021学年八年级上学期数学10月月考试卷
试卷更新日期：2020-10-28 类型：月考试卷
一、 单选题（共10题；共20分）
-
1. 三角形的两边分别为6，10，则第三边的长可能等于（ ）A、3 B、11 C、16 D、172. 下列图形中，是轴对称图形的是（ ）A、
B、
C、
D、
3. 等腰三角形的两边长为3和8，则这个等腰三角形的周长是（ ）A、14 B、19 C、14或19 D、204. 如图，∠1=∠2，AB=EB，CB=DB，则△ABD≌△EBC时，运用的判定定理是（）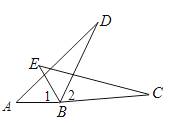
A、SSS B、ASA C、AAS D、SAS5. 下列命题的逆命题是真命题的是（ ）A、如果两个角是直角，那么它们相等 B、全等三角形的对应角相等 C、两直线平行，内错角相等 D、对顶角相等6. 根据下列条件不能判断△ABC是直角三角形的是（ ）A、∠B=50°，∠C=40° B、∠B=∠C=45° C、∠A=2∠B=3∠C D、∠A：∠B：∠C=5:3:27. 等腰三角形一腰上的高与底边所夹的角（ ）A、等于顶角 B、等于顶角的一半 C、等于顶角的2倍 D、等于底角的一半8. 如图，依据尺规作图的痕迹，计算∠α=（ ）
A、68° B、56° C、28° D、34°9. 如图，方格纸中△DEF的三个顶点分别在小正方形的顶点上，像这样的三个顶点都在格点上的三角形叫格点三角形，则图中与△DEF全等的格点三角形最多有（ ）个．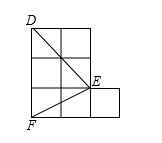
A、8 B、7 C、6 D、410. 如图，已知AB＝AC，AF＝AE，∠EAF＝∠BAC，点C、D、E、F共线．则下列结论，其中正确的是（ ）
①△AFB≌△AEC；②BF＝CE；③∠BFC＝∠EAF；④AB＝BC．
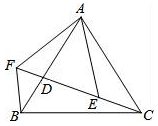A、①②③ B、①②④ C、①② D、①②③④二、填空题（共10题；共30分）
-
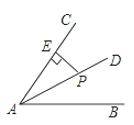
11. 等边三角形有条对称轴。12. 将命题“有一个内角是直角的三角形是直角三角形”改写成如果……那么……的形式．13. 如图，点P是∠BAC的平分线AD上一点，PE⊥AC于点E．已知PE=5，则点P到AB的距离是 ．
14. 如图，已知EB=FD，∠EBA=∠FDC，∠E=∠F，AD=10，BC=4，则AC=。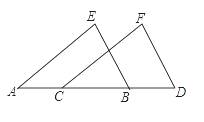
15. 如图，O是△ABC内一点，∠OBC= ∠ABC，∠OCB= ∠ACB，若∠A=66°，则∠BOC=度．
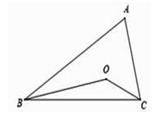16. 如图，D、E分别是△ABC边AB、BC上的点，AD=2BD，BE=CE，若S△ABC=6，设△ADF的面积为S1 ， △CEF的面积为S2 ， 则S1-S2的值是。
17. 我们规定：等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“特征值”，记作k，若k= ，则该等腰三角形的顶角为度．18. 如图，等腰三角形ABC的底边BC长为4，面积是18，腰AC的垂直平分线EF分别交AC，AB边于E，F点．若点D为BC边的中点，点G为线段EF上一动点，则△CDG周长的最小值为。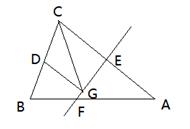
19. 如图，已知点P是射线BM上一动点（P不与B重合），∠AOB=30°，∠ABM=60°，当∠OAP=时，以A、O、B中的其中两点和P点为顶点的三角形是等腰三角形．
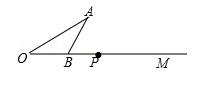20. 如图，在△ABC中，点D为BC的中点，△AEF的边EF过点C，且AE=EF，AB∥EF，AD平分∠BAE，CE=2，AB=9，则CF= ．
三、解答题（共50分）
-
21. 如图，已知点B ， E在线段CF上，CE＝BF ， AC//DF，∠C＝∠F ， ∠ABC＝∠DEF ．
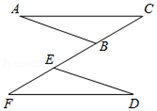
求证：AC=DF．
解：∵CE＝BF（已知）
∴CE﹣BE＝BF﹣BE（）
即BC＝EF
∵AC//DF
∴∠C＝（）
在△ABC和△DEF中
，
∴△ABC≌△DEF（）．
∴AC=DF.（）
22. 如图，在正方形网格上的一个△ABC ， 且每个小正方形的边长为1（其中点A ， B ， C均在网格上）．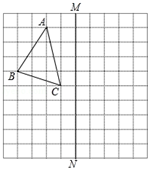
（ 1 ）作△ABC关于直线MN的轴对称图形△A′B′C′；
（ 2 ）在MN上画出点P ， 使得PA+PC最小；
23. 已知，如图，AC、BD相交于点E ， AB＝DC ， AC＝DB ． 求证：∠A=∠D．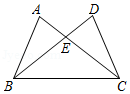
24. 如图，在△ABD和△ACE中，有下列四个等式：①AB=AC；②AD=AE；③∠1=∠2；④BD=CE．以其中三个条件为题设，填入已知栏中，一个论断为结论，填入下面求证栏中，使之组成一个真命题，并写出证明过程．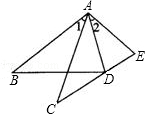
已知：．
求证：．
证明：
25. 如图，已知△ABC中，∠ABC＝∠ACB ， 以点B为圆心，BC长为半径的弧分别交AC ， AB于点D ， E ， 连接BD ， ED ．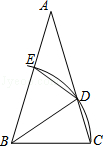
(1)、写出图中所有的等腰三角形；(2)、若∠AED＝114°，求∠ABD和∠ACB的度数．26.
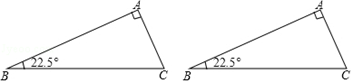(1)、操作实践：△ABC中，∠A=90°，∠B=22.5°，请画出一条直线把△ABC分割成两个等腰三角形，并标出分割成两个等腰三角形底角的度数；（要求用两种不同的分割方法）(2)、分类探究：△ABC中，最小内角∠B=24°，若△ABC被一直线分割成两个等腰三角形，请画出相应示意图并写出△ABC最大内角的所有可能值；27. 如图，点O是等边△ABC内一点，∠AOB=110°，∠BOC=α．以OC为一边作等边三角形OCD，连接AC、AD．
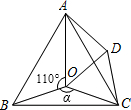(1)、求证：△BOC≌△ADC；
(2)、当α=150°时，试判断△AOD的形状，并说明理由；
(3)、探究：当a为多少度时，△AOD是等腰三角形？28.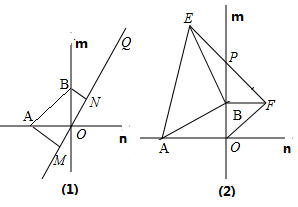
如图（1）所示，直线m⊥n，A、B分别为直线m、n上两点．
(1)、当OA=OB时，作直线OQ，过点A、B两点分别作AM⊥OQ于点M，BN⊥OQ于点N，若AM=4，BN=3，求MN的长．(2)、如图（2），OA=5，点B为直线m上方直线n上动点，分别以OB、AB为边，点B为直角顶点，在△ABO外侧作等腰直角三角形OBF和等腰直角三角形ABE，∠ABE=∠ABF=900 ， 联结EF交直线m于点P，问：当点B运动时，试猜想PB的长是否为定值，若是，请求出其值；若不是，请说明理由．