浙江省湖州市吴兴区2021届九年级上学期数学10月月考试卷

试卷更新日期：2020-10-28 类型：月考试卷

进入出卷网下载

一、选择题（共10小题，满分30分，每小题3分）

1. 下列各式中，y是x的二次函数的是（　　）

A、y＝3x﹣1 B、y＝ $\frac{1}{x^{2}}$ C、y＝3x²+x﹣1 D、y＝2x²+ $\frac{1}{x}$

查看试题解析
2. 下列说法正确的是（　　）

A、“经过有交通信号的路口遇到红灯”是必然事件 B、已知某篮球运动员投篮投中的概率为0.6，则他投10次一定可投中6次 C、投掷一枚硬币正面朝上是随机事件 D、明天太阳从东方升起是随机事件

查看试题解析
3. 抛物线y＝（x﹣3）²﹣5的顶点坐标是（）

A、（3，5） B、（﹣3，5） C、（3，﹣5） D、（﹣3，﹣5）

查看试题解析
4. 关于抛物线y＝x²﹣6x+9，下列说法错误的是（　　）

A、开口向上 B、顶点在x轴上 C、对称轴是x＝3 D、x＞3时，y随x增大而减小

查看试题解析
5. 如图，直线y₁＝mx+n和抛物线y₂＝ax²+bx+c交于A（﹣3，1）和B （1，2）两点，使得y₁＞y₂的x的取值范围是（　　）

A、x＞1 B、x＞﹣3 C、﹣3＜x＜1 D、x＞1或x＜﹣3

查看试题解析
6. 在一个不透明的盒子里有形状、大小相同的黄球2个、红球3个，从盒子里任意摸出1个球，摸到黄球的概率是（　　）

A、 $\frac{2}{5}$ B、 $\frac{3}{5}$ C、 $\frac{1}{5}$ D、 $\frac{1}{3}$

查看试题解析
7. 如图，抛物线y＝x²+2x﹣1与x轴相交于A ， B两点，与y轴交于点C ，点D在抛物线上，且CD∥AB ，则线段CD的长为（　　）

A、2 B、3 C、4 D、 $\sqrt{17}$

查看试题解析

8. 已知二次函数y＝ax²+bx+c自变量x的部分取值和对应函数值y如表：

x	…	﹣2	﹣1	0	1	2	3	…
y	…	8	3	0	﹣1	0	3	…

则在实数范围内能使得y﹣3＞0成立的x取值范围是（　　）

A、x＞3 B、x＜﹣1 C、﹣1＜x＜3 D、x＜﹣1或x＞3

查看试题解析

9. 在Rt△ABC中，∠C＝90°，BC＝a ， AC＝b ， AB＝c ，若a+b＝5，则Rt△ABC的面积S关于边长c的函数关系式为（　　）

A、S＝ $\frac{25 {-c}^{2}}{4}$ B、S＝ $\frac{25 {-c}^{2}}{2}$ C、S＝ $\frac{25 -c}{2}$ D、S＝ $\frac{25 {+c}^{2}}{4}$

查看试题解析
10. 如图，抛物线y＝﹣x²+2x+m+1（m为常数）交y轴于点A ，与x轴的一个交点在2和3之间，顶点为B ．
①抛物线y＝﹣x²+2x+m+1与直线y＝m+2有且只有一个交点；

②若点M（﹣2，y₁）、点N（ $\frac{1}{2}$ ，y₂）、点P（2，y₃）在该函数图象上，则y₁＜y₂＜y₃；

③将该抛物线向左平移2个单位，再向下平移2个单位，所得抛物线解析式为y＝﹣（x+1）²+m；

④点A关于直线x＝1的对称点为C ，点D、E分别在x轴和y轴上，当m＝1时，四边形BCDE周长的最小值为 $\sqrt{34} + \sqrt{2}$ ．

其中正确判断有（　　）

A、①②③④ B、②③④ C、①③④ D、①③

查看试题解析

二、填空题（共6小题，满分24分，每小题4分）

11. 当x＝0时，函数y＝2x²+1的值为．

查看试题解析
12. 一个不透明的袋子中装有若干个红球和6个黄球，它们除颜色外都相同，从中随机摸出一个球，记下颜色后放回，通过大量反复实验发现，摸到黄球的频率约为0.3，由此推测从这个袋中摸到红球的概率约为.

查看试题解析
13. 二次函数y＝ax²+bx+c（0≤x≤3）的图象如图所示，则y的取值范围是．

查看试题解析
14. 斐波那契螺旋线也称为“黄金螺旋线”，是根据斐波那契数列画出来的螺旋曲线，自然界中存在许多斐波那契螺旋线国案，下列四张分别画有斐波那契螺旋线图案的卡片，它们的背面完全相同．现将它们背面朝上，从中任取一张，卡片上所画图案恰好是中心对称图形的概率是．

查看试题解析
15. 如图，已知抛物线y＝ax²+bx+c与x轴交于A、B两点，顶点C的纵坐标为﹣2，现将抛物线向右平移2个单位，得到抛物线y＝a₁x²+b₁x+c₁ ，则下列结论正确的是．（写出所有正确结论的序号）

①b＞0

②a﹣b+c＜0

③阴影部分的面积为4

④若c＝﹣1，则b²＝4a ．

查看试题解析
16. 在直角坐标系xOy中，对于点P（x ， y）和Q（x ， y′）．给出如下定义：若y′＝ ${\begin{cases} y (x \geq 0) \\ - y (x < 0) \end{cases}$ ，则称点Q为点P的“可控变点”．如：点（1，2）的“可控变点”为点（1，2），点（﹣1，3）的“可控变点”为点（﹣1，﹣3）．

(1)、若点（﹣1，﹣2）是一次函数y＝x+3图象上点M的“可控变点”，则点M的坐标为．

(2)、若点P在函数y＝﹣x²+16（﹣5≤x≤a）的图象上，其“可控变点”Q的纵坐标y′的取值范围是﹣16≤y′≤16，则实数a的取值范围是．

查看试题解析

三、解答题（共8小题，满分66分）

17. 如图，将小球沿某方向击出时，小球的飞行路线是一条抛物线．如果不考虑空气阻力，小球的飞行高度h（单位：m）与飞行时间t（单位：s）之间具有函数关系h＝20t﹣5t² ．

(1)、求小球飞出1s时的飞行高度；

(2)、求小球从飞出到落地要用的时间．

查看试题解析
18. 已知二次函数y＝ax²+bx﹣3的图象经过点（1，﹣4）和（﹣1，0）．

(1)、求这个二次函数的表达式；

(2)、x在什么范围内，y随x增大而减小？该函数有最大值还是有最小值？求出这个最值．

查看试题解析
19. 新定义：[a ， b ， c]为二次函数y＝ax²+bx+c（a≠0，a ， b ， c为实数）的“图象数”，如：y＝﹣x²+2x+3的“图象数”为[﹣1，2，3]

(1)、二次函数y＝ $\frac{1}{3}$ x²﹣x﹣1的“图象数”为．

(2)、若“图象数”是[m ， m+1，m+1]的次函数的图象与x轴只有一个交点，求m的值．

查看试题解析
20. 某单位为了创建城市文明单位，准备在单位的墙（线段MN所示）外开辟一处长方形的土地进行绿化美化，除墙体外三面要用栅栏围起来，计划用栅栏50米．

(1)、不考虑墙体长度，问长方形的各边的长为多少时，长方形的面积最大？

(2)、若墙体长度为20米，问长方形面积最大是多少？

查看试题解析
21. 如图，是一座古拱桥的截面图，拱桥桥洞的上沿是抛物线形状，当水面的宽度为10m时，桥洞与水面
的最大距离是5m．

(1)、经过讨论，同学们得出三种建立平面直角坐标系的方案（如图），你选择的方案是（填方案一，方案二，或方案三），则B点坐标是，求出你所选方案中的抛物线的表达式；

(2)、因为上游水库泄洪，水面宽度变为6m，求水面上涨的高度．

查看试题解析
22. 暑期，某学校将组织部分优秀学生分别到A、B、C、D四个地方进行夏令营活动，学校按定额购买了前往四地的车票．如图1是未制作完成的车票种类和数量的条形统计图，请根据统计图回答下列问题：

(1)、若去C地的车票占全部车票的30%，则去C地的车票数量是张，补全统计图；

(2)、若学校采用随机抽取的方式分发车票，每人一张（所有车票的形状、大小、质地完全相同且充分洗匀），那么李明同学抽到去B地的概率是多少？

(3)、若有一张去A地的车票，红红和天天都想要，决定采取旋转转盘的方式来确定．其中甲转盘被分成四等份且标有数字1、2、3、4，乙转盘分成三等份且标有数字7、8、9，如图2所示．具体规定是：同时转动两个转盘，当指针指向的两个数字之和是偶数时，票给红红，否则票给天天（指针指在线上重转）．试用“列表法”或“树状图”的方法分析这个规定对双方是否公平．

查看试题解析
23. 有一家苗圃计划种植桃树和柏树，根据市场调查与预测，种植桃树的利润y₁（万元）与投资成本x（万元）满足如图1所示的二次函数y₁＝ax²；种植柏树的利润y₂（万元）与投资成本x（万元）满足如图2所示的正比例函数y₂＝kx ．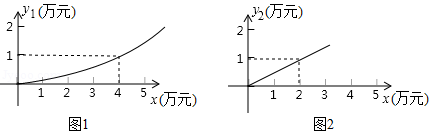

(1)、请分别直接写出利润y₁（万元）与利润y₂（万元）关于投资成本x（万元）的函数关系式；

(2)、若这家苗圃投资4万元种植桃树，投资6万元种植柏树，则可获得的总利润是多少万元？

(3)、若这家苗圃种植桃树和柏树投入总成本20万元，且桃树的投资成本不低于2万元，且不高于12万元，则苗圃最少能获得多少总利润？最多可获得多少总利润？

查看试题解析
24. 如图，函数y=-x²+bx+c的图象经过点A（m ， 0），B（0，n）两点，m ， n分别是方程x²-2x-3=0的两个实数根，且m＜n ．

(1)、求m ， n的值以及函数的解析式；

(2)、设抛物线y=-x²+bx+c与x轴的另一交点为点C ，顶点为点D ，连结BD、BC、CD ，求△BDC面积；

(3)、对于（1）中所求的函数y=-x²+bx+c ，
①当0≤x≤3时，求函数y的最大值和最小值；
②设函数y在t≤x≤t+1内的最大值为p ，最小值为q ，若p-q=3，求t的值．

查看试题解析