浙江省名校协作体2020-2021学年高二上学期数学开学考试试卷
试卷更新日期:2020-10-28 类型:开学考试
一、单选题
-
1. 已知集合 , ,则 ( )A、 B、 C、 D、2. 已知角 的顶点与原点O重合,始边与 轴的非负半轴重合,将 的终边按顺时针方向旋转 后,过点 ,则 等于( )A、 B、 C、 D、3. 下列函数中,既是偶函数,又在 上单调递增的是( )A、 B、 C、 D、4. 已知 ,则下列不等式正确的是( )A、 B、 C、 D、5. 将函数 的图象经过以下变换后可得函数 的图象,其中不正确的是( )A、向左平移 B、向右平移 C、向左平移 ,再作关于 轴对称 D、向左平移 ,再作关于 轴对称6. 若函数 的图象上存在点 ,满足不等式组 ,则实数 的取值范围为( )A、 B、 C、 D、7. 下列函数图象中,不可能是函数 的图象的是( )A、
 B、
B、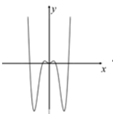 C、
C、 D、
D、 8. 已知数列 是无穷等差数列, 是其前n项和,若 存在最大值,则( )A、在 中最大的数是 B、在 中最大的数是 C、在 中最大的数是 D、在 中最大的数是9. 在 中, , , 是 的外接圆的直径,则 的取值范围是( )A、 B、 C、 D、10. 已知对任意 ,不等式 恒成立,则( )A、 B、 C、存在 ,有 D、对于任意 ,有
8. 已知数列 是无穷等差数列, 是其前n项和,若 存在最大值,则( )A、在 中最大的数是 B、在 中最大的数是 C、在 中最大的数是 D、在 中最大的数是9. 在 中, , , 是 的外接圆的直径,则 的取值范围是( )A、 B、 C、 D、10. 已知对任意 ,不等式 恒成立,则( )A、 B、 C、存在 ,有 D、对于任意 ,有二、双空题
-
11. 已知向量 ,若 ,则 ;若 ,则 =.12. 已知函数 ,则 ; 的零点为.13. 已知数列 中, , ,则 ;设数列 的前 项的和为 ,则 =.14. 已知 中,角A,B,C所对的边分别是 ,已知 , 是边 上一点,且 ,则 =; =.
三、填空题
-
15. 已知 为正实数,且 ,则 的最小值为.16. 设 ,当 取得最小值 时,函数 的最小值为.17. 已知数列 满足: , ,若正整数 使得 成立,则 .
四、解答题
-
18. 已知函数 .(1)、求 的最小正周期及 的值;(2)、若 ,求 的取值范围.19. 已知数列 是公差为正的等差数列, 是 和 的等比中项, .(1)、求 的通项公式;(2)、若 , 是数列 的前n项和,求使得 成立的最大整数n.