2020-2021学年初中数学苏科版九年级上学期期中模拟试卷B
试卷更新日期:2020-10-28 类型:期中考试
一、单选题
-
1. 若 是关于x的一元二次方程 的一个根,则 的值为( )A、2018 B、2020 C、2022 D、20242. 一元二次方程 的根的情况是( )A、有两个不等的实数根 B、有两个相等的实数根 C、无实数根 D、无法确定3. 疫情期间居民为了减少外出时间,更愿意使用 在线上买菜,某买菜 今年一月份新进册用户为200万,三月份新注册用户为338万,则二、三两个月新注册用户每月平均增长率是( )A、10% B、15% C、23% D、30%4. 已知A为⊙O外一点,若点A到⊙O上的点的最短距离为2,最长离为4,则⊙O半径为( )A、4 B、3 C、2 D、15. 如图,在⊙O中,直径CD⊥弦AB,则下列结论中正确的是( )
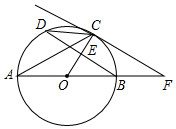
 A、AC=AB B、∠C= ∠BOD C、∠C=∠B D、∠A=∠B0D6. 如图,AB为⊙O的直径,点C,点D是⊙O上的两点,连接CA,CD,AD.若∠CAB=40°,则∠ADC的度数是( )
A、AC=AB B、∠C= ∠BOD C、∠C=∠B D、∠A=∠B0D6. 如图,AB为⊙O的直径,点C,点D是⊙O上的两点,连接CA,CD,AD.若∠CAB=40°,则∠ADC的度数是( )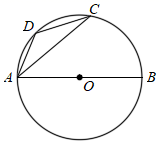 A、110° B、130° C、140° D、160°7. 学校有一块长30m,宽20m的矩形空地,计划在这块空地上划出四分之一的区域种花,小阳同学设计方案如图所示,求花带的宽度.设花带的宽度为xm,则可列方程为( )
A、110° B、130° C、140° D、160°7. 学校有一块长30m,宽20m的矩形空地,计划在这块空地上划出四分之一的区域种花,小阳同学设计方案如图所示,求花带的宽度.设花带的宽度为xm,则可列方程为( ) A、(30-x)(20-x)= ×20×30 B、(30-2x)(20-x)= ×20×30 C、30x+2×20x= ×20×30 D、(30-2x)(20-x)= ×20×308. 如图,矩形 中, , ,以 为直径的半圆与 相切,连接 . 则阴影部分的面积为( )
A、(30-x)(20-x)= ×20×30 B、(30-2x)(20-x)= ×20×30 C、30x+2×20x= ×20×30 D、(30-2x)(20-x)= ×20×308. 如图,矩形 中, , ,以 为直径的半圆与 相切,连接 . 则阴影部分的面积为( )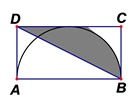 A、 B、 C、 D、9. 已知关于x的一元二次方程 与 ,下列判断错误的是( )A、若方程 有两个实数根,则方程 也有两个实数根; B、如果m是方程 的一个根,那么 是 的一个根; C、如果方程 与 有一个根相等,那么这个根是1; D、如果方程 与 有一个根相等,那么这个根是1或-1.10. 如图,AB是⊙O的直径,⊙O交BC的中点于D,DE⊥AC于E,连接AD,则下列结论:
A、 B、 C、 D、9. 已知关于x的一元二次方程 与 ,下列判断错误的是( )A、若方程 有两个实数根,则方程 也有两个实数根; B、如果m是方程 的一个根,那么 是 的一个根; C、如果方程 与 有一个根相等,那么这个根是1; D、如果方程 与 有一个根相等,那么这个根是1或-1.10. 如图,AB是⊙O的直径,⊙O交BC的中点于D,DE⊥AC于E,连接AD,则下列结论:①AD⊥BC;②∠EDA=∠B;③OA= AC;④DE是⊙O的切线,正确的个数是( )
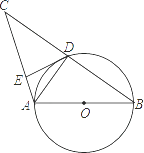 A、1 个 B、2个 C、3 个 D、4个
A、1 个 B、2个 C、3 个 D、4个二、填空题
-
11. 圆锥的底面半径为3,侧面积为 ,则这个圆锥的母线长为.12. 已知关于 的一元二次方程 有实数根,则m的取值范围是 .13. 若一元二次方程2x2﹣3x+1=0的两个实数根为x1 , x2 , 则x12+x22﹣x1•x2的值是 .14. 如图,AB为⊙O的直径,半径OA的垂直平分线交⊙O于点C,D,P为优弧AC上一点,则∠APC=°.
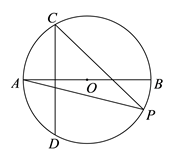 15. 如图OC是⊙O的半径,弦AB⊥OC于点D,点E在⊙O上,EB恰好经过圆心O.连接EC.若∠B=∠E,OD= ,则劣弧AB的长为 .
15. 如图OC是⊙O的半径,弦AB⊥OC于点D,点E在⊙O上,EB恰好经过圆心O.连接EC.若∠B=∠E,OD= ,则劣弧AB的长为 .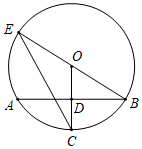 16. 已知x=1是关于x的一元二次方程x2+ax﹣2b=0的解,则代数式2a﹣4b的值为.17. 已知m是方程式x2+x﹣1=0的根,则式子m3+2m2+2019的值为.18. 如图直线 与x轴、y轴分别交于点A,B,C是 的中点,点D在直线 上,以 为直径的圆与直线 的另一交点为E,交y轴于点F,G,已知 , ,则 的长是 .
16. 已知x=1是关于x的一元二次方程x2+ax﹣2b=0的解,则代数式2a﹣4b的值为.17. 已知m是方程式x2+x﹣1=0的根,则式子m3+2m2+2019的值为.18. 如图直线 与x轴、y轴分别交于点A,B,C是 的中点,点D在直线 上,以 为直径的圆与直线 的另一交点为E,交y轴于点F,G,已知 , ,则 的长是 .
三、综合题
-
19. 已知:如图,圆O是△ABC的外接圆,AO平分∠BAC .
 (1)、求证:△ABC是等腰三角形;(2)、当OA=4,AB=6,求边BC的长.20. 已知关于x的方程 .(1)、若 是该方程的根,求k的值;(2)、若该方程有两个不相等的实数根,求k的取值范围.21. 已知:如图所示.在△ABC中,∠B=90°,AB=5cm , BC=7cm . 点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,当其中一点达到终点后,另外一点也随之停止运动.
(1)、求证:△ABC是等腰三角形;(2)、当OA=4,AB=6,求边BC的长.20. 已知关于x的方程 .(1)、若 是该方程的根,求k的值;(2)、若该方程有两个不相等的实数根,求k的取值范围.21. 已知:如图所示.在△ABC中,∠B=90°,AB=5cm , BC=7cm . 点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,当其中一点达到终点后,另外一点也随之停止运动. (1)、如果P , Q分别从A , B同时出发,那么几秒后,△PBQ的面积等于4cm2?(2)、如果P , Q分别从A , B同时出发,那么几秒后,PQ的长度等于5cm?(3)、在(1)中,△PQB的面积能否等于7cm2?说明理由.22. 一商店销售某种商品,平均每天可售出20件,每件盈利40元,为了扩大销售,增加盈利,该店采取了降价措施,在每件盈利不少于25元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出2件.(1)、若降价a元,则平均每天销售数量为件.(用含a的代数式表示)(2)、当每件商品降价多少元时,该商店每天销售利润为1200元.23. 如图,在△ABC中,AB=AC,O是边AC上的点,以OC为半径的圆分别交边BC、AC于点D、E,过点D作DF⊥AB于点F.
(1)、如果P , Q分别从A , B同时出发,那么几秒后,△PBQ的面积等于4cm2?(2)、如果P , Q分别从A , B同时出发,那么几秒后,PQ的长度等于5cm?(3)、在(1)中,△PQB的面积能否等于7cm2?说明理由.22. 一商店销售某种商品,平均每天可售出20件,每件盈利40元,为了扩大销售,增加盈利,该店采取了降价措施,在每件盈利不少于25元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出2件.(1)、若降价a元,则平均每天销售数量为件.(用含a的代数式表示)(2)、当每件商品降价多少元时,该商店每天销售利润为1200元.23. 如图,在△ABC中,AB=AC,O是边AC上的点,以OC为半径的圆分别交边BC、AC于点D、E,过点D作DF⊥AB于点F. (1)、求证:直线DF是⊙O的切线;(2)、若OC=1,∠A=45°,求劣弧DE的长.24. 如图,以矩形ABCD的边CD为直径作⊙O,点E是AB 的中点,连接CE交⊙O于点F,连接AF并延长交BC于点H.
(1)、求证:直线DF是⊙O的切线;(2)、若OC=1,∠A=45°,求劣弧DE的长.24. 如图,以矩形ABCD的边CD为直径作⊙O,点E是AB 的中点,连接CE交⊙O于点F,连接AF并延长交BC于点H. (1)、若连接AO,试判断四边形AECO的形状,并说明理由;(2)、求证:AH是⊙O的切线;(3)、若AB=6,CH=2,则AH的长为.
(1)、若连接AO,试判断四边形AECO的形状,并说明理由;(2)、求证:AH是⊙O的切线;(3)、若AB=6,CH=2,则AH的长为.