2020-2021学年初中数学苏科版九年级上学期期中模拟试卷A
试卷更新日期:2020-10-28 类型:期中考试
一、单选题
-
1. 下列方程中,关于 的一元二次方程是( )A、 B、 C、 D、2. 已知关于x的一元二次方程x2+bx-1=0,则下列关于该方程根的判断,正确的是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、实数根的个数与实数b的取值有关3. 如图,在⊙O中,半径r=10,弦AB=16,P是弦AB上的动点(不含端点A,B),若线段OP长为正整数,则点P的个数有( )
 A、4个 B、5个 C、6个 D、7个4. 如图,四边形 内接于 ,连接 .若 , ,则 的度数是( )
A、4个 B、5个 C、6个 D、7个4. 如图,四边形 内接于 ,连接 .若 , ,则 的度数是( )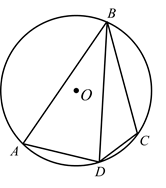 A、125° B、130° C、135° D、140°5. 如图是一个废弃的扇形统计图,小明同学利用它的阴影部分制作一个圆锥,则这个圆锥的底面半径是( )
A、125° B、130° C、135° D、140°5. 如图是一个废弃的扇形统计图,小明同学利用它的阴影部分制作一个圆锥,则这个圆锥的底面半径是( )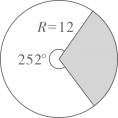 A、3.6 B、1.8 C、3 D、66. 如图,⊙O是正五边形ABCDE的外接圆,点P是 的一点,则∠CPD的度数是( )
A、3.6 B、1.8 C、3 D、66. 如图,⊙O是正五边形ABCDE的外接圆,点P是 的一点,则∠CPD的度数是( )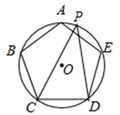 A、30° B、36° C、45° D、72°7. 在元旦庆祝活动中,参加活动的同学互赠贺卡,共送贺卡90张,则参加活动的有( )人.
A、30° B、36° C、45° D、72°7. 在元旦庆祝活动中,参加活动的同学互赠贺卡,共送贺卡90张,则参加活动的有( )人.
A、9 B、10 C、12 D、158. 如图,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型,若圆的半径为r,扇形的圆心角等于120°,则围成的圆锥模型的高为( )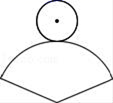 A、r B、2 r C、 r D、3r9. 规定:如果关于x的一元二次方程ax2+bx+c=0(a≠0)有两个实数根,且其中一个根是另一个根的2倍,则称这样的方程为“倍根方程”现有下列结论
A、r B、2 r C、 r D、3r9. 规定:如果关于x的一元二次方程ax2+bx+c=0(a≠0)有两个实数根,且其中一个根是另一个根的2倍,则称这样的方程为“倍根方程”现有下列结论①方程x2+2x﹣8=0是倍根方程;②若关于x的方程x2+ax+2=0是倍根方程,则a=±3;③若(x﹣3)(mx﹣n)=0是倍根方程,则n=6m或3n=2m;④若点(m,n)在反比例函数y= 的图象上,则关于x的方程mx2﹣3x+n=0是倍根方程.上述结论中正确的有( )
A、② B、①③ C、②③④ D、②④10. 如图,在△ABC中,BC=4,以点A为圆心,2为半径的⊙A与BC相切于点D,交AB于点E,交AC于点F.P是⊙A上一点,且∠EPF=40°,则图中阴影部分的面积是( ) A、4- B、4- C、8- D、8-
A、4- B、4- C、8- D、8-二、填空题
-
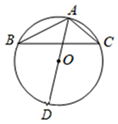
11. 在半径为1的⊙O中,弦AB=1,则弧AB的长为.12. 若方程 的两个根分别为 和 ,则 =.13. 如图, 为 的外接圆 的直径,如果 ,那么 .
 14. 已知三角形两边的长分别是2和5,第三边的长是方程 的根,则这个三角形的周长是15. 已知关于x的方程x2+kx-2=0的一个根是x=2,则另外一个根为 .16. 如图,在扇形OAB中,点C在 上,∠AOB=90°,∠ABC=30°,AD⊥BC于点D,连接AC,若OA=2,则图中阴影部分的面积为 。
14. 已知三角形两边的长分别是2和5,第三边的长是方程 的根,则这个三角形的周长是15. 已知关于x的方程x2+kx-2=0的一个根是x=2,则另外一个根为 .16. 如图,在扇形OAB中,点C在 上,∠AOB=90°,∠ABC=30°,AD⊥BC于点D,连接AC,若OA=2,则图中阴影部分的面积为 。 17. 一个两位数,十位上的数字比个位上的数字的平方少9.如果把十位上的数字与个位上的数字对调,得到的两位数比原来的两位数小27,则原来的两位数是18. 如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点.若⊙O的半径为7,则GE+FH的最大值为.
17. 一个两位数,十位上的数字比个位上的数字的平方少9.如果把十位上的数字与个位上的数字对调,得到的两位数比原来的两位数小27,则原来的两位数是18. 如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点.若⊙O的半径为7,则GE+FH的最大值为.
三、解答题
-
19.(1)、用配方法解方程:x2﹣4x﹣1=0(2)、解方程:(2x+1)2=﹣3(2x+1)20. 若关于x的一元二次方程x2﹣3x+a﹣2=0有实数根.(1)、求a的取值范围;(2)、当a为符合条件的最大整数,求此时方程的解.21. 如图,已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D.
 (1)、求证:AC=BD;(2)、若大圆的半径R=10,小圆半径r=8,且圆心O到直线AB的距离为6,求AC的长
(1)、求证:AC=BD;(2)、若大圆的半径R=10,小圆半径r=8,且圆心O到直线AB的距离为6,求AC的长
22. 某农场要建一个饲养场(长方形ABCD),饲养场的一面靠墙(墙最大可用长度为27米),另三边用木栏围成,中间也用木栏隔开,分成两个场地,并在如图所示的三处各留1米宽的门(不用木栏),建成后木栏总长57米,设饲养场(长方形ABCD)的宽为a米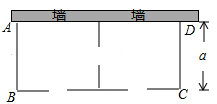 (1)、饲养场的长为米(用含a的代数式表示)(2)、若饲养场的面积为288 ,求a的值23. 2020年突如其来的新型冠状病毒疫情,给生鲜电商带来了意想不到的流量和机遇,据统计某生鲜电商平台1月份的销售额是1440万元,3月份的销售额是2250万元.(1)、若该平台1月份到3月份的月平均增长率都相同,求月平均增长率是多少?(2)、市场调查发现,某水果在“盒马鲜生”平台上的售价为20元/千克时,每天能销售200千克,售价每降价2元,每天可多售出100千克,为了推广宣传,商家决定降价促销,同时尽量减少库存,已知该水果的成本价为12元/千克,若使销售该水果每天获利1750元,则售价应降低多少元?24. 如图,在 中, ,以 为直径的 交 于点D,过点D作 ,垂足为点E.
(1)、饲养场的长为米(用含a的代数式表示)(2)、若饲养场的面积为288 ,求a的值23. 2020年突如其来的新型冠状病毒疫情,给生鲜电商带来了意想不到的流量和机遇,据统计某生鲜电商平台1月份的销售额是1440万元,3月份的销售额是2250万元.(1)、若该平台1月份到3月份的月平均增长率都相同,求月平均增长率是多少?(2)、市场调查发现,某水果在“盒马鲜生”平台上的售价为20元/千克时,每天能销售200千克,售价每降价2元,每天可多售出100千克,为了推广宣传,商家决定降价促销,同时尽量减少库存,已知该水果的成本价为12元/千克,若使销售该水果每天获利1750元,则售价应降低多少元?24. 如图,在 中, ,以 为直径的 交 于点D,过点D作 ,垂足为点E.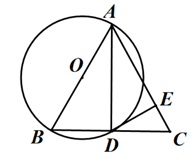 (1)、求证: ;(2)、判断直线 与 的位置关系,并说明理由.25. 定义:若关于x的一元二次方程 的两个实数根为 ,分别以 为横坐标和纵坐标得到点M ,则称点M为该一元二次方程的衍生点(1)、若一元二次方程为 ,请直接写出该方程的衍生点M的坐标为(2)、若关于x的一元二次方程为
(1)、求证: ;(2)、判断直线 与 的位置关系,并说明理由.25. 定义:若关于x的一元二次方程 的两个实数根为 ,分别以 为横坐标和纵坐标得到点M ,则称点M为该一元二次方程的衍生点(1)、若一元二次方程为 ,请直接写出该方程的衍生点M的坐标为(2)、若关于x的一元二次方程为①求出该方程的衍生点M的坐标;
②直线 :y=x+5与x轴交于点A,直线 过点B(1,0),且 与 相交于点C( 1,4),若由①得到的点M在 的内部,求 的取值范围;
(3)、是否存在b,c,使得不论k(k≠0)为何值,关于x的方程 的行生点M始终在直线 的图象?若有,请求出b,c的值;若没有,请说明理由26. 如图,四边形ABCD内接于⊙O,AC为直径,AC和BD交于点E,AB=BC.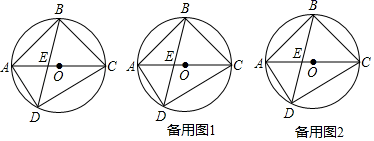 (1)、求∠ADB的度数;(2)、过B作AD的平行线,交AC于F,试判断线段EA,CF,EF之间满足的等量关系,并说明理由;(3)、在(2)条件下过E,F分别作AB,BC的垂线,垂足分别为G,H,连接GH,交BO于M,若AG=3,S四边形AGMO:S四边形CHMO=8:9,求⊙O的半径.
(1)、求∠ADB的度数;(2)、过B作AD的平行线,交AC于F,试判断线段EA,CF,EF之间满足的等量关系,并说明理由;(3)、在(2)条件下过E,F分别作AB,BC的垂线,垂足分别为G,H,连接GH,交BO于M,若AG=3,S四边形AGMO:S四边形CHMO=8:9,求⊙O的半径.