上海市宝山区2020-2021学年九年级上学期数学第一次月考试卷

试卷更新日期：2020-10-27 类型：月考试卷

进入出卷网下载

一、选择题

1. 已知线段b是线段a、c的比例中项，a=3，c=2，那么b的长度等于（）

A、± $\sqrt{6}$ B、6 C、 $\sqrt{6}$ D、 $\frac{16}{9}$

查看试题解析
2. 已知x：y=2：3，下列等式中正确的是（）

A、(x-y)：y=1：3 B、(x-y)：y=2：1 C、(x-y)：y=-1：3 D、(x-y)：y=-1：2

查看试题解析
3. 如果点C是线段AB的黄金分割点，那么下列线段比中比值不可为 $\frac{\sqrt{5} - 1}{2}$ 的是（）

A、 $\frac{A C}{B C}$ B、 $\frac{B C}{A C}$ C、 $\frac{A B}{B C}$ D、 $\frac{A C}{A B}$

查看试题解析
4. 下列命题中的真命题是（）

A、两个直角三角形都相似 B、若一个直角三角形的两条边和另一个直角三角形的两条边成比例，则这两个直角三角形相似 C、两个等腰三角形都相似 D、两个等腰直角三角形都相似

查看试题解析
5. 如图，△ABC中，G是BC中点，E是AG中点，CE的延长线交AB于D，则 $\frac{E C}{D E}$ 的值为（）

A、2 B、3 C、 $\frac{1}{3}$ D、 $\frac{1}{2}$

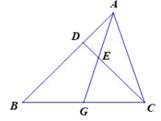查看试题解析
6. 有以下命题：．
①如果线段d是线段a、b、c的第四比例项，则有 $\frac{a}{b} = \frac{c}{d}$

②如果点C是线段AB的中点，那么AC是AB、BC的比例中项

③如果点C是线段AB的黄金分割点，且AC>BC，那么AC是AB、BC的比例中项

④如果点C是线段AB的黄金分割点，且AC>BC，且AB=2，则AC= $\sqrt{5}$ -1

其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

7. 已知 $\frac{x}{5} = \frac{y}{3} = \frac{z}{4}$ ，则 $\frac{2 x + y - z}{x + 3 y + z}$ =。

查看试题解析
8. 如图，G为△ABC的重心，GN∥AC交BC于N，那么GN：AC=。

查看试题解析
9. 如图，AB∥CD，AD与BC交于点O，若 $\frac{O C}{O D} = \frac{5}{3}$ ，则 $\frac{A O}{B O}$ =。

查看试题解析
10. 两个相似三角形对应高的比为2：3，且已知这两个三角形的周长差为4，则较小的三角形的周长为。

查看试题解析
11. 当两个相似三角形的相似比为时，这两个相似三角形-定是-对全等三角形。

查看试题解析
12. 如图，△ABC中，D、F在AB边上，E、G在AC边上，DE∥FG∥BC，且AD：DF：FB=3：2：1，若AG=15，则EC的长为。

查看试题解析
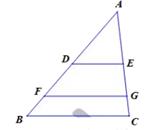13. 如图，△ABC的两条中线AD、BE相交于点G，如果S_△ABG=2，那么S△ABC=。

查看试题解析
14. 如图，梯形ABCD中，点E、F分别在边AB、DC上，AD∥BC∥EF，BE：EA=1：2，若AD=2，BC=5，则EF=。

查看试题解析
15. 如图，电灯P在横杆AB的正上方，AB在灯光下的影子为CD，AB∥CD，AB=2cm，CD=5cm，点P到CD的距离是3cm，则点P到AB的距离是。

查看试题解析
16. 如图，AB、CD都是BD的垂线，AB=4，CD=6，BD=14，P是BD上一点，联结AP、CP，所得两个三角形相似，则BP的长是。

查看试题解析
17. 在Rt△ABC中，∠BAC=90°，AB=3，M为边BC上的点，联结AM(如图所示)，如果将△ABM沿直线AM翻折后，点B恰好落在边AC的中点处，那么点M到AC的距离是。

查看试题解析
18. 如图，将正方形纸片ABCD对折，使AB与CD重合，折痕为EF，展开后再折叠一次，使点C与点E重合，折痕为GH，点B的对应点为点M，EM交AB于N，若AD=2，则MN=。

查看试题解析

三、解答题。

19. 已知 $\frac{a}{3} = \frac{b}{2}$ ≠0，求代数式 $\frac{2 a - b}{a^{2} - 4 b^{2}}$ ·(a+2b)的值。

查看试题解析
20. 如图，已知 $\frac{D E}{B C} = \frac{A D}{A B} = \frac{A E}{A C}$ ，

求证：

(1)、∠DAB=∠EAC；

(2)、DB·AC=AB·EC

查看试题解析
21. 如图，正方形DEFG的边EF在△ABC的边上，顶点D、G分别在边AB、AC上，已知△ABC的边BC=15，高AH=10，求：正方形DEFG的边长和面积。

查看试题解析
22. 如图，

点D、E分别在△ABC的边AB、AC上，DE∥BC

(1)、若S_△ADE=2，S△BCE=7.5，求S_△BDE；

(2)、若S_△BDE=m，S_△BCE=n，求S_△ABC(用m、n表示)

查看试题解析
23. 如图，四边形ABCD中，AD=CD，∠DAB=∠ACB=90°，过点D作DE⊥AC，垂足为F，DE与AB相交于点E

(1)、求证：AB·AF=CB·CD

(2)、已知AB=15cm，BC=9cm，P是射线DE上的动点，设DP=xcm(x> 0)，四边形BCDP的面积为ycm²
①求y关于x的函数关系式；②当x为何值时，△PBC的周长最小，并求出此时y的值。

查看试题解析
24. 如图，直角梯形OABC的直角顶点O是坐标原点，边OA、OC分别在x轴、y轴的正半轴上，OA∥BC，D是BC上一点，BD= $\frac{1}{4}$ OA= $\sqrt{2}$ ，AB=3，∠OAB=45°，E、F分别是线段OA、AB上的两动点，且始终保持∠DEF=45°。

(1)、直接写出D点的坐标；

(2)、设OE=x．AF=y，试确定y与x之间的函数关系；

(3)、当△AEF是等腰三角形时，将△AEF沿EF折叠，得到△A'EF，求△A'EF与五边形OEFBC重叠部分的面积

查看试题解析
25. 已知∠ABC=90°，AB=2，BC=3，AD∥BC，P为线段BD上的动点，点Q在射线AB上，且满足 $\frac{P Q}{P C} = \frac{A Q}{A B}$ (如图1所示)

(1)、当AD=2，且点Q与点B重合时(如图2所示)，求线段PC的长；

(2)、在图1中，联结AP，当AD= $\frac{3}{2}$ ，且点Q在线段AB上时，设点B、Q之间的距离为x， $\frac{S_{△ A P Q}}{S_{△ P B C}}$ =y，其中S_△APQ表示S_△APQ的面积，S_△PBC表示△PBC的面积，求y关于x的函数关系式，并写出函数定义域；

(3)、当AD<AB，且点Q在线段AB的延长线上时(如图3所示)，求∠QPC的大小

查看试题解析