黑龙江省哈尔滨市香坊区2020-2021学年九年级上学期数学第一次月考试卷
试卷更新日期：2020-10-27 类型：月考试卷
一、选择题(每题3分，共计30分)
-
1. 某日的最高气温为2℃ ，最低气温为-8℃，则这一天的最高气温比最低气温高（ ）A、-10℃ B、-6℃ C、6℃ D、10℃2. 用科学记数法表示6250000正确的是（ ）A、6.25×106 B、6.25×105 C、625×104 D、0.625×1073. 下列运算一定正确的是（ ）A、a2+a3=a5 B、4a-5a=-a C、2a-2= D、a10÷a2=a54. 下列图形中，不是轴对称图形的是（ ）A、
B、
C、
D、
5. 如果下列各组数是三角形的三边，那么不能组成直角三角形的一组数是（ ）A、2，3，4 B、3，4，5 C、6，8，10 D、5，12，136. 一次函数y=-5x+3的图象经过的象限是（ ）
A、一，二，三 B、二，三，四 C、一，二，四 D、一，三，四7. 如果关于x的一元二次方程kx2-6x+9=0有两个不相等的实数根，那么k的取值范围是（ ）A、k<1 B、k≠0 C、k>1 D、k<1且k≠08. 如图，矩形ABCD中，点E在边AB上，将矩形ABCD沿直线DE折叠，点A恰好落在边BC的点F处．若AE=5，BF=3，则CD的长是（ ）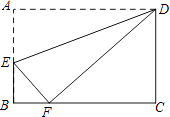
A、7 B、8 C、9 D、109. 下列四个命题中的假命题是（ ）A、对角线互相垂直的平行四边形是菱形 B、对角线相等的平行四边形是矩形 C、对角线互相垂直平分且相等的四边形是正方形： D、对角线相等的四边形是平行四边形10. 甲、乙两人在笔直的公路上同起点、同终点、同方向各自匀速步行2400米，先到终点的人原地休息．已知甲先出发4分钟，在整个步行过程中，甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示，下列结论中正确的有（ ）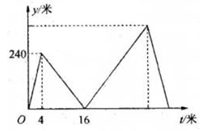
①甲步行的速度为60米/分；
②乙走完全程用了32分钟；
③乙用16分钟追上甲；
④乙到达终点时，甲离终点还有300米．
A、1个 B、2个 C、3个 D、4个二、填空题(每小题3分，共计30分)
-
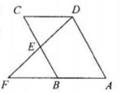
11. 计算： =。12. 函数y= 中，自变量x的取值范围是。13. 把多项式2mx2-8m分解因式的结果是。14. 一元二次方程x2-x-6=0的根是。15. 在直角坐标系中，点P(2，3)到原点的距离是。16. 如图，在四边形ABCD中，E是BC边中点，连接DE并延长，交AB的延长线于F，AB=BF，添加一个条件，使四边形ABCD是平行四边形，你添加的条件是 。
17. 某商品的原价为60元，如果经过两次降价(每次降价的百分率都相同)后价格为48.6元，那么该商品每次的降价率是。18. 要把直线y=3x-2向上平移，使其图象经过点(2，10)，需要向上平移个单位。19. 在△ABC中，∠B=30°，AB=8，AC=2 ，则BC的长为。20. 如图，在四边形BCDE中，BC⊥CD，DE⊥CD，AB⊥AE，垂足分别为C，D，A，BC≠AC，点M，N，F分别为AB，AE，BE的中点，连接MN，MF，NF。当BC=4，DE=5，∠FMN=45°时，则BE的长为。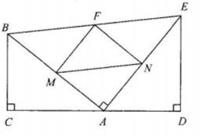
三、解答题(其中21~22题各7分，23~24题各8分，25~27题各10分，共计60分)
-
21. 先化简再求代数式的值： ，其中x= +1。22. 如图，在每个小正方形的边长为1的方格纸中有线段AB和CD，点A、B、C、D均在小正方形的顶点上。
⑴在方格纸中画出菱形ABEF，点E、F均在小正方形的顶点上，且菱形的面积为20；
⑵在方格纸中画出CD为斜边的等腰直角△CGD，点G在正方形的顶点上；
⑶在(1)(2)条件下，连接EG，请直接写出EG的长。
23. 如图，在矩形ABCD中，E是BC边上的点，AE=BC ，DF⊥AE，垂足为F，连接DE。
(1)、求证：AB=DF；(2)、若CE=1，AF=3，求DF的长。24. 如图，在△AFC中，∠FAC=45°，FE⊥AC于点E，在EF上取一点B，连接AB、BC，使得AB=FC，过点A作AD⊥AF，且AD=BC，连接CD。
(1)、如图1，求证：四边形ABCD是平行四边形；(2)、如图2，若AB平分∠FAC，延长FE交CD于点H，请直接写出与∠ABE相等的角。25. 某服装店到厂家选购A、B两种品牌的儿童服装，每套A品牌服装进价比B品牌服装每套进价多25元，已知用2000元购进A种服装的数量是用750元购进B种服装数量的2倍。(1)、求A、B两种品牌服装每套进价分别为多少元？(2)、若A品牌服装每套售价为130元，B品牌服装每套售价为95元，服装店老板决定，购进B品牌服装的数量比购进A品牌服装的数量的2倍还多4套，两种服装全部售出后，要使总利润不少于1200元，则最少购进A品牌的服装多少套？26. 矩形ABCD中，M、N为边AD上两点，连接BM、CN，MN=BM=CN，∠BMD=120°。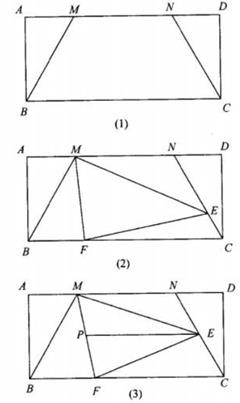
(1)、如图1，求证：AM=DN；(2)、如图2，点E、F分别在NC、BC上，∠FME=60°，求证：EF"= BF+NE；(3)、如图3，在(2)的条件下，过E作EP∥BC交MF于P，2MN=3BF，EP=7，求CE的长。27. 在平面直角坐标系中，直线y= x+b(b>0)交x轴于点A，交y轴于点B，AB=10。
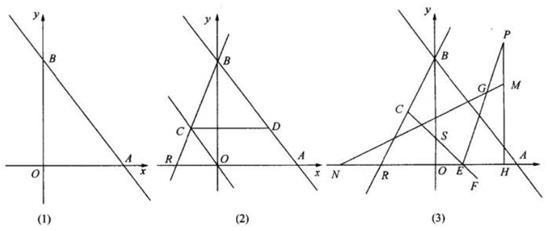(1)、如图1，求b的值；(2)、如图2，经过点B的直线y=(n+4)x+b(-4<n<0)与直线y=nx交于点C，与x轴交于点R，CD∥OA，交AB于点D，设线段CD长为d，求d与n的函数关系式；(3)、如图3，在(2)的条件下，点F在第四象限，CF交OA于点E、交0B于点S，点P在第一象限，PH⊥OA，点N在x轴上，点M在PH上，MN交PE于点G，∠EGN=45°，PH=EN，过点E作EQ⊥CF，交PH于点Q，连接BF、RQ，BF交x轴于点V，若C为BR中点，EQ=EF+2 = PM，∠ERQ=∠ABF，求点V的坐标。