安徽省巢湖市2020-2021学年九年级上学期数学第一次月考试卷
试卷更新日期:2020-10-27 类型:月考试卷
一、 选择题(本题共10小题,每小题4分,满分40分,)
-
1. 在下列函数关系式中,y是x的二次函数的是( )A、y=x+2 B、y= C、y=x2+2 D、y=2(x+3)2-2x22. 将一元二次方程x2+x=1化成一般形式后,一次项系数和常数项可能是( )A、-1,0 B、1,1 C、-1,-1 D、1,-13. 抛物线y= x2的顶点坐标是( )A、(0, ) B、(0,0) C、(0, ) D、(1, )4. 已知x=1是一元二次方程x2+kx-3=0的一个根,则k的值为( )A、2 B、-2 C、3 D、-35. 一元二次方程x2-x=2020的根的情况为( )A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根6. 将抛物线y= x2-6x+21向左平移2个单位后,再向上平移2个单位,得到新抛物线的解析式为( )A、y= (x-8)2+5 B、y= (x-4)2+5 C、y= (x-8)2+3 D、y= (x-4)2+37. 如图,在一块长为20m,宽为12m的矩形ABCD空地内修建四条宽度相等,且与矩形各边垂直的道路,四条道路围成的中间部分恰好是一个正方形,且边长是道路宽的2倍,道路占地总面积为40m2 , 设道路宽为xm,则以下方程正确的是( )
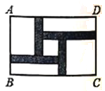 A、x(64-8x)=40 B、x(32+8x)=40 C、x(64-4x)=40 D、x(32+4x)=408. 在同一坐标系中,二次函数y=ax2+b的图象与一次函数y=bx +a的图象可能是( )A、
A、x(64-8x)=40 B、x(32+8x)=40 C、x(64-4x)=40 D、x(32+4x)=408. 在同一坐标系中,二次函数y=ax2+b的图象与一次函数y=bx +a的图象可能是( )A、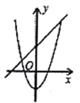 B、
B、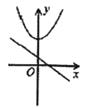 C、
C、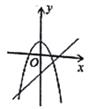 D、
D、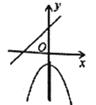 9. 已知二次函数y=a(x-2)2的图象经过点A,且当x<2时,y随x的增大而减小,则点A的坐标可以是( )A、(-1,-1) B、(0,2) C、(1,-2) D、(3,-4)10. 抛物线y=ax2+bx+c(a≠0)的部分图象如图所示,与x轴的一个交点坐标为(4,0),抛物线的对称轴是直线x=1。下列结论中:①abc>0;②2a+b=0;③4a-2b+c=0;④若点M(m,n)在该抛物线上,则am2+bm+c≤a+b+c,其中正确的个数是( )
9. 已知二次函数y=a(x-2)2的图象经过点A,且当x<2时,y随x的增大而减小,则点A的坐标可以是( )A、(-1,-1) B、(0,2) C、(1,-2) D、(3,-4)10. 抛物线y=ax2+bx+c(a≠0)的部分图象如图所示,与x轴的一个交点坐标为(4,0),抛物线的对称轴是直线x=1。下列结论中:①abc>0;②2a+b=0;③4a-2b+c=0;④若点M(m,n)在该抛物线上,则am2+bm+c≤a+b+c,其中正确的个数是( )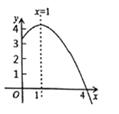 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、选择题(本题共4小题,每小题5分,满分20分)
-
11. 方程(x-1)(x-3)=0的解为。12. 若(2,5),(4,5)是抛物线y=ax2+bx+c上的两个点,则它的对称轴是直线。13. 今年国庆和中秋正好是同一天,某班数学兴趣小组的同学用互送贺卡庆贺,已知共送出贺卡132张,那么兴趣小组有学生名。14. 在△ABC中,∠ACB=90°,∠A=30°,AB=16,点P是斜边AB上一点,过点P作PQ⊥AB, 垂足为P,交边AC(或边CB)于点Q,设AP=x,当△APQ的面积为14 时,x的值为。
三、(本题共2小题,每小题8分,满分16分)
-
15. 解方程:(x-1)2=416. 已知抛物线的顶点为(2,3),且经过点(3,1),求此抛物线对应的函数解析式。
四、(本题共2小题,每题8分,满分16分)
-
17. 已知:关于x的一元二次方程:x2-6x+m=0(1)、当m=0时,求原方程的解:(2)、若方程有一个实数根为3- ,求方程另一根及m的值。18. 如图,直线y=-x+2与抛物线y=ax2交于A,B两点,点A坐标为(1,1)。
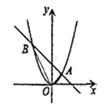 (1)、水抛物线的函数表达式:(2)、连结OA,OB,求△AOB的面积。
(1)、水抛物线的函数表达式:(2)、连结OA,OB,求△AOB的面积。五、(本题共2小题,每题10分,满分20分)
-
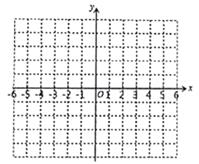
19. 已知抛物线y=-x2+2x+2(1)、该抛物线的对称轴是直线 , 顶点坐标为;(2)、填写下表,并在如图的直角坐标系内描点画出该抛物线。
x
…
-1
1
3
…
y
…
2
2
-1
…
 (3)、若A(x1 , y1),B(x2 , y1),C(I,y3)为抛物线y=-x2+2x+2上的三点,且x1<x2<1,则y1 , y2 , y3的大小关系是。20. 已知关于x的一元二次方程mx2-(2m-2)x+m-2=0(m≠0)(1)、求证:方程总有两个不相等的实数根;(2)、若方程的两个实数根都是整数,求整数m的值。
(3)、若A(x1 , y1),B(x2 , y1),C(I,y3)为抛物线y=-x2+2x+2上的三点,且x1<x2<1,则y1 , y2 , y3的大小关系是。20. 已知关于x的一元二次方程mx2-(2m-2)x+m-2=0(m≠0)(1)、求证:方程总有两个不相等的实数根;(2)、若方程的两个实数根都是整数,求整数m的值。六、(本题满分12分)
-
21. 某商场今年年初以每件25元购进一批商品.当商品售价为40元时,三月份销售128件,四、五月份该商品的销售量持续走高,在售价不变的前据下,五月份的销量达到200件。(1)、假设四、五两个月销售量的月平均增长率不变,求四、五两个月销售最的月平均增长率;(2)、从六月起,商场采用降价促销方式回馈顾客,经调查发现,该商品每降1元,销售量增加5件,当商品降价多少元时,商场可获利2250元?
七、(本题满分12分)
-
22. 有一辆宽为2m的货车(如图①),要通过一条抛物线形隧道(如图②),为确保车辆安全通行,规定货车车顶左右两侧离隧道内壁的垂直高度至少为0.5m。已知隧道的跨度AB为8m,拱高为4m。
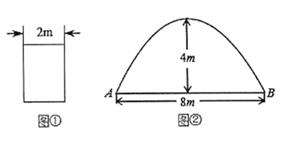 (1)、若隧道为单车道,货车高为3.2m,该货车能否安全通行?为什么?(2)、若隧道为双车道,且两车道之间有0.4m的阴离带,通过计算说明该货车能够通行的最大安全限高。
(1)、若隧道为单车道,货车高为3.2m,该货车能否安全通行?为什么?(2)、若隧道为双车道,且两车道之间有0.4m的阴离带,通过计算说明该货车能够通行的最大安全限高。八、(本题满分14分)
-
23. 如图是证明勾股定理时用到的一个图形,a,b,c是Rt△ABC和Rt△BED的边长,显然AE= c,我们把关于x的一元二次方程ax2+ cx+b=0称为“弦系一元二次方程”。
请解决下列问题:
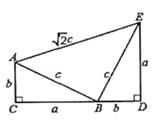 (1)、①方程 x2+ x+ =0是不是“弦系一元二次方程”: (填“是”或“否”):
(1)、①方程 x2+ x+ =0是不是“弦系一元二次方程”: (填“是”或“否”):②写出一个“弦系一元二次方程”:;
(2)、求证:关于x的“弦系一元二次方程”ax2+ cx+b=0必有实数根;(3)、当a>b时,直接写出关于x的“弦系一元二次方程”ax2+ cx+b=0的求根公式:x1= , x2= 。(4)、若x=-1是“弦系一元二次方程”ax2+ cx+b=0的一个根,且四边形ACDE的周长是6 ,求△MBC面积。
-
-