初中数学苏科版九年级上学期期中复习专题 弧长的计算
试卷更新日期:2020-10-27 类型:复习试卷
一、单选题
-
1. 如图,有一块半径为1m,圆心角为 的扇形铁皮,要把它做成一个圆锥形容器(接缝忽略不计),那么这个圆锥形容器的高为( ).
 A、 B、 C、 D、2. 已知一扇形的圆心角为 ,半径为5,则以此扇形为侧面的圆锥的底面圆的周长为( )A、 B、 C、 D、3. 如图,菱形ABCD中,∠B=70°,AB=3,以AD为直径的⊙O交CD于点E,则弧DE的长为( )
A、 B、 C、 D、2. 已知一扇形的圆心角为 ,半径为5,则以此扇形为侧面的圆锥的底面圆的周长为( )A、 B、 C、 D、3. 如图,菱形ABCD中,∠B=70°,AB=3,以AD为直径的⊙O交CD于点E,则弧DE的长为( ) A、 π B、 π C、 π D、 π4. 如图,线段AB经过⊙O的圆心,AC,BD分别与⊙O相切于点C,D.若AC=BD=4,∠A=45°,则 的长度为( )
A、 π B、 π C、 π D、 π4. 如图,线段AB经过⊙O的圆心,AC,BD分别与⊙O相切于点C,D.若AC=BD=4,∠A=45°,则 的长度为( )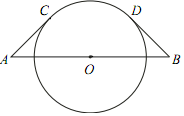 A、π B、2π C、2 π D、4π5. 如图,将矩形ABCD绕着点A逆时针旋转得到矩形AEFG,点B的对应点E落在边CD上,且DE=EF,若AD= ,则弧CF的长为( )
A、π B、2π C、2 π D、4π5. 如图,将矩形ABCD绕着点A逆时针旋转得到矩形AEFG,点B的对应点E落在边CD上,且DE=EF,若AD= ,则弧CF的长为( ) A、 B、 C、 D、π6. 如图,AB为⊙O的直径,AB=30,点C在⊙O上,∠A=24°,则 的长为( )
A、 B、 C、 D、π6. 如图,AB为⊙O的直径,AB=30,点C在⊙O上,∠A=24°,则 的长为( )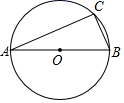 A、9π B、10π C、11π D、12π7. 如图,将等边△ABC的边AC逐渐变成以B为圆心、BA为半径的 ,长度不变,AB、BC的长度也不变,则∠ABC的度数大小由60°变为( )
A、9π B、10π C、11π D、12π7. 如图,将等边△ABC的边AC逐渐变成以B为圆心、BA为半径的 ,长度不变,AB、BC的长度也不变,则∠ABC的度数大小由60°变为( )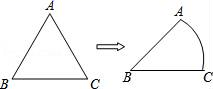 A、( )° B、( )° C、( )° D、( )°8. 一段圆弧的半径是12,弧长是 ,则这段圆弧所对的圆心角是( )A、 B、 C、 D、9. 如图,在 中, , ,以BC的中点O为圆心的 分别与AB,AC相切于D,E两点,则 的长为( )
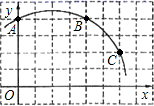
A、( )° B、( )° C、( )° D、( )°8. 一段圆弧的半径是12,弧长是 ,则这段圆弧所对的圆心角是( )A、 B、 C、 D、9. 如图,在 中, , ,以BC的中点O为圆心的 分别与AB,AC相切于D,E两点,则 的长为( )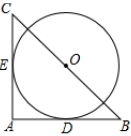 A、 B、 C、 D、10. 如图,5×3的网格图中,每个小正方形的边长均为1,设经过图中格点A,C,B三点的圆弧与AE交于H,则弧AH的弧长为( )
A、 B、 C、 D、10. 如图,5×3的网格图中,每个小正方形的边长均为1,设经过图中格点A,C,B三点的圆弧与AE交于H,则弧AH的弧长为( )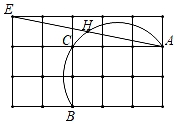 A、 π B、 π C、 π D、 π
A、 π B、 π C、 π D、 π二、填空题
-
11. 一个扇形的弧长是 ,它的面积为 ,则这个扇形的圆心角度数为度.12. 若一个扇形的圆心角为 ,面积为 ,则这个扇形的弧长为 (结果保留 )13. 如图,用一个圆心角为120°的扇形围成一个无底的圆锥,如果这个圆锥底面圆的半径为 ,则这个扇形的半径是 .
 14. 如图,在平行四边形ABCD中,AD=4,∠C=30°,⊙O与AD相交于点F,AB为⊙O的直径,⊙O与CD的延长线相切于点E,则劣弧FE的长为
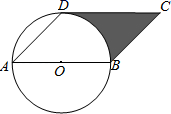
14. 如图,在平行四边形ABCD中,AD=4,∠C=30°,⊙O与AD相交于点F,AB为⊙O的直径,⊙O与CD的延长线相切于点E,则劣弧FE的长为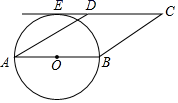 15. 如图, 为 的直径, ,点 为圆上一点,将劣弧 沿弦 翻折交 于点 ,则劣弧 的弧长是 .
15. 如图, 为 的直径, ,点 为圆上一点,将劣弧 沿弦 翻折交 于点 ,则劣弧 的弧长是 .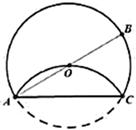
三、解答题
-
16. 如图,已知AB是O的直径,点C,D在⊙O上,点E在O外,∠EAC=∠D=60∘,BC=6.求劣弧AC的长.
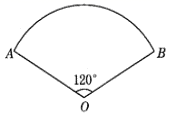
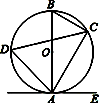 17. 如图,阴影部分是一广告标志,已知两圆弧所在圆的半径分别是20cm,10cm,∠AOB=120°,则这个广告标志的周长是多少?
17. 如图,阴影部分是一广告标志,已知两圆弧所在圆的半径分别是20cm,10cm,∠AOB=120°,则这个广告标志的周长是多少?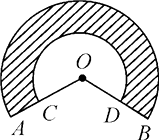 18. 如图,在△ABC中,以AB为直径的⊙O分别于BC,AC相交于点D,E,BD=CD,过点D作⊙O的切线交边AC于点F.
18. 如图,在△ABC中,以AB为直径的⊙O分别于BC,AC相交于点D,E,BD=CD,过点D作⊙O的切线交边AC于点F.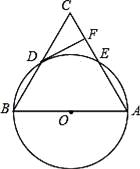 (1)、求证:DF⊥AC;(2)、若⊙O的半径为5,∠CDF=30°,求 的长(结果保留π).19. 如图,AB为⊙O的直径,点C在⊙O外,∠ABC的平分线与⊙O交于点D,∠C=90°.
(1)、求证:DF⊥AC;(2)、若⊙O的半径为5,∠CDF=30°,求 的长(结果保留π).19. 如图,AB为⊙O的直径,点C在⊙O外,∠ABC的平分线与⊙O交于点D,∠C=90°.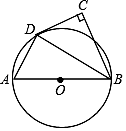 (1)、CD与⊙O有怎样的位置关系?请说明理由;(2)、若∠CDB=60°,AB=6,求 的长.20. 如图,已知△ABC是⊙O的内接三角形,AD是⊙O的直径,连结BD,BC平分∠ABD.
(1)、CD与⊙O有怎样的位置关系?请说明理由;(2)、若∠CDB=60°,AB=6,求 的长.20. 如图,已知△ABC是⊙O的内接三角形,AD是⊙O的直径,连结BD,BC平分∠ABD.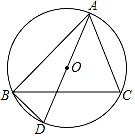 (1)、求证:∠CAD=∠ABC;(2)、若AD=6,求 的长.21. 如图,四边形ABCD是⊙O的内接四边形,四边形ABCD两组对边的延长线分别相交于点E,F,且∠E=40°,∠F=50°,连接BD.
(1)、求证:∠CAD=∠ABC;(2)、若AD=6,求 的长.21. 如图,四边形ABCD是⊙O的内接四边形,四边形ABCD两组对边的延长线分别相交于点E,F,且∠E=40°,∠F=50°,连接BD.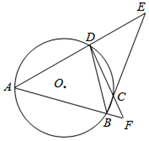 (1)、求∠A的度数;(2)、当⊙O的半径等于2时,请直接写出弧BD的长(结果保留π)22. 如图,AB为⊙O的直径,C,D为⊙O上的两点,∠BAC=∠DAC,过点C做直线EF⊥AD,交AD的延长线于点E,连接BC.
(1)、求∠A的度数;(2)、当⊙O的半径等于2时,请直接写出弧BD的长(结果保留π)22. 如图,AB为⊙O的直径,C,D为⊙O上的两点,∠BAC=∠DAC,过点C做直线EF⊥AD,交AD的延长线于点E,连接BC.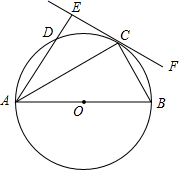 (1)、求证:EF是⊙O的切线.(2)、若∠CAO=30°,BC=2,求劣弧BC的长.23. 如图,在△ABC中,E是内心,AE的延长线和△ABC的外接圆相交于点D.
(1)、求证:EF是⊙O的切线.(2)、若∠CAO=30°,BC=2,求劣弧BC的长.23. 如图,在△ABC中,E是内心,AE的延长线和△ABC的外接圆相交于点D. (1)、求证:DB=DC;(2)、若AB=AC,∠BAC=80°,AD=3.求 的长.
(1)、求证:DB=DC;(2)、若AB=AC,∠BAC=80°,AD=3.求 的长.