初中数学苏科版九年级上学期期中复习专题8 正多边形与圆
试卷更新日期:2020-10-27 类型:复习试卷
一、单选题
-
1. 如图,正六边形ABCDEF内接于⊙O,点P是 上的任意一点,则∠APB的大小是( )
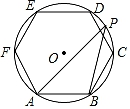 A、15° B、30° C、45° D、60°2. 如图,将边长为3的正六边形铁丝框ABCDEF(面积记为S1)变形为以点D为圆心,CD为半径的扇形(面积记为S2),则S1与S2的关系为( )
A、15° B、30° C、45° D、60°2. 如图,将边长为3的正六边形铁丝框ABCDEF(面积记为S1)变形为以点D为圆心,CD为半径的扇形(面积记为S2),则S1与S2的关系为( )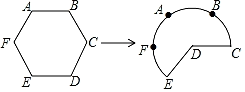 A、S1>S2 B、S1=S2 C、S1<S2 D、S1= S23. 如图中有两张型号完全一样的折叠式饭桌,将正方形桌面边上的四个弓形翻折起来后,就能形成一个圆形桌面(可以近似看作正方形的外接圆),正方形桌面与翻折成圆形桌面的面积之比最接近( )
A、S1>S2 B、S1=S2 C、S1<S2 D、S1= S23. 如图中有两张型号完全一样的折叠式饭桌,将正方形桌面边上的四个弓形翻折起来后,就能形成一个圆形桌面(可以近似看作正方形的外接圆),正方形桌面与翻折成圆形桌面的面积之比最接近( )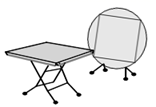 A、 B、 C、 D、4. 如图, 与正六边形 的边 分别交于点 ,点M为劣弧 的中点.若 .则点O到 的距离是( )
A、 B、 C、 D、4. 如图, 与正六边形 的边 分别交于点 ,点M为劣弧 的中点.若 .则点O到 的距离是( )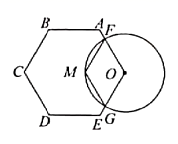 A、4 B、 C、 D、5. 如图,正方形ABCD和等边△AEF都内接于圆O,EF与BC,CD别相交于点G,H.若AE=6,则EG的长为( )
A、4 B、 C、 D、5. 如图,正方形ABCD和等边△AEF都内接于圆O,EF与BC,CD别相交于点G,H.若AE=6,则EG的长为( )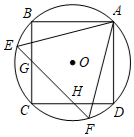 A、 B、3﹣ C、 D、2 ﹣36. 如图,若干全等正五边形排成环状.图中所示的是前3个正五边形,则要完成这一圆环还需( )个这样的正五边形
A、 B、3﹣ C、 D、2 ﹣36. 如图,若干全等正五边形排成环状.图中所示的是前3个正五边形,则要完成这一圆环还需( )个这样的正五边形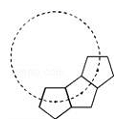 A、6 B、7 C、8 D、97. 如图,⊙O的周长等于4πcm,则它的内接正六边形ABCDEF的面积是( )
A、6 B、7 C、8 D、97. 如图,⊙O的周长等于4πcm,则它的内接正六边形ABCDEF的面积是( ) A、 B、 C、 D、8. 如图,正五边形ABCDE和正三角形AMN都是⊙O的内接多边形,若连接BM,则的度数是( )
A、 B、 C、 D、8. 如图,正五边形ABCDE和正三角形AMN都是⊙O的内接多边形,若连接BM,则的度数是( )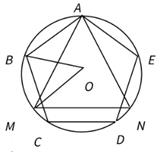 A、12° B、15° C、30° D、48°9. 如图,正五边形ABCDE的边长为2,连结AC、AD、BE,BE分别与AC和AD相交于点F、G,连结DF,给出下列结论:①∠FDG=18°;②FG=3﹣ ;③(S四边形CDEF)2=9+2 ;④DF2﹣DG2=7﹣2 .其中结论正确的个数是( )
A、12° B、15° C、30° D、48°9. 如图,正五边形ABCDE的边长为2,连结AC、AD、BE,BE分别与AC和AD相交于点F、G,连结DF,给出下列结论:①∠FDG=18°;②FG=3﹣ ;③(S四边形CDEF)2=9+2 ;④DF2﹣DG2=7﹣2 .其中结论正确的个数是( )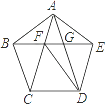 A、1 B、2 C、3 D、410. 如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是( )
A、1 B、2 C、3 D、410. 如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是( )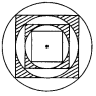 A、()nR B、()nR C、()n-1R D、()n-1R
A、()nR B、()nR C、()n-1R D、()n-1R二、填空题
-
11. 如图,边长为2 cm的正六边形螺帽,中心为点O,OA垂直平分边CD,垂足为B,AB=17cm,用扳手拧动螺帽旋转90°,则点A在该过程中所经过的路径长为cm.
 12. 如图,已知正六边形 ,连接 ,则 °.
12. 如图,已知正六边形 ,连接 ,则 °.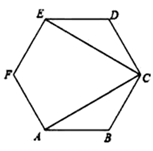 13. 如图,在正十边形A1A2A3A4A5A6A7A8A9A10中,连接A1A4、A1A7 , 则∠A4A1A7=°.
13. 如图,在正十边形A1A2A3A4A5A6A7A8A9A10中,连接A1A4、A1A7 , 则∠A4A1A7=°.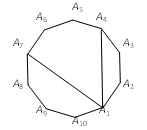 14. 如图,以正六边形ABCDEF的中心为坐标原点建立平面直角坐标系,顶点C、F在x轴上,顶点A的坐标为(1, ),则顶点D的坐标为 .
14. 如图,以正六边形ABCDEF的中心为坐标原点建立平面直角坐标系,顶点C、F在x轴上,顶点A的坐标为(1, ),则顶点D的坐标为 .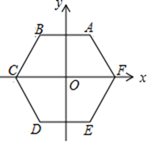 15. 如图,⊙O的半径为r,则它的内接正六边形ABCDEF的周长为.
15. 如图,⊙O的半径为r,则它的内接正六边形ABCDEF的周长为.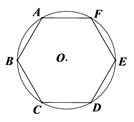 16. 如图,点M、N分别是正五边形ABCDE的两边AB、BC上的点.且AM=BN,点O是正五边形的中心,则∠MON的度数是度.
16. 如图,点M、N分别是正五边形ABCDE的两边AB、BC上的点.且AM=BN,点O是正五边形的中心,则∠MON的度数是度.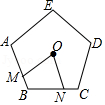 17. 如图,△PQR是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形,BC∥QR,则∠AOQ=。
17. 如图,△PQR是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形,BC∥QR,则∠AOQ=。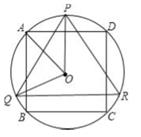 18. 如图,正六边形ABCDEF内接于⊙O , AB=2,则图中阴影部分的面积为
18. 如图,正六边形ABCDEF内接于⊙O , AB=2,则图中阴影部分的面积为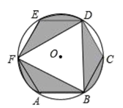
三、解答题
-
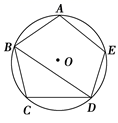
19. 如图, 是 的内接正五边形.求证: .
 20. 如图,已知正三角形ABC内接于 ,AD是 的内接正十二边形的一条边长,连接CD,若 ,求 的半径.
20. 如图,已知正三角形ABC内接于 ,AD是 的内接正十二边形的一条边长,连接CD,若 ,求 的半径.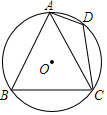 21. 如图,正方形ABCD的外接圆为⊙O,点P在劣弧 上(不与C点重合).
21. 如图,正方形ABCD的外接圆为⊙O,点P在劣弧 上(不与C点重合).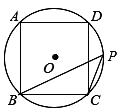 (1)、求∠BPC的度数;
(1)、求∠BPC的度数;
(2)、若⊙O的半径为8,求正方形ABCD的边长.22. 如图,在平面直角坐标系中,正六边形ABCDEF的对称中心P在反比例函数 的图象上,边CD在x轴上,点B在y轴上.已知 .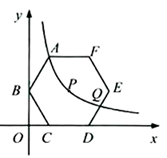 (1)、点A是否在该反比例函数的图象上?请说明理由.(2)、若该反比例函数图象与DE交于点Q,求点Q的横坐标.(3)、平移正六边形ABCDEF,使其一边的两个端点恰好都落在该反比例函数的图象上,试描述平移过程.23. 如图(1),正五边形ABCDE与⊙O相切于点A,点C在⊙O上.
(1)、点A是否在该反比例函数的图象上?请说明理由.(2)、若该反比例函数图象与DE交于点Q,求点Q的横坐标.(3)、平移正六边形ABCDEF,使其一边的两个端点恰好都落在该反比例函数的图象上,试描述平移过程.23. 如图(1),正五边形ABCDE与⊙O相切于点A,点C在⊙O上.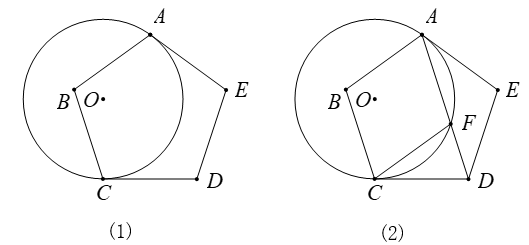 (1)、求证:CD是⊙O的切线;(2)、若⊙O的半径为5,求劣弧AC的长度;(3)、如图(2),连接AD交⊙O于点F.求证:四边形ABCF是菱形.24. 如图,正五边形ABCD中,点F、G分别是BC、CD的中点,AF与BG相交于H.
(1)、求证:CD是⊙O的切线;(2)、若⊙O的半径为5,求劣弧AC的长度;(3)、如图(2),连接AD交⊙O于点F.求证:四边形ABCF是菱形.24. 如图,正五边形ABCD中,点F、G分别是BC、CD的中点,AF与BG相交于H.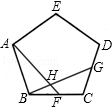 (1)、求证:△ABF≌△BCG;(2)、求∠AHG的度数.25. 如图
(1)、求证:△ABF≌△BCG;(2)、求∠AHG的度数.25. 如图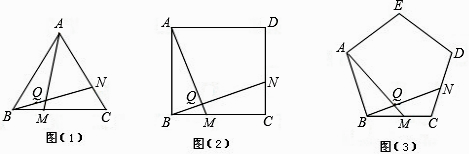 (1)、如图(1),已知△ABC为正三角形,点M是BC上一点,点N是AC上一点,AM、BN相交于点Q,BM=CN.求出∠BQM的度数;(2)、将(1)中的“正△ABC”分别改为正方形ABCD、正五边形ABCDE、…正n边形ABCD…,“点N是AC上一点”改为点N是CD上一点,其余条件不变,分别推断出∠BQM等于多少度,将结论填入下表:
(1)、如图(1),已知△ABC为正三角形,点M是BC上一点,点N是AC上一点,AM、BN相交于点Q,BM=CN.求出∠BQM的度数;(2)、将(1)中的“正△ABC”分别改为正方形ABCD、正五边形ABCDE、…正n边形ABCD…,“点N是AC上一点”改为点N是CD上一点,其余条件不变,分别推断出∠BQM等于多少度,将结论填入下表:正多边形
正方形
正五边形
……
正n边形
∠BQM的度数
……
26. 如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=120°,点E在上.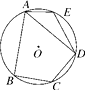 (1)、求∠AED的度数;
(1)、求∠AED的度数;
(2)、若⊙O的半径为2,则弧AD的长为多少?
(3)、连接OD,OE,当∠DOE=90°时,AE恰好是⊙O内接正n边形的一边,求n的值.27. 如图①、②、③,正三角形ABC、正方形ABCD、正五边形ABCDE分别是⊙O的内接三角形、内接四边形、内接五边形,点M、N分别从点B,C开始,以相同的速度中⊙O上逆时针运动.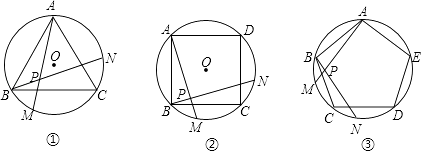 (1)、求图①中∠APB的度数;
(1)、求图①中∠APB的度数;
(2)、图②中,∠APB的度数是 , 图③中∠APB的度数是;(3)、根据前面探索,你能否将本题推广到一般的正n边形情况?若能,写出推广问题和结论;若不能,请说明理由.