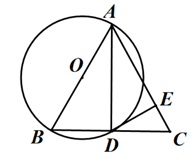初中数学苏科版九年级上学期期中复习专题7 直线与圆的位置关系
试卷更新日期:2020-10-27 类型:复习试卷
一、单选题
-
1. 如图,在⊙O中,AB为弦,OD⊥AB于D,∠BOD=53°,过A作⊙O的切线交OD延长线于C,则∠C=( )
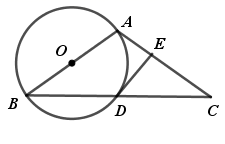
 A、27° B、30° C、37° D、53°2. 如图, 是 的弦,点 在过点 的切线上, , 交 于点 .若 ,则 的度数等于( )
A、27° B、30° C、37° D、53°2. 如图, 是 的弦,点 在过点 的切线上, , 交 于点 .若 ,则 的度数等于( )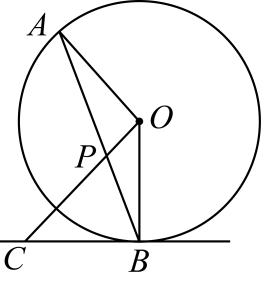 A、 B、 C、 D、3. 如图, 内接于圆, ,过点C的切线交 的延长线于点 .则 ( )
A、 B、 C、 D、3. 如图, 内接于圆, ,过点C的切线交 的延长线于点 .则 ( )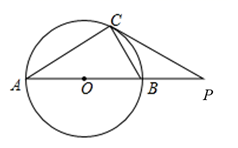 A、 B、 C、 D、4. 下列命题是真命题的是( )A、顶点在圆上的角叫圆周角 B、三点确定一个圆 C、圆的切线垂直于半径 D、三角形的内心到三角形三边的距离相等5. 如图,已知 是 的两条切线,A , B为切点,线段 交 于点M . 给出下列四种说法:① ;② ;③四边形 有外接圆;④M是 外接圆的圆心,其中正确说法的个数是( )
A、 B、 C、 D、4. 下列命题是真命题的是( )A、顶点在圆上的角叫圆周角 B、三点确定一个圆 C、圆的切线垂直于半径 D、三角形的内心到三角形三边的距离相等5. 如图,已知 是 的两条切线,A , B为切点,线段 交 于点M . 给出下列四种说法:① ;② ;③四边形 有外接圆;④M是 外接圆的圆心,其中正确说法的个数是( )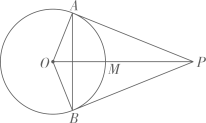 A、1 B、2 C、3 D、46. 如图,在平面直角坐标系中,点 在第一象限,⊙P与x轴、y轴都相切,且经过矩形 的顶点C,与BC相交于点D,若⊙P的半径为5,点 的坐标是 ,则点D的坐标是( )
A、1 B、2 C、3 D、46. 如图,在平面直角坐标系中,点 在第一象限,⊙P与x轴、y轴都相切,且经过矩形 的顶点C,与BC相交于点D,若⊙P的半径为5,点 的坐标是 ,则点D的坐标是( )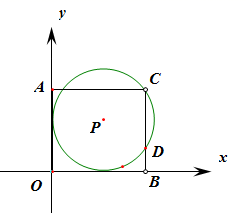 A、 B、 C、 D、7. 设边长为a的等边三角形的高、内切圆的半径、外接圆的半径分别为h、r、R,则下列结论不正确的是( )
A、 B、 C、 D、7. 设边长为a的等边三角形的高、内切圆的半径、外接圆的半径分别为h、r、R,则下列结论不正确的是( )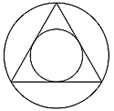 A、 B、 C、 D、8. 如图所示, 、 分别与 相切于A、B两点,点C为 上一点,连接 、 ,若 ,则 的度数为( )
A、 B、 C、 D、8. 如图所示, 、 分别与 相切于A、B两点,点C为 上一点,连接 、 ,若 ,则 的度数为( )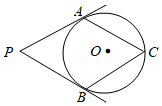 A、 B、 C、 D、9. 如图,在矩形 中, , , ,则 内切圆的半径是( )
A、 B、 C、 D、9. 如图,在矩形 中, , , ,则 内切圆的半径是( )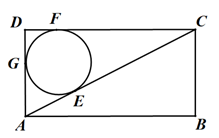 A、1 B、2 C、3 D、410. 如图,AB是⊙O的直径,点P在BA的延长线上,PA=AO,PD与⊙O相切于点D,BC⊥AB交PD的延长线于点C,若⊙O的半径为1,则BC的长是( )
A、1 B、2 C、3 D、410. 如图,AB是⊙O的直径,点P在BA的延长线上,PA=AO,PD与⊙O相切于点D,BC⊥AB交PD的延长线于点C,若⊙O的半径为1,则BC的长是( )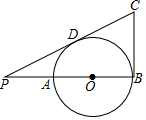 A、1.5 B、2 C、 D、
A、1.5 B、2 C、 D、二、填空题
-
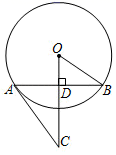
11. 如图,已知 是 的直径, 是 的切线,连接 交 于点D,连接 .若 ,则 的度数是 .
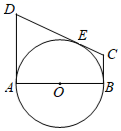
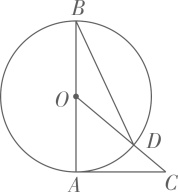 12. 如图,PA切⊙O于点A , PC过点O且与⊙O交于B , C两点,若PA=6cm , PB=2 cm , 则△PAC的面积是cm2 .
12. 如图,PA切⊙O于点A , PC过点O且与⊙O交于B , C两点,若PA=6cm , PB=2 cm , 则△PAC的面积是cm2 .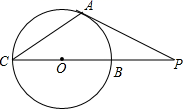 13. 如图,在Rt△ABC中,∠C=90°,过点C作△ABC外接圆⊙O的切线交AB的垂直平分线于点D,AB的垂直平分线交AC于点E,若OE=2,AB=8,则CD=。
13. 如图,在Rt△ABC中,∠C=90°,过点C作△ABC外接圆⊙O的切线交AB的垂直平分线于点D,AB的垂直平分线交AC于点E,若OE=2,AB=8,则CD=。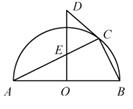 14. 如图, 为 的直径, 与 相切于点 ,弦 .若 ,则 .
14. 如图, 为 的直径, 与 相切于点 ,弦 .若 ,则 .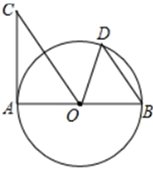 15. 如图,以△ABC的边AB为直径的⊙O恰好过BC的中点D,过点D作DE⊥AC于E,连结OD,则下列结论中:①OD∥AC;②∠B=∠C;③2OA=BC;④DE是⊙O的切线;⑤∠EDA=∠B,正确的序号是.
15. 如图,以△ABC的边AB为直径的⊙O恰好过BC的中点D,过点D作DE⊥AC于E,连结OD,则下列结论中:①OD∥AC;②∠B=∠C;③2OA=BC;④DE是⊙O的切线;⑤∠EDA=∠B,正确的序号是.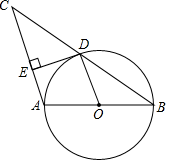 16. 如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=4,⊙O的半径为2,点P是AB边上的动点,过点P作⊙O的一条切线PC(点C为切点),则线段PC长的最小值为.
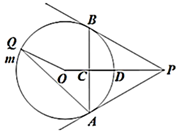
16. 如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=4,⊙O的半径为2,点P是AB边上的动点,过点P作⊙O的一条切线PC(点C为切点),则线段PC长的最小值为.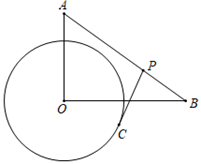 17. 如图,PA、PB切00于A、B两点,连接OP交AB于点C,交弧AB于点D, ,点Q为优弧AmB上一点, , 则∠OQA的大小为.
17. 如图,PA、PB切00于A、B两点,连接OP交AB于点C,交弧AB于点D, ,点Q为优弧AmB上一点, , 则∠OQA的大小为.
 18. 图1是一种推磨工具模型,图2是它的示意图,已知AB⊥PQ,AP=AQ=3dm,AB=12dm,点A在中轴线l上运动,点B在以O为圆心,OB长为半径的圆上运动,且OB=4dm.
18. 图1是一种推磨工具模型,图2是它的示意图,已知AB⊥PQ,AP=AQ=3dm,AB=12dm,点A在中轴线l上运动,点B在以O为圆心,OB长为半径的圆上运动,且OB=4dm.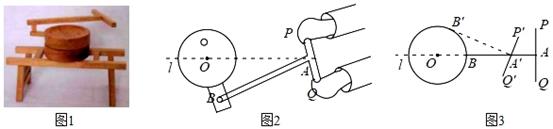 (1)、如图3,当点B按逆时针方向运动到B′时,A′B′与⊙O相切,则AA′= dm.(2)、在点B的运动过程中,点P与点O之间的最短距离为 dm.
(1)、如图3,当点B按逆时针方向运动到B′时,A′B′与⊙O相切,则AA′= dm.(2)、在点B的运动过程中,点P与点O之间的最短距离为 dm.三、综合题
-
19. 如图, 是 的外接圆, 是 的直径, .
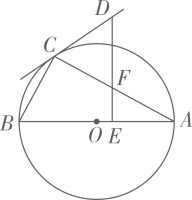 (1)、求证: 是 的切线;(2)、若 ,垂足为 交 与点;求证: 是等腰三角形.20. 如图, 是 的直径,点D在 上, 的延长线与过点B的切线交于点C , E为线段 上的点,过点E的弦 于点H .
(1)、求证: 是 的切线;(2)、若 ,垂足为 交 与点;求证: 是等腰三角形.20. 如图, 是 的直径,点D在 上, 的延长线与过点B的切线交于点C , E为线段 上的点,过点E的弦 于点H .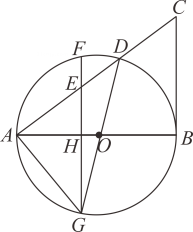 (1)、求证: ;(2)、已知 , ,且 ,求 的长.
(1)、求证: ;(2)、已知 , ,且 ,求 的长.