初中数学苏科版八年级上册6.6 一次函数、一元一次方程和一元一次不等式
试卷更新日期:2020-10-27 类型:同步测试
一、单选题
-
1. 如图,直线y=kx+b(k≠0)经过点(-1,3),则不等式kx+b≥3解集为( )
 A、x≤-1 B、x≥-1 C、x≤3 D、x≥32. 如图,直线 与 相交于点P,若点P的横坐标为-1,则关于x的不等式 的解集是( )
A、x≤-1 B、x≥-1 C、x≤3 D、x≥32. 如图,直线 与 相交于点P,若点P的横坐标为-1,则关于x的不等式 的解集是( )
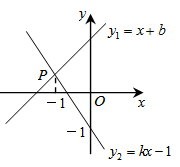 A、 B、 C、 D、3. 如图,一次函数 的图象经过点 ,则关于 的不等式 的解集为( )
A、 B、 C、 D、3. 如图,一次函数 的图象经过点 ,则关于 的不等式 的解集为( )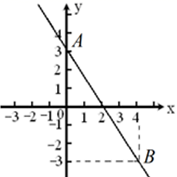 A、 B、 C、 D、4. 如图,直线 经过点 和点 ,直线 过点 则不等式 的解集为( )
A、 B、 C、 D、4. 如图,直线 经过点 和点 ,直线 过点 则不等式 的解集为( )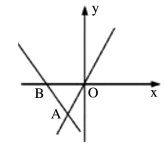 A、 B、 C、 D、5. 如图,直线y=kx和y=ax+4交于A(1,k),则不等式kx﹣6<ax+4<kx的解集为( )
A、 B、 C、 D、5. 如图,直线y=kx和y=ax+4交于A(1,k),则不等式kx﹣6<ax+4<kx的解集为( )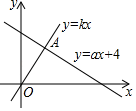 A、1<x< B、1<x<3 C、﹣ <x<1 D、 <x<36. 已知一次函数y=kx+b(k、b是常数,且k≠0),x与y的部分对应值如表所示,那么不等式kx+b<0的解集是( )
A、1<x< B、1<x<3 C、﹣ <x<1 D、 <x<36. 已知一次函数y=kx+b(k、b是常数,且k≠0),x与y的部分对应值如表所示,那么不等式kx+b<0的解集是( )x
﹣2
﹣1
0
1
2
3
y
3
2
1
0
﹣1
﹣2
A、x<0 B、x>0 C、x>1 D、x<27. 如图所示,函数y1=|x|和 的图象相交于(﹣1,1),(2,2)两点.当y1>y2时,x的取值范围是( ) A、x<﹣1 B、﹣1<x<2 C、x>2 D、x<﹣1或x>28. 如图,已知直线 和直线 交于点 ,则关于x的不等式 的解是( )
A、x<﹣1 B、﹣1<x<2 C、x>2 D、x<﹣1或x>28. 如图,已知直线 和直线 交于点 ,则关于x的不等式 的解是( )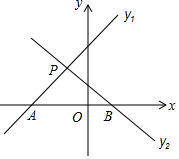 A、 B、 C、 D、9. 如图,直线y=kx+b与y=mx+n分别交x轴于点A(﹣0.5,0)、B(2,0),则不等式(kx+b)(mx+n)<0的解集为( )
A、 B、 C、 D、9. 如图,直线y=kx+b与y=mx+n分别交x轴于点A(﹣0.5,0)、B(2,0),则不等式(kx+b)(mx+n)<0的解集为( )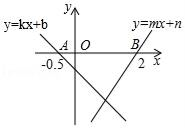 A、x>2 B、﹣0.5<x<2 C、0<x<2 D、x<﹣0.5或x>210.
A、x>2 B、﹣0.5<x<2 C、0<x<2 D、x<﹣0.5或x>210.如图所示,两函数y1=k1x+b和y2=k2x的图象相交于点(-1,-2),则关于x的不等式 k1x+b>k2x的解集为( )
 A、x>-1 B、x<-1 C、x<-2 D、无法确定
A、x>-1 B、x<-1 C、x<-2 D、无法确定二、填空题
-
11. 函数y=kx与y=6﹣x的图象如图所示,则不等式6﹣x≥kx的解集为 .
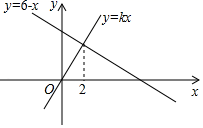 12. 一次函数
12. 一次函数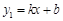 与
与  的图象如图,则
的图象如图,则 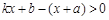 的解集是 .
的解集是 . 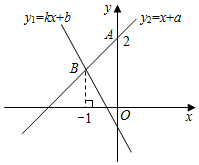 13. 如图,函数y=kx和y=ax+b的图象交于点P,根据图象可得不等式 >0的解集是
13. 如图,函数y=kx和y=ax+b的图象交于点P,根据图象可得不等式 >0的解集是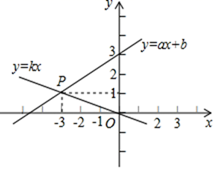 14. 如图,直线y=-x+m与y=nx+4n的交点的横坐标为-2,则关于x的不等式-x+m>nx+4n>0的解集为.
14. 如图,直线y=-x+m与y=nx+4n的交点的横坐标为-2,则关于x的不等式-x+m>nx+4n>0的解集为.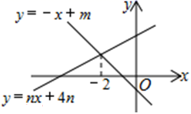 15. 如图,关于x的一次函数l1:y1=k1x+b1 , l2:y2=k2x+b2的图象交于点(1,3),则关于x的不等式 的解集为 .
15. 如图,关于x的一次函数l1:y1=k1x+b1 , l2:y2=k2x+b2的图象交于点(1,3),则关于x的不等式 的解集为 .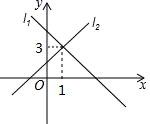 16. 如图,在坐标系中,一次函数 与一次函数 的图像交于点 ,则关于 的不等式 的解集是.
16. 如图,在坐标系中,一次函数 与一次函数 的图像交于点 ,则关于 的不等式 的解集是.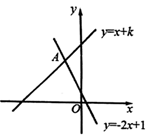 17. 如图,一次函数y=﹣x﹣2与y=2x+m的图象相交于点P(n,﹣4),则关于x的不等式2x+m<﹣x﹣2<0的解集为.
17. 如图,一次函数y=﹣x﹣2与y=2x+m的图象相交于点P(n,﹣4),则关于x的不等式2x+m<﹣x﹣2<0的解集为.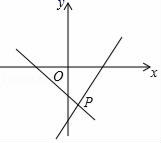 18. 如图,一次函数 与 的图象相交于点 ,则关于x的不等式 的解集是.
18. 如图,一次函数 与 的图象相交于点 ,则关于x的不等式 的解集是.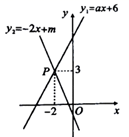 19. 已知一次函数 为常数),当x<2时,y>0,则 的取值范围为 .20. 如图,在平面直角坐标系 中,直线 , 分别是函数 和 的图象,则关于 的不等式 的解集为 .若 , 分别满足方程 和 ,则 , 的大小关系是 .(填或“ ”“ ”“ ”)
19. 已知一次函数 为常数),当x<2时,y>0,则 的取值范围为 .20. 如图,在平面直角坐标系 中,直线 , 分别是函数 和 的图象,则关于 的不等式 的解集为 .若 , 分别满足方程 和 ,则 , 的大小关系是 .(填或“ ”“ ”“ ”)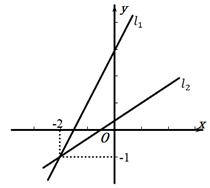
三、解答题
-
21. 如图,函数y=2x和y=ax+4的图象相交于点A(m,3)
(1)求m,a的值;
(2)根据图象,直接写出不等式2x>ax+4的解集.
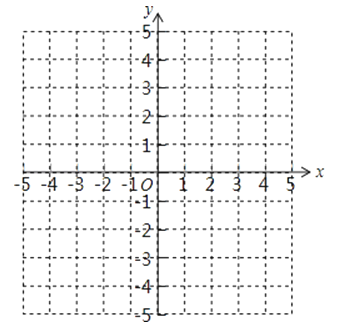
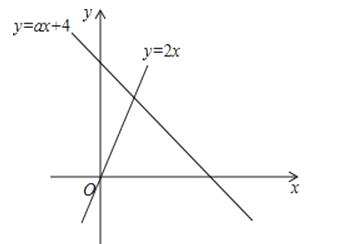 22. 已知一次函数y1=﹣2x﹣3与y2=x+2.
22. 已知一次函数y1=﹣2x﹣3与y2=x+2.(1)在同一平面直角坐标系中,画出这两个函数的图象;
(2)根据图象,不等式﹣2x﹣3>x+2的解集为多少?
(3)求两图象和y轴围成的三角形的面积.
 23. 为倡导绿色出行,某共享单车近期登陆徐州,根据连续骑行时长分段计费:骑行时长在2h以内(含2h)的部分,每0.5h计费1元(不足0.5h按0.5h计算); 骑行时长超出2h的部分,每小时计费4元(不足1h按1h计算).
23. 为倡导绿色出行,某共享单车近期登陆徐州,根据连续骑行时长分段计费:骑行时长在2h以内(含2h)的部分,每0.5h计费1元(不足0.5h按0.5h计算); 骑行时长超出2h的部分,每小时计费4元(不足1h按1h计算).根据此收费标准,解决下列问题:
(1)、连续骑行5h,应付费多少元?(2)、若连续骑行xh(x>2且x为整数) 需付费y元,则y与x的函数表达式为;(3)、若某人连续骑行后付费24元,求其连续骑行时长的范围.24. 如图,直线l1:y1=﹣ x+m与y轴交于点A(0,6),直线l2:y2=kx+1分别与x轴交于点B(﹣2,0),与y轴交于点C.两条直线相交于点D,连接AB.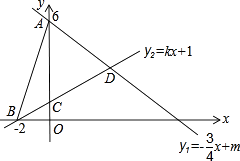 (1)、求两直线交点D的坐标;(2)、求△ABD的面积;(3)、根据图象直接写出y1>y2时自变量x的取值范围.25. 某学校为了改善办学条件,计划购置一批电子白板和一批笔记本电脑,经投标,购买1块电子白板比买3台笔记本电脑多3000元,购买4块电子白板和5台笔记本电脑共需80000元.(1)、求购买1块电子白板和一台笔记本电脑各需多少元?(2)、根据该校实际情况,需购买电子白板和笔记本电脑的总数为396,要求购买的总费用不超过2700000元,并购买笔记本电脑的台数不超过购买电子白板数量的3倍,该校有哪几种购买方案?(3)、上面的哪种购买方案最省钱?按最省钱方案购买需要多少钱?26. 已知一次函数 ,其中 .(1)、若点 在y1的图象上.求a的值:(2)、当 时.若函数有最大值2.求y1的函数表达式;(3)、对于一次函数 ,其中 ,若对一切实数x, 都成立,求a,m需满足的数量关系及 a的取值范围.
(1)、求两直线交点D的坐标;(2)、求△ABD的面积;(3)、根据图象直接写出y1>y2时自变量x的取值范围.25. 某学校为了改善办学条件,计划购置一批电子白板和一批笔记本电脑,经投标,购买1块电子白板比买3台笔记本电脑多3000元,购买4块电子白板和5台笔记本电脑共需80000元.(1)、求购买1块电子白板和一台笔记本电脑各需多少元?(2)、根据该校实际情况,需购买电子白板和笔记本电脑的总数为396,要求购买的总费用不超过2700000元,并购买笔记本电脑的台数不超过购买电子白板数量的3倍,该校有哪几种购买方案?(3)、上面的哪种购买方案最省钱?按最省钱方案购买需要多少钱?26. 已知一次函数 ,其中 .(1)、若点 在y1的图象上.求a的值:(2)、当 时.若函数有最大值2.求y1的函数表达式;(3)、对于一次函数 ,其中 ,若对一切实数x, 都成立,求a,m需满足的数量关系及 a的取值范围.