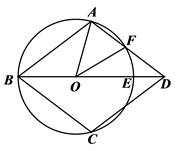初中数学苏科版九年级上学期期中复习专题6 圆周角定理
试卷更新日期：2020-10-27 类型：复习试卷
一、单选题
-
1. 如图，点A，B，C，D在⊙O上， ，点B是弧AC的中点，则 的度数是（ ）
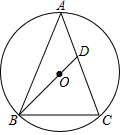
A、30° B、40° C、50° D、60°2.如图，AB和CD都是⊙O的直径，∠AOC=52°，则∠C的度数是（ ）
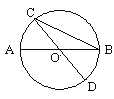A、22° B、26° C、38° D、48°3. 如图，AB为⊙O的直径，C，D为⊙O上两点，若∠BCD＝40°，则∠ABD的大小为（ ）
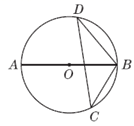A、60° B、50° C、40° D、30°4. 如图， 为⊙ 的直径，C，D是圆周上的两点，若 ，则锐角 的度数为（ ）
A、57° B、52° C、38° D、26°5. 如图，AB是⊙O的直径，弦CD⊥AB，垂足为M，下列结论不成立的是（ ）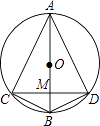
A、CM=DM B、 C、∠ACD=∠ADC D、OM=BM6. 如图， 中， ，则 的度数为（ ）
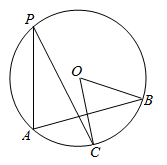A、 B、 C、 D、7. 如图，已知BC是⊙O的直径，半径OA⊥BC，点D在劣弧AC上(不与点A，点C重合)，BD与OA交于点E，设∠AED=α，∠AOD=β，则（ ）
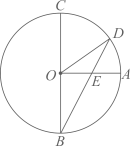A、3α+β=180° B、2α+β=180° C、3α-β=90° D、2α-β=90°8. 数学课上，老师让学生尺规作图画Rt△ABC，使其斜边AB=c，一条直角边BC=a．小明的作法如图所示，你认为这种作法中判断∠ACB是直角的依据是（ ）
A、勾股定理 B、直径所对的圆周角是直角 C、勾股定理的逆定理 D、90°的圆周角所对的弦是直径9. 如图，在⊙O中，若∠CDB＝60°，⊙O的直径AB等于4，则BC的长为（ ）
A、 B、2 C、2 D、410. 如图，在 中， 的度数为 是 上一点， 是 上不同的两点（不与 两点重合）， 的度数为（ ）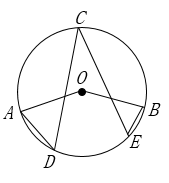
A、m B、 C、 D、二、填空题
-
11. 如图，AB是 的直径，点C，D，E都在 上，∠1=55°，则∠2=°
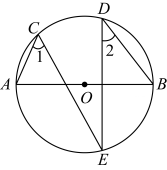12. 如图，AB是半圆O的直径，AC＝AD，OC＝2，∠CAB＝30°，则点O到CD的距离OE为.
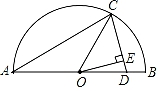13. 如图，⊙O中，直径CD⊥弦AB于E，AM⊥BC于M，交CD于N，连AD.AB= ，ON=1，则⊙O的半径长为.
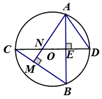14. 如图，四边形ABCD是菱形，⊙O经过点A、C、D，与BC相交于点E，连接AC、AE.若∠D＝70°，则∠EAC的度数为.
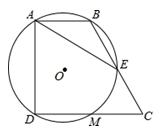
15. 如图，半径为5的⊙A中，弦BC，ED所对的圆心角分别是∠BAC，∠EAD.已知DE=6，∠BAC+∠EAD=180°，则弦BC的弦心距等于.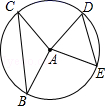
16. 如图，在四边形ABCD中，∠BAD=∠CDA=90°，AB=1，CD=2，过A，B，D三点的⊙O分别交BC，CD于点E，M，下列结论：①DM=CM；②弧AB=弧EM；③⊙O的直径为2；④AE=AD.
其中正确的结论有（填序号）.
三、综合题
-
17. 如图，在⊙O中，弧AC=BC，CD⊥OA于D，CE⊥OB于E.求证：AD＝BE.
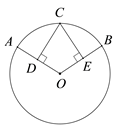18. 如图，△ABC的三个顶点都在⊙O上，直径AD＝6cm ， ∠DAC＝2∠B ， 求AC的长．
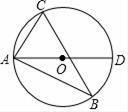19. 如图， 、 是 的两条弦，且 ，点 是弧BC的中点，连接并延长 、 ，分别交 、 的延长线于点 、 .
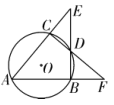(1)、求证： ；(2)、若 ， ，求 的半径.
