初中数学苏科版九年级上学期期中复习专题5 圆的认识
试卷更新日期：2020-10-27 类型：复习试卷
一、单选题
-
1. 下列语句中正确的是（ ）A、直径是弦，弦是直径． B、相等的圆心角所对的弦相等 C、经过圆心的每一条直线都是圆的对称轴 D、三点确定一个圆2. 一个点到圆的最大距离为11，最小距离为5，则圆的半径为（ ）.A、16或6 B、3或8 C、3 D、83. 已知⊙O的半径是4，点P到圆心O的距离OP＝3，则点P与⊙O的位置关系是（ ）A、点P在⊙O外 B、点P在⊙O上 C、点P在⊙O内 D、不能确定4. 如图所示，在半径为10cm的⊙O中，弦AB＝16cm ， OC⊥AB于点C ， 则OC等于（ ）
A、3cm B、4cm C、5cm D、6cm5. 在 中，直径AB＝15，弦DE⊥AB于点C．若OC：OB＝3 ：5，则DE的长为（ ）A、6 B、9 C、12 D、156. 往直径为 的圆柱形容器内装入一些水以后，截面如图所示，若水面宽 ，则水的最大深度为（ ）
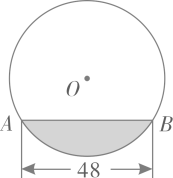A、 B、 C、 D、7. 如图，OA、OB是⊙O的半径，点C在⊙O上，连接AC、BC ， 若∠A=20°，∠B=70°，则∠ACB的度数为（ ）
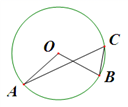A、50° B、55° C、60° D、65°8. 半径为10的 中，弦 ，则点O到弦AB的距离为A、10 B、8 C、6 D、59. 小明家的圆形玻璃打碎了，其中三块碎片如图所示，为了配到与原来大小一样的圆形玻璃，小明应带到商店去的一块碎片是（ ）
A、① B、② C、③ D、均不可能10. 在Rt△ABC中， ∠C=90°,AC=3cm， AB=5cm,若以C为圆心，4cm为半径画一个圆，则下列结论中，正确的是（ ）A、点A在圆C内，点B在圆C外 B、点A在圆C外，点B在圆C内 C、点A在圆C上，点B在圆C外 D、点A在圆C内，点B在圆C上二、填空题
-
11. 如图，MN是⊙O的直径，矩形ABCD的顶点A、D在MN上，顶点B、C在⊙O上，若⊙O的半径为5，AB=4，则BC边的长为 ．
12. 下列语句错误的有 ．①直径是弦； ②优弧一定大于劣弧； ③长度相等的弧是等弧； ④平分弦的直径垂直于弦； ⑤半圆是弧．
13. 已知直线l：y＝x+1，点A（1，0），点B（0，-2），设点P为直线l上一动点，当点P的坐标为时，过P、A、B不能作出一个圆．14. 战国时期的数学家墨子撰写的《墨经》一书中，就有“圆，一中同长也”的记载，这句话中的“中”字的意思可以理解为15. 如图，AB为 的直径，弦 于点H ， 若 ， ，则OH的长度为 ．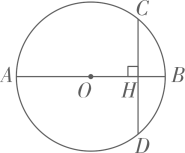
16. 我们知道，两点之间线段最短，因此，连接两点间线段的长度叫做两点间的距离；同理，连接直线外一点与直线上各点的所有线段中，垂线段最短，因此，直线外一点到这条直线的垂线段的长度，叫做点到直线的距离．类似地，连接曲线外一点与曲线上各点的所有线段中，最短线段的长度，叫做点到曲线的距离．依此定义，如图，在平面直角坐标系中，点 到以原点为圆心，以1为半径的圆的距离为 ．
17. 我国古代数学经典著作《九章算术》中记载了一个“圆材埋壁”的问题：“今有圆材埋在壁中，不知大小.以锯锯之，深一寸，锯道长一尺.问径几何？”意思是：今有一圆柱形木材，埋在墙壁中，不知其大小.用锯去锯这木材，锯口深 寸，锯道长 尺（1尺=10寸）.问这根圆形木材的直径是寸.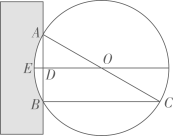
18. 已知⊙O的直径为10cm，AB，CD是⊙O的两条弦， ， ， ，则 与 之间的距离为cm.三、解答题
-
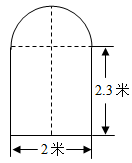
19. 有一辆载有集装箱的卡车，高2.5米，宽1.6米，要开进如图所示的上边是半圆，下边是长方形的桥洞，已知半圆的直径为2米，长方形的另一条边长是2.3米，这辆卡车能否通过此桥洞？通过计算说明理由.
20. 筒车是我国古代发明的一种水利灌溉工具，彰显了我国古代劳动人民的智慧，图 ，点 表示筒车的一个盛水桶．如图 ，当筒车工作时，盛水桶的运行路径是以轴心 为圆心， 为半径的圆，且圆心在水面上方．若圆被水面截得的弦 长为 ，求筒车工作时，盛水桶在水面以下的最大深度．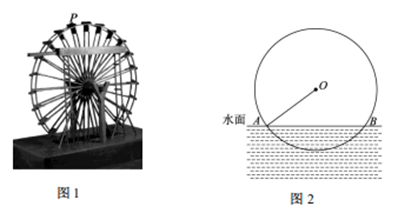
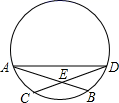
21. 如图，A，B是⊙O上两点，∠AOB=120°，C为弧AB的中点，求证：四边形OACB是菱形.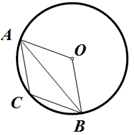
22. 如图，已知A、B、C、D四点在⊙O上，AB、CD交于点E ， AD＝BC ， 求证：AB＝CD ．
23. 《九章算术》是中国传统数学重要的著作，奠定了中国传统数学的基本框架．《九章算术》中记载：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，间径几何？”（如图①）
阅读完这段文字后，小智画出了一个圆柱截面示意图（如图②），其中BO⊥CD于点A，求间径就是要求⊙O的直径．
再次阅读后，发现AB=（ ）寸，CD=（ ）寸（一尺等于十寸），通过运用有关知识即可解决这个问题．请你补全题目条件，并帮助小智求出⊙O的直径．
