初中数学苏科版八年级上学期期中复习专题9 勾股定理的应用
试卷更新日期：2020-10-26 类型：复习试卷
一、单选题
-
1. 如图，由于受台风的影响，一颗大树在离地面6 m处折断，顶端落在离树干底部8 m处，则这棵树在折断前的高度是（ ）
A、8m B、10m C、16m D、18m2. 如图，斜靠在墙上的一根竹竿，AB=5m，OB=3m。若B端沿地面OB方向外移0.5m，则A端沿垂直于地面AC方向下移（ ）
A、等于0.5m B、小于0.5m C、大于0.5m D、不确定3. 如图，圆柱的高为8cm，底面半径为 cm，一只蚂蚁从点A沿圆柱外壁爬到点B处吃食，要爬行的最短路程是（ ）
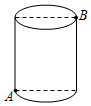A、6cm B、8cm C、10cm D、12cm4. 如图，有一个水池，其底面是边长为16尺的正方形，一根芦苇AB生长在它的正中央，高出水面部分BC的长为2尺，如果把该芦苇沿与水池边垂直的方向拉向岸边，那么芦苇的顶部B恰好碰到岸边的B′，则这根芦苇AB的长是（ ）
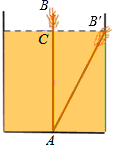A、15尺 B、16尺 C、17尺 D、18尺5. 将一根 24cm 的筷子，置于底面直径为 15cm ， 高 8cm 的装满水的无盖圆柱形水杯中，设筷子浸没在杯子里面的长度为 hcm ， 则 h 的取值范围是（ ）A、h≤15cm B、h≥8cm C、8cm≤h≤17cm D、7cm≤h≤16cm6. 勾股定理是人类最伟大的科学发现之一，在我国古算书《周髀算经》中早有记载.如图1，以直角三角形的各边为边分别向外作正方形，再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若图2中阴影部分的面积为2，且AB+AC=8，则BC的长为（ ）
A、4 B、6 C、 D、7. 一艘轮船以16海里/小时的速度从港口A出发向东北方向航行，同时另一轮船以12海里/小时从港口A出发向东南方向航行，离开港口3小时后，则两船相距（ ）A、36海里 B、48海里 C、60海里 D、84海里8. 如图，正方体的棱长为6cm，A是正方体的一个顶点，B是侧面正方形对角线的交点.一只蚂蚁在正方体的表面上爬行，从点A爬到点B的最短路径是（ ）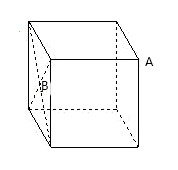
A、9 B、 C、 D、129. 公元3世纪初，中国古代数学家赵爽注《周髀算经》时，创造了“赵爽弦图”．如图，设勾a＝6，弦c＝10，则小正方形ABCD的面积是（ ）
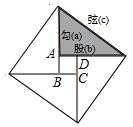A、4 B、6 C、8 D、1610. 如图，架在消防车上的云梯AB长为10m，∠ADB=90°，AD=2BD，云梯底部离地面的距离BC为2m，则云梯的顶端离地面的距离AE为（ ）
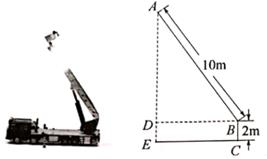A、(2 +2)m B、(4 +2)m C、(5 +2)m D、7m二、填空题
-
11. 如图，为修铁路需凿通隧道BC ， 测得∠C＝90°，AB＝5km ， AC＝4km ， 若每天凿隧道0.3km ， 则需天才能把隧道凿通．
12. 如图1，直角三角形纸片的一条直角边长为2，剪四块这样的直角三角形纸片，把它们按图2放入一个边长为3的正方形中(片在结合部分不重叠无缝隙)，则图2中阴影部分面积为。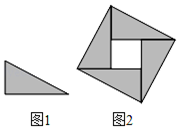
13. 如图，圆柱形玻璃板，高为12cm，底面周长为18cm，在杯内离杯底3cm的点C处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿3cm与蜂蜜相对的A处，则蚂蚁到达蜂蜜的最短距离cm．
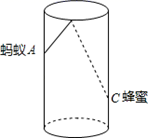14. 活动楼梯如图所示，∠B＝90°，斜坡AC的坡度为1：1，斜坡AC的坡面长度为8m，则走这个活动楼梯从A点到C点上升的高度BC为 ．
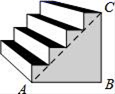15. 如图是高空秋千的示意图，小明从起始位置点A处绕着点O经过最低点B，最终荡到最高点C处，若∠AOC=90°，点A与点B的高度差AD=1米，水平距离BD=4米，则点C与点B的高度差CE为米。
16. 如图，教室的墙面ADEF与地面ABCD垂直，点P在墙面上，若PA=5，AB=8，点P到AD的距离是3，有一只蚂蚁要从点P爬到点B，它的最短行程是.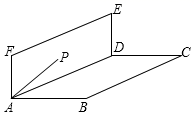
17. 如图所示，“赵爽弦图”是由8个全等的直角三角形拼接而成的，记图中正方形ABCD，正方形EFGH，正方形MNKT的面积分别为 ，已知 ，则 的值是.
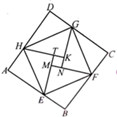18. 《算法统宗》中有一道“荡秋干”的问题，其译文为：“有一架秋千，当它静止时，踏板上一点A离地1尺，将它往前推送10尺(水平距离)时，点A对应的点B就和某人一样高，若此人的身高为5尺，秋干的绳索始终拉得很直，试问绳素有多长？”根据上述条件，秋干绳索长为尺.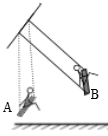
三、解答题
-
19. 如图，一高层住宅发生火灾，消防车立即赶到距大厦9米处（车尾到大厦墙面），升起云梯到火灾窗口，已知云梯长15米，云梯底部距地面2米，问：发生火灾的住户窗口距离地面多高？
20. 如图，AB⊥BC，CD⊥BC，点E在BC上，且AE＝DE. 若AB＝20，CD＝30，BC＝50，求AE的长.
21. 《中华人民共和国道路交通管理条例》规定：小汽车在城市街道上行驶速度不得超过70千米/时，一辆小汽车在一条城市街道上直向行驶，某一时刻正好行驶到距车速检测仪 正前方50米的 处，过了6秒后，测得小汽车的位置 与车速检测仪 之间的距离为130米，这辆小汽车超速了吗？请说明理由.
22. 如图，小巷左右两侧是竖直的墙，一架梯子 斜靠在左墙时，梯子底端到左墙角的距离 为0.7米，顶端到地面距离 为2.4米，如果保持梯子底端位置不动，将梯子斜靠在右墙时，顶端到地面距离 为2米，求小巷的宽度 .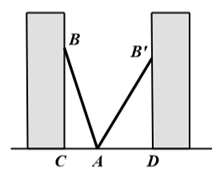
23. 拉杆箱是人们出行的常用品，采用拉杆箱可以让人们出行更轻松.如图，一直某种拉杆箱箱体长AB＝65cm，拉杆最大伸长距离BC＝35cm，在箱体底端装有一圆形滚轮，当拉杆拉到最长时，滚轮的圆心在图中的A处，点A到地面的距离AD＝3cm，当拉杆全部缩进箱体时，滚轮圆心水平向右平移55cm到A′处，求拉杆把手C离地面的距离（假设C点的位置保持不变）.
24. 在一条东西走向河的一侧有一村庄 ，河边原有两个取水点 ，其中 ，由于某种原因，由 到 的路现在已经不通，该村为方便村民取水决定在河边新建一个取水点 在同一条直线上)，并新修一条路 ，测得 千米， 千米， 千米.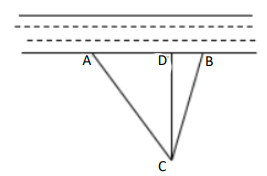
(1)、问 是否为从村庄 到河边最近的路？请通过计算加以说明：(2)、求原来的路线 的长.25. 如图所示，在街道 的同一侧，有两个居民区A，B，两个居民区门口到街道的距离分别为AC，BD.现准备在街道 旁设置一个快递中转站.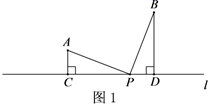
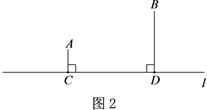
(1)、如果设置的快递中转站到A，B两个小区的距离相等，如图1，当∠A=∠BPD时，请说明AC+BD=CD的理由；(2)、如果设置的快递中转站到A，B两个小区的距离之和最短，请在图2中作出点P的位置，连接AP，BP，直接写出此时∠PAC与∠PBD的数量关系；(3)、为了能错峰进行取送快递，决定设置的快递中转站到A，B两个小区的距离之差最大，请在图3中作出点P的位置，连接AP，BP，直接写出此时∠PAC与∠PBD的数量关系.26. 在直线l上摆放着三个正方形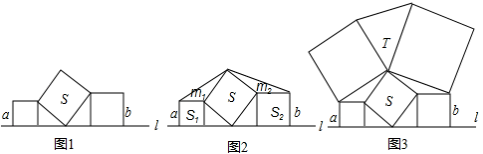
(1)、如图1，已知水平放置的两个正方形的边长依次是a，b斜着放置的正方形的面积S＝ ， 两个直角三角形的面积和为；(均用a，b表示)(2)、如图2，小正方形面积S1＝1，斜着放置的正方形的面积S＝4，求图中两个钝角三角形的面积m1和m2 ， 并给出图中四个三角形的面积关系；(3)、图3是由五个正方形所搭成的平面图，T与S分别表示所在的三角形与正方形的面积，试写出T与S的关系式，并利用(1)和(2)的结论说明理由.