初中数学苏科版八年级上学期期中复习专题8 勾股定理的逆定理
试卷更新日期:2020-10-26 类型:复习试卷
一、单选题
-
1. 三角形的三边长a、b、c满足(a+b)2=c2+2ab,则这个三角形是( )A、等边三角形 B、钝角三角形 C、锐角三角形 D、直角三角形2. 由线段 组成的三角形不是直角三角形的是( )A、 B、 C、 D、3. 如图,方格中的点A,B,C,D,E称为“格点”(格线的交点),以这5个格点中的3点为顶点画三角形,可以画等腰三角形和直角三角形的个数分别是( )
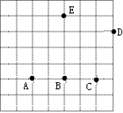 A、2和3 B、3和3 C、2和4 D、3和44. 在△ABC中,BC=5,AC=4,AB=3,则( )A、∠A=90° B、∠B=90° C、∠C=90° D、∠A+∠B=90°5. 满足下列条件的三角形中,不是直角三角形的是( )A、三内角的度数之比为1∶2∶3 B、三内角的度数之比为3∶4∶5 C、三边长之比为3∶4∶5 D、三边长的平方之比为1∶2∶36. 如图, ,且 , , ,则线段 的长为( )
A、2和3 B、3和3 C、2和4 D、3和44. 在△ABC中,BC=5,AC=4,AB=3,则( )A、∠A=90° B、∠B=90° C、∠C=90° D、∠A+∠B=90°5. 满足下列条件的三角形中,不是直角三角形的是( )A、三内角的度数之比为1∶2∶3 B、三内角的度数之比为3∶4∶5 C、三边长之比为3∶4∶5 D、三边长的平方之比为1∶2∶36. 如图, ,且 , , ,则线段 的长为( )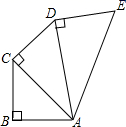 A、1.5 B、2 C、2.5 D、37. 如图,在4×4的正方形网格中,每一格长度为1,小正方形的顶点称为格点,A,B,C,D,E,F都在格点上,以AB,CD,EF为边能构成一个直角三角形,则点F的位置有( )
A、1.5 B、2 C、2.5 D、37. 如图,在4×4的正方形网格中,每一格长度为1,小正方形的顶点称为格点,A,B,C,D,E,F都在格点上,以AB,CD,EF为边能构成一个直角三角形,则点F的位置有( ) A、1处 B、2处 C、3处 D、4处8. 我国古代用勾、股和弦分别表示直角三角形的两条直角边和斜边,如图由四个全等的直角三角形和一个小正方形拼成一个大正方形,数学家邹元治利用该图证明了勾股定理,现已知大正方形面积为9,小正方形面积为5,则每个直角三角形中勾和股的差值为( )
A、1处 B、2处 C、3处 D、4处8. 我国古代用勾、股和弦分别表示直角三角形的两条直角边和斜边,如图由四个全等的直角三角形和一个小正方形拼成一个大正方形,数学家邹元治利用该图证明了勾股定理,现已知大正方形面积为9,小正方形面积为5,则每个直角三角形中勾和股的差值为( ) A、4 B、1 C、2 D、以上都不对9. 下列三角形是直角三角形的是( )A、
A、4 B、1 C、2 D、以上都不对9. 下列三角形是直角三角形的是( )A、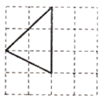 B、
B、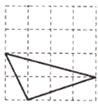 C、
C、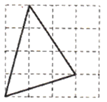 D、
D、 10. 如图,在正方形ABCD纸片上有一点P,PA=1,PD=2,PC=3,现将△PCD剪下,并将它拼到如图所示位置(C与A重合,P与G重合,D与D重合),则∠APD的度数为( )
10. 如图,在正方形ABCD纸片上有一点P,PA=1,PD=2,PC=3,现将△PCD剪下,并将它拼到如图所示位置(C与A重合,P与G重合,D与D重合),则∠APD的度数为( )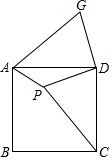 A、150° B、135° C、120° D、108°
A、150° B、135° C、120° D、108°二、填空题
-
11. 2002年8月,在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图1),且大正方形的面积是15,小正方形的面积是3,直角三角形的较短直角边为a,较长直角边为b.如果将四个全等的直角三角形按如图2的形式摆放,那么图2中最大的正方形的面积为.
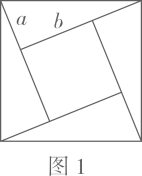
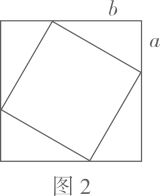 12. 一个三角形的三边的比为5∶12∶13,它的周长为60cm,则它的面积是 .13. 如图,有一四边形空地ABCD,AB⊥AD,AB=3,AD=4,BC=12,CD=13,则四边形ABCD的面积为.
12. 一个三角形的三边的比为5∶12∶13,它的周长为60cm,则它的面积是 .13. 如图,有一四边形空地ABCD,AB⊥AD,AB=3,AD=4,BC=12,CD=13,则四边形ABCD的面积为.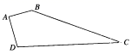 14. 如图:在△ABC中,AB=13,BC=12,点D,E分别是AB,BC的中点,连接DE,CD,如果DE=2.5,那么△ACD的周长是 .
14. 如图:在△ABC中,AB=13,BC=12,点D,E分别是AB,BC的中点,连接DE,CD,如果DE=2.5,那么△ACD的周长是 .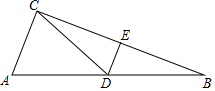 15. 如图,三角形ABC三边的长分别为AB=m2﹣n2 , AC=2mn,BC=m2+n2 , 其中m、n都是正整数.以AB、AC、BC为边分别向外画正方形,面积分别为S1、S2、S3 , 那么S1、S2、S3之间的数量关系为 .
15. 如图,三角形ABC三边的长分别为AB=m2﹣n2 , AC=2mn,BC=m2+n2 , 其中m、n都是正整数.以AB、AC、BC为边分别向外画正方形,面积分别为S1、S2、S3 , 那么S1、S2、S3之间的数量关系为 . 16. 勾股定理是几何中的一个重要定理.在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是把图1放入长方形内得到的, ,AB=3,AC=4,点D,E,F,G,H,I都在长方形KLMJ的边上,则长方形KLMJ的面积为 .
16. 勾股定理是几何中的一个重要定理.在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是把图1放入长方形内得到的, ,AB=3,AC=4,点D,E,F,G,H,I都在长方形KLMJ的边上,则长方形KLMJ的面积为 .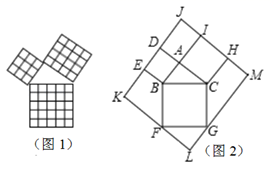
三、解答题
-
17. 如图,在等腰△ABC中,AB=AC=15,点D是AC边上的一点,且CD=3,BD=9,判断 △ABD的形状,并说明理由
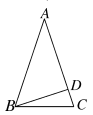 18. 如图,在四边形 中, , , , .
18. 如图,在四边形 中, , , , .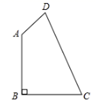
求 的度数.
19. 某中学八(1)班小明在综合实践课上剪了一个四边形ABCD,如图,连接AC,经测量AB=12,BC=9,CD=8,AD=17,∠B=90°.求证:△ACD是直角三角形.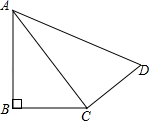 20. 如图,对任意符合条件的直角三角形 ,饶其锐角顶点逆时针旋转90°得 ,所以 ,且四边形 是一个正方形,它的面积和四边形 面积相等,而四边形 面积等于 和 的面积之和,根据图形写出一种证明勾股定理的方法.
20. 如图,对任意符合条件的直角三角形 ,饶其锐角顶点逆时针旋转90°得 ,所以 ,且四边形 是一个正方形,它的面积和四边形 面积相等,而四边形 面积等于 和 的面积之和,根据图形写出一种证明勾股定理的方法. 21. 笔直的河流一侧有一旅游地C,河边有两个漂流点A、B,其中AB=AC,由于某种原因,由C到A的路现在已经不通,为方便游客,决定在河边新建一个漂流点H(A,H,B在一条直线上),并新修一条路CH,测得BC=5千米,CH=4千米,BH=3千米,
21. 笔直的河流一侧有一旅游地C,河边有两个漂流点A、B,其中AB=AC,由于某种原因,由C到A的路现在已经不通,为方便游客,决定在河边新建一个漂流点H(A,H,B在一条直线上),并新修一条路CH,测得BC=5千米,CH=4千米,BH=3千米,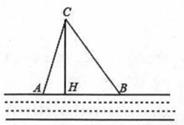 (1)、问CH是否为从旅游地C到河的最近的路线?请通过计算加以说明;(2)、求原来路线AC的长。22.(1)、教材在探索平方差公式时利用了面积法,面积法可以帮助我们直观地推导或验证公式,俗称“无字证明”,例如,著名的赵爽弦图(如图①,其中四个直角三角形较大的直角边长都为a,较小的直角边长都为b,斜边长都为c),大正方形的面积可以表示为c2 , 也可以表示为4× ab+(a-b)2 , 所以4× ab+(a-b)2=c2 , 即a2+b2=c2.由此推导出重要的勾股定理:如果直角三角形两条直角边长为a,b,斜边长为c,则a2+b2=c2.图②为美国第二十任总统伽菲尔德的“总统证法”,请你利用图②推导勾股定理.
(1)、问CH是否为从旅游地C到河的最近的路线?请通过计算加以说明;(2)、求原来路线AC的长。22.(1)、教材在探索平方差公式时利用了面积法,面积法可以帮助我们直观地推导或验证公式,俗称“无字证明”,例如,著名的赵爽弦图(如图①,其中四个直角三角形较大的直角边长都为a,较小的直角边长都为b,斜边长都为c),大正方形的面积可以表示为c2 , 也可以表示为4× ab+(a-b)2 , 所以4× ab+(a-b)2=c2 , 即a2+b2=c2.由此推导出重要的勾股定理:如果直角三角形两条直角边长为a,b,斜边长为c,则a2+b2=c2.图②为美国第二十任总统伽菲尔德的“总统证法”,请你利用图②推导勾股定理.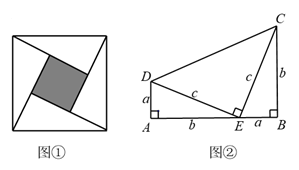
 (2)、试用勾股定理解决以下问题:
(2)、试用勾股定理解决以下问题:如果直角三角形ABC的两直角边长为3和4,则斜边上的高为.
(3)、试构造一个图形,使它的面积能够解释(a-2b)2=a2-4ab+4b2 , 画在上面的网格中,并标出字母a,b所表示的线段.23. 张老师在一次“探究性学习”课中,设计了如下数表:n
2
3
4
5
…
a
22-1
32-1
42-1
52-1
…
b
4
6
8
10
…
c
22+1
32+1
42+1
52+1
…
(1)、请你分别观察a,b,c与n之间的关系,并用含自然数n(n>1)的代数式表示:a= , b= , c=;
(2)、猜想:以a,b,c为边的三角形是否为直角三角形并证明你的猜想.