初中数学苏科版八年级上学期期中复习专题7 勾股定理
试卷更新日期:2020-10-26 类型:复习试卷
一、单选题
-
1. 在△ABC,∠A,∠B,∠C的对应边分别是a,b,c,若∠B=90°,则下列等式中成立的是( )A、a2+b2=c2 B、b2+c2=a2 C、 a2+c2=b2 D、c2- a2= b22. 如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案.现有五种正方形纸片,面积分别是1,2,3,4,5,选取其中三块(可重复选取)按图的方式组成图案,使所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是( )
 A、1,4,5 B、2,3,5 C、3,4,5 D、2,2,43. 如图,在3×3的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,若BD是△ABC的高,则BD的长为( )
A、1,4,5 B、2,3,5 C、3,4,5 D、2,2,43. 如图,在3×3的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,若BD是△ABC的高,则BD的长为( )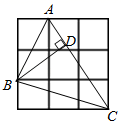 A、 B、 C、 D、4. 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AE平分∠BAC,ED⊥AB,则ED的长( )
A、 B、 C、 D、4. 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AE平分∠BAC,ED⊥AB,则ED的长( )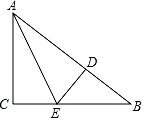 A、3 B、4 C、5 D、65. 直角三角形中,两条直角边长分别是12和5,则斜边中线长是( )A、26 B、13 C、 D、6.56. 2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的弦图,它是由四个全等的直角三角形和中间的小正方形拼成的一个大正方形,如图所示,如果大正方形的面积是34,小正方形的面积是4,直角三角形较短的直角边是a,较长的直角边是b,那么 的值为( )
A、3 B、4 C、5 D、65. 直角三角形中,两条直角边长分别是12和5,则斜边中线长是( )A、26 B、13 C、 D、6.56. 2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的弦图,它是由四个全等的直角三角形和中间的小正方形拼成的一个大正方形,如图所示,如果大正方形的面积是34,小正方形的面积是4,直角三角形较短的直角边是a,较长的直角边是b,那么 的值为( )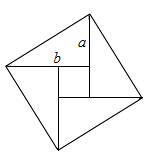 A、 38 B、49 C、52 D、647. 如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,CD⊥AB于D,则CD的长是( )
A、 38 B、49 C、52 D、647. 如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,CD⊥AB于D,则CD的长是( ) A、5 B、7 C、 D、8. 在△ABC中,AB=AC=5,P是BC上异于B,C的一点,则AP2+BP⋅PC的值是( )A、15 B、25 C、30 D、209. 如图所示,已知在三角形纸片ABC中,BC=3,AB=6,∠BCA=90°.在AC上取一点E,以BE为折痕,使AB的一部分与BC重合,A与BC延长线上的点D重合,则DE的长度为( )
A、5 B、7 C、 D、8. 在△ABC中,AB=AC=5,P是BC上异于B,C的一点,则AP2+BP⋅PC的值是( )A、15 B、25 C、30 D、209. 如图所示,已知在三角形纸片ABC中,BC=3,AB=6,∠BCA=90°.在AC上取一点E,以BE为折痕,使AB的一部分与BC重合,A与BC延长线上的点D重合,则DE的长度为( )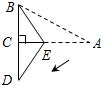 A、6 B、3 C、 D、10. 如图所示,是一张直角三角形的纸片,两直角边AC=6㎝,BC=8㎝,现将△ABC折叠,使点B与点A重合,折痕为DE,则AD的长为( )
A、6 B、3 C、 D、10. 如图所示,是一张直角三角形的纸片,两直角边AC=6㎝,BC=8㎝,现将△ABC折叠,使点B与点A重合,折痕为DE,则AD的长为( )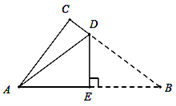 A、4㎝ B、5㎝ C、6㎝ D、 ㎝
A、4㎝ B、5㎝ C、6㎝ D、 ㎝二、填空题
-
11. 如图,在△ABC中,AB=AC,∠BAC的平分线AD交BC于点D,E为AB的中点,若BC=12,AD=8,则DE的长为.
 12. 在 中, ,若 ,则 的长是 .13. 我国古代数学著作《九章算术》中有这样一个问题:“今有池方一丈,葭(jiā)生其中央,出水一尺,引葭赴岸,适与岸齐问水深几何?”(注:丈、尺是长度单位,1丈=10尺)这段话翻译成现代汉语,即为:如图,有一个水池,水面是一个边长为1丈的正方形,在水池正中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面.则水池里水的深度是尺.
12. 在 中, ,若 ,则 的长是 .13. 我国古代数学著作《九章算术》中有这样一个问题:“今有池方一丈,葭(jiā)生其中央,出水一尺,引葭赴岸,适与岸齐问水深几何?”(注:丈、尺是长度单位,1丈=10尺)这段话翻译成现代汉语,即为:如图,有一个水池,水面是一个边长为1丈的正方形,在水池正中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面.则水池里水的深度是尺. 14. 图中阴影部分是一个正方形,则此正方形的面积为cm2.
14. 图中阴影部分是一个正方形,则此正方形的面积为cm2. 15. 如图, , , ,一机器人在点B处看见一个小球从点A出发沿着 方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球,如果小球滚动的速度与机器人行走的速度相等,则机器人行走的路程BC为.
15. 如图, , , ,一机器人在点B处看见一个小球从点A出发沿着 方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球,如果小球滚动的速度与机器人行走的速度相等,则机器人行走的路程BC为.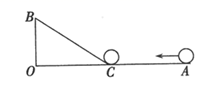 16. 如图,长方体中, , , ,一只蚂蚁从点 出发,以 秒的速度沿长方体表面爬行到点 ,至少需要分钟。
16. 如图,长方体中, , , ,一只蚂蚁从点 出发,以 秒的速度沿长方体表面爬行到点 ,至少需要分钟。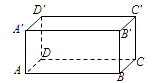
三、解答题
-
17. 小东和小明要测量校园里的一块四边形场地 (如图所示)的周长,其中边 上有水池及建筑遮挡,没有办法直接测量其长度.小东经测量得知 米, 米, .小明说根据小东所得的数据可以求出 的长度.你同意小明的说法吗?若同意,请求出 的长度;若不同意,请说明理由.
 18. 在 中,∠ACB=90°,CD⊥AB于点D , 若BD=9,CD=12,求AB和AC的长.
18. 在 中,∠ACB=90°,CD⊥AB于点D , 若BD=9,CD=12,求AB和AC的长.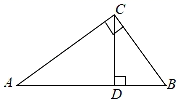 19. 如图,把长方形纸片ABCD沿EF折叠后.点D与点B重合,点C落在点C′的位置上.若∠1=60°,AE=1.
19. 如图,把长方形纸片ABCD沿EF折叠后.点D与点B重合,点C落在点C′的位置上.若∠1=60°,AE=1.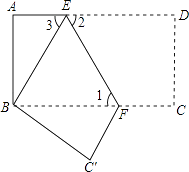 (1)、求∠2、∠3的度数;(2)、求长方形纸片ABCD的面积S.20. 如图,在 Rt△ABC,∠ACB=90°,AC=BC,分别过A、B作直线
(1)、求∠2、∠3的度数;(2)、求长方形纸片ABCD的面积S.20. 如图,在 Rt△ABC,∠ACB=90°,AC=BC,分别过A、B作直线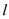 的垂线,垂足分别为M、N.
的垂线,垂足分别为M、N. (1)、求证:△AMC≌△CNB;(2)、若AM=3,BN=5,求AB的长.21. 如图,在△ABC中,∠BAC=90°,AB=6cm,BC=10cm,点D在线段AC上,且CD=2cm,动点P从BA的延长线上距A点10cm的E点出发,以每秒2cm的速度沿射线EA的方向运动了 秒。
(1)、求证:△AMC≌△CNB;(2)、若AM=3,BN=5,求AB的长.21. 如图,在△ABC中,∠BAC=90°,AB=6cm,BC=10cm,点D在线段AC上,且CD=2cm,动点P从BA的延长线上距A点10cm的E点出发,以每秒2cm的速度沿射线EA的方向运动了 秒。 (1)、求AD的长;
(1)、求AD的长;
(2)、直接写出用含有 的代数式表示PE=;(3)、在运动过程中,是否存在某个时刻,使△ABC与△ADP全等?若存在,请求出 值;若不存在,请说明理由.