初中数学苏科版八年级上学期期中复习专题5 线段、角的轴对称性
试卷更新日期：2020-10-26 类型：复习试卷
一、单选题
-
1. 如图，在Rt△ABC中，∠C＝90°，AD是∠BAC的平分线．若AC＝6，AB＝10，则S△ABD：S△ACD为（ ）
A、5：3 B、5：4 C、4：3 D、3：52. 如图所示，在Rt△ABC中，∠BAC=90°，AB=8，AC=6，DE是AB边的垂直平分线，垂足为D，交边BC于点E，则△ACE的周长为（ ）
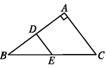A、16 B、15 C、14 D、133. 如图，△ABC中，AB的垂直平分线交BC边于点E，AC的垂直平分线交BC边于点N，若∠BAC＝70°，则∠EAN的度数为（ ）
A、35° B、40° C、50° D、55°4. 如图，△ABC中，AB=6cm ， AC=8cm，BC的垂直平分线l与AC相交于点D ， 则△ABD的周长为（ ）
A、10 cm B、12 cm C、14 cm D、16 cm5. 如图，在△ABE中，AE的垂直平分线MN交BE于点C，∠E＝30°，且AB＝CE，则∠BAE的度数是（ ）
A、80° B、85° C、90° D、105°6. 如图，在△ABC中，∠C=90°，AD平分∠BAC，DE⊥AB于E，下列结论：①CD=ED；②AC+BE=AB；③∠BDE=∠BAC；④BE=DE；⑤S△BDE：S△ACD=BD：AC，其中正确的个数（ ）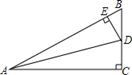
A、5个 B、4个 C、3个 D、2个7. 如图，已知在 中， ， 的垂直平分线 交 于点E， 的垂直平分线正好经过点B，与 相交于点F，则 的度数是（ ）
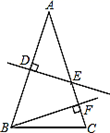A、30° B、36° C、45° D、35°8. 如图，射线OC是∠AOB的角平分线，D是射线OC上一点，DP⊥OA于点P ， DP＝4，若点Q是射线OB上一点，OQ＝3，则△ODQ的面积是（ ）
A、3 B、4 C、5 D、69. 如图，△ABC中，AB＝AC，AD是∠BAC的角平分线，AC的垂直平分线分别交AC，AD，AB于点E，O，F，则下列结论不一定成立的是（ ）
A、AD⊥BC B、OC+OD＝AD C、OA＝OB D、∠ACO＝∠BOF10. 如图，已知：在△ABC中，AB、BC边上的垂直平分线相交于点P．若∠BAC=50°，则∠BPC的度数为（ ）
A、100° B、110° C、115° D、120°二、填空题
-
11. 如图，BD是∠ABC的角平分线，DE⊥AB于E，△ABC的面积是15cm2，AB＝9cm，BC＝6cm，则DE＝cm．
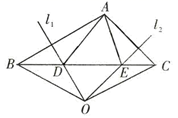
12. 如图，线段AB、BC的垂直平分线 、 相交于点O，若 39°，则 =.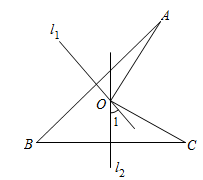
13. 如图，点P是 的角平分线上一点， ，垂足为点D，且 ，点M是射线 上一动点，则 的最小值为 ．
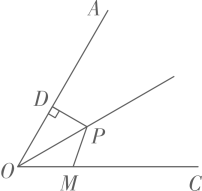14. 如图，在△ABC中，若PM，QN分别垂直平分AB，AC，如果BC=10cm，则△APQ的周长为
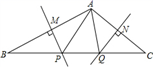15. 已知： 平分 ， 平分 ， 于点 ， 的周长是12，面积是6，则 的长是：.
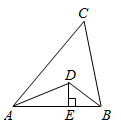16. 已知：如图，BD为△ABC的角平分线，且BD=BC，E为BD延长线上的一点，BE=BA，过E作EF⊥AB，F为垂足，下列结论：①△ABD≌△EBC；②∠BCE+∠BCD=180°；③AD=EF=EC；④BA+BC=2BF，其中正确的结论有（填序号）．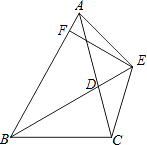
三、解答题
-
17. 某地有两条相交叉的公路， 计划修建一个饭馆：希望饭馆点P既在MN这条公路上，又到直线OA、OB的距离相等．你能确定饭馆应该建在什么位置吗？（保留作图痕迹）
18. 如图，在四边形 中， ，点E，F分别在 ， 上， ， ，求证： .
19. 如图，△ABC中，∠CAB的平分线与BC的垂直平分线DG相交于D，过点D作DE⊥AB，DF⊥AC，求证：BE＝CF．
20. 如图，OC是∠AOB的角平分线，P是OC上一点，PD⊥OA，PE⊥OB，垂足分别为D，E.F是OC上另一点，连接DF，EF.求证：DF=EF.
21. 如图：△ABC中，DE是BC边的垂直平分线，垂足为E，AD平分∠BAC且MD⊥AB，DN⊥AC延长线于N.求证：BM=CN.
22.已知：如图，△ABC中，∠C=90°，BD平分∠ABC交AC于点D，AB边的垂直平分线EF交BD于点E，连AE
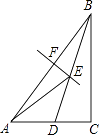(1)、比较∠AED与∠ABC的大小关系，并证明你的结论(2)、若△ADE是等腰三角形，求∠CAB的度数．
