初中数学苏科版八年级上学期期中复习专题3 全等三角形的判定
试卷更新日期:2020-10-26 类型:复习试卷
一、单选题
-
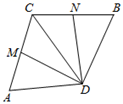
1. 如图,CA=CB , AD=BD , M、N分别为CA、CB的中点,∠ADN=80°,∠BDN=30°,则∠CDN的度数为( )
 A、40° B、15° C、25° D、30°2. 如图,点E,点F在直线AC上, AE=CF, AD=CB,下列条件中不能判断△ADF≌△CBE的是( )
A、40° B、15° C、25° D、30°2. 如图,点E,点F在直线AC上, AE=CF, AD=CB,下列条件中不能判断△ADF≌△CBE的是( ) A、AD//BC B、BE//DF C、BE=DF D、∠A=∠C3. 如图,△ABC中,AB=AC ,点D , E分别在AB , AC上,添加下列条件后,不能判定△ABE≌△ACD的是( )
A、AD//BC B、BE//DF C、BE=DF D、∠A=∠C3. 如图,△ABC中,AB=AC ,点D , E分别在AB , AC上,添加下列条件后,不能判定△ABE≌△ACD的是( )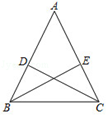 A、AD=AE B、BE=CD C、∠ADC=∠AEB D、∠DCB=∠EBC4. 如图,已知 , ,添加下列条件仍不能证明 的是( )
A、AD=AE B、BE=CD C、∠ADC=∠AEB D、∠DCB=∠EBC4. 如图,已知 , ,添加下列条件仍不能证明 的是( )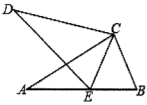 A、 B、 C、 D、5. 下列条件中能判定 的是( )A、 B、 C、 D、6. 如图,已知△ABC的六个元素,则下列甲、乙、丙三个三角形中和△ABC全等的图形是( )
A、 B、 C、 D、5. 下列条件中能判定 的是( )A、 B、 C、 D、6. 如图,已知△ABC的六个元素,则下列甲、乙、丙三个三角形中和△ABC全等的图形是( )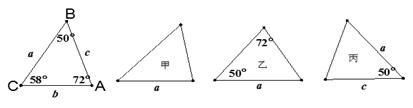 A、甲 B、乙与丙 C、丙 D、乙7. 如图,点E,F在BD上,AD=BC,DF=BE,添加下面四个条件中的一个,使△ADE≌△CBF的是( )
A、甲 B、乙与丙 C、丙 D、乙7. 如图,点E,F在BD上,AD=BC,DF=BE,添加下面四个条件中的一个,使△ADE≌△CBF的是( )①∠A=∠C;②AE=CF;③∠D=∠B;④AE∥CF.
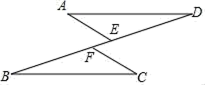 A、①或③ B、①或④ C、②或④ D、②或③8. 如图,△ 中, 、 的角平分线 、 交于点 ,延长 、 , , ,则下列结论中正确的个数是( )
A、①或③ B、①或④ C、②或④ D、②或③8. 如图,△ 中, 、 的角平分线 、 交于点 ,延长 、 , , ,则下列结论中正确的个数是( )①CP平分∠ACF;②∠ABC+2∠APC=180°;③∠ACB=2∠APB④若PM⊥BE,PN⊥BC,则AM+CN=AC;
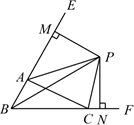 A、1个 B、2个 C、3个 D、4个9. 如图,已知等边 和等边 ,点 在 的延长线上, 的延长线交 于点M , 连 ,若 ,则 ( )
A、1个 B、2个 C、3个 D、4个9. 如图,已知等边 和等边 ,点 在 的延长线上, 的延长线交 于点M , 连 ,若 ,则 ( )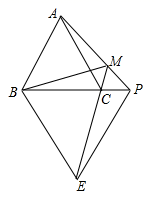 A、 B、 C、 D、10. 如图,已知△ABE与△CDE都是等腰直角三角形,∠AEB=∠DEC=90°,连接AD,AC,BC,BD,若AD=AC=AB,则下列结论:①AE垂直平分CD,②AC平分∠BAD,③△ABD是等边三角形,④∠BCD的度数为150°,其中正确的个数是( )
A、 B、 C、 D、10. 如图,已知△ABE与△CDE都是等腰直角三角形,∠AEB=∠DEC=90°,连接AD,AC,BC,BD,若AD=AC=AB,则下列结论:①AE垂直平分CD,②AC平分∠BAD,③△ABD是等边三角形,④∠BCD的度数为150°,其中正确的个数是( )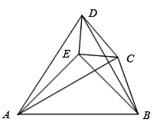 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 如图,已知在△ABD和△ABC中,∠DAB=∠CAB , 点A、B、E在同一条直线上,若使△ABD≌△ABC , 则还需添加的一个条件是 . (只填一个即可)
 12. 如图,AB=AD,只需添加一个条件 , 就可以判定△ABC≌△ADE.
12. 如图,AB=AD,只需添加一个条件 , 就可以判定△ABC≌△ADE.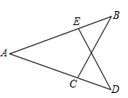 13. 如图,已知AC与BF相交于点E , AB∥CF , 点E为BF中点,若CF=6,AD=4,则BD= .
13. 如图,已知AC与BF相交于点E , AB∥CF , 点E为BF中点,若CF=6,AD=4,则BD= .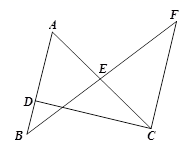 14. 如图,某同学把一块三角形的玻璃打破成了三块,现要到玻璃店去配一块大小、形状完全相同的玻璃,那么他可以带那一块 .
14. 如图,某同学把一块三角形的玻璃打破成了三块,现要到玻璃店去配一块大小、形状完全相同的玻璃,那么他可以带那一块 . 15. 如图,在Δ 中,已知 点 为 中点,点 在线段 上以每秒 的速度由 点向 点运动,同时点 在线段 上由 点向 点运动。当点 的运动速度为每秒 时,能够在某一时刻使得Δ 与Δ 全等
15. 如图,在Δ 中,已知 点 为 中点,点 在线段 上以每秒 的速度由 点向 点运动,同时点 在线段 上由 点向 点运动。当点 的运动速度为每秒 时,能够在某一时刻使得Δ 与Δ 全等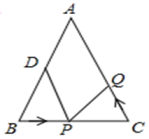 16. 如图,AD=BD,AD⊥BC,垂足为D,BF⊥AC,垂足为F,BC=6cm,DC=2cm,则AE=cm.
16. 如图,AD=BD,AD⊥BC,垂足为D,BF⊥AC,垂足为F,BC=6cm,DC=2cm,则AE=cm.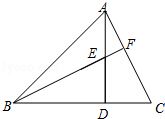 17. 如图,在正方形网格中,每个小正方形的边长均为1,每个小正方形顶点叫做格点,△ABC的顶点都在格点上,以AB为一边作△ABP,使之与△ABC全等,从 、 、 、 四点中找出符合条件的点P,则点P有个
17. 如图,在正方形网格中,每个小正方形的边长均为1,每个小正方形顶点叫做格点,△ABC的顶点都在格点上,以AB为一边作△ABP,使之与△ABC全等,从 、 、 、 四点中找出符合条件的点P,则点P有个 18. 如图,在锐角△ABC中,AB=4 ,∠BAC=45°,∠BAC的平分线交BC于点D , M、N分别是AD和AB上的动点,则BM+MN的最小值是 .
18. 如图,在锐角△ABC中,AB=4 ,∠BAC=45°,∠BAC的平分线交BC于点D , M、N分别是AD和AB上的动点,则BM+MN的最小值是 .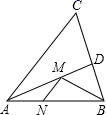
三、解答题
-
19. 已知:AB=AC , AF=AG , AE⊥BG交BG的延长线于E , AD⊥CF交CF的延长线于D . 求证:AD=AE .
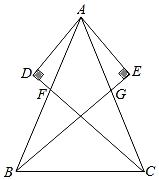 20. 如图,已知AB=AE , AC=AD , ∠BAD=∠EAC . 求证:∠B=∠E .
20. 如图,已知AB=AE , AC=AD , ∠BAD=∠EAC . 求证:∠B=∠E .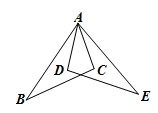 21. 已知:如图, , ,连接 、 相交于点 ,点 、 在线段 上,且 ,求证: .
21. 已知:如图, , ,连接 、 相交于点 ,点 、 在线段 上,且 ,求证: .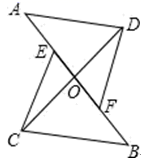
四、综合题
-
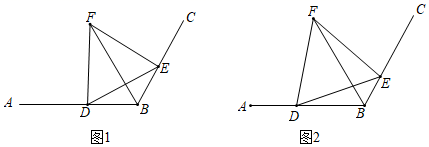
22. 在∠MAN内有一点D,过点D分别作DB⊥AM,DC⊥AN,垂足分别为B,C.且BD=CD,点E,F分别在边AM和AN上.
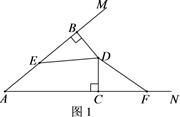
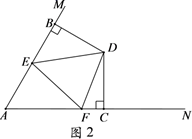 (1)、如图1,若∠BED=∠CFD,请说明DE=DF;(2)、如图2,若∠BDC=120°,∠EDF=60°,猜想EF,BE,CF具有的数量关系,并说明你的结论成立的理由.23. 如图,在Rt△ABC中,∠ACB=90°,AC=BC , 点D在边BC上(不与点B、C重合),BE⊥AD , 重足为E , 过点C作CF⊥CE , 交线段AD于点F .
(1)、如图1,若∠BED=∠CFD,请说明DE=DF;(2)、如图2,若∠BDC=120°,∠EDF=60°,猜想EF,BE,CF具有的数量关系,并说明你的结论成立的理由.23. 如图,在Rt△ABC中,∠ACB=90°,AC=BC , 点D在边BC上(不与点B、C重合),BE⊥AD , 重足为E , 过点C作CF⊥CE , 交线段AD于点F .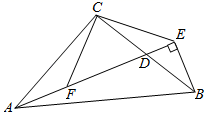 (1)、试说明△CAF≌△CBE的理由;(2)、数学老师在课堂上提出一个问题,如果EF=2AF , 试说明CD=BD的理由.班级同学随后进行了热烈讨论,小明同学提出了自己的想法,可以取EF的中点H , 联结CH , 就能得出结论,你能否能根据小明同学的想法,写出CD=BD的理由.
(1)、试说明△CAF≌△CBE的理由;(2)、数学老师在课堂上提出一个问题,如果EF=2AF , 试说明CD=BD的理由.班级同学随后进行了热烈讨论,小明同学提出了自己的想法,可以取EF的中点H , 联结CH , 就能得出结论,你能否能根据小明同学的想法,写出CD=BD的理由.