初中数学苏科版八年级上学期期中复习专题2 全等三角形的性质
试卷更新日期：2020-10-26 类型：复习试卷
一、单选题
-
1. 已知△ABC≌△DEF，点A与D，点C与F分别是对应点，则∠B的对应角是（ ）A、∠A B、∠F C、∠E D、∠C2. 如图，若△ABC≌△ADE，则下列结论中一定成立的是（ ）
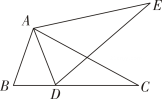A、AC＝DE B、∠BAD＝∠CAE C、AB＝AE D、∠ABC＝∠AED3. 如图，△ ≌△ ，那么下列结论错误的是（ ）
A、 B、 C、 ∥ D、 ∥4. 如图， ，A和D，B和E是对应点，B，C，D在同一直线上，且CE＝5，AC＝7，则BD的长为（ ）
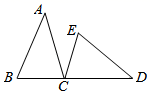A、12 B、7 C、2 D、145. 如图，锐角△ABC中，D，E分别是AB，AC边上的点，△ADC≌△ADC′，△AEB≌△AEB′，且C′D∥EB′∥BC，BE，CD交于点F．若∠BAC＝35°，则∠BFC的大小是（ ）
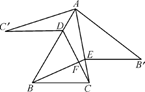A、106° B、108° C、110° D、112°6. 如图，△ABC≌△A ' B ' C，∠BCB ' =30°则∠ACA ' 的度数为 （）
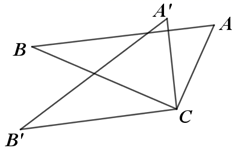A、30° B、45° C、60° D、15°7. 如图，在 中， ， 的角平分线 ， 相交于点P，过点P作 交 的延长线于点F，交 于点H．则下列结论：① ；② ；③ ；④连接 ， 平分 ．其中正确的是（ ）．
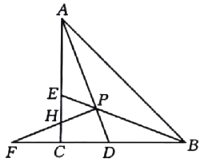A、①②③ B、①②④ C、①③④ D、①②③④8. 如图，在 的网格中，每一个小正方形的边长都是1，点 ， ， ， 都在格点上，连接 ， 相交于 ，那么 的大小是（ ）
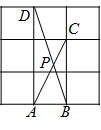A、 B、 C、 D、9. 如图，点O在AD上，∠A＝∠C，∠AOC＝∠BOD， AB＝CD，AD＝6，OB＝2，则OC的长为（ ）
A、2 B、3 C、4 D、610. 如图，点P在∠MAN的角平分线上，点B，C分别在AM，AN上，作PR⊥AM，PS⊥AN，垂足分别是R，S．若∠ABP+∠ACP=180°，则下面三个结论：①AS=AR；②PC∥AB；③△BRP≌△CSP．其中正确的是（ ）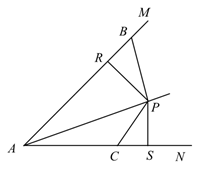
A、①② B、②③ C、①③ D、①②③二、填空题
-
11. 如图，在 和 中， ， ， ，则 º．
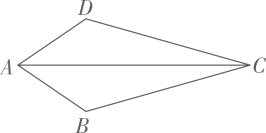12. 已知 ， ， 的面积是 ，那么 中 边上的高是 .13. 如图，在△ABC中，AD⊥DE，BE⊥DE，AC、BC分别平分∠BAD和∠ABE．点C在线段DE上．若AD=5，BE=2，则AB的长是 ．
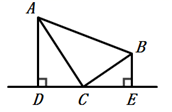14. 已知：如图所示，CE、CB分别是△ABC与△ADC的中线，且AC＝AB．则下列结论中：①BC＝BD；②∠ECB＝∠BCD；③∠ACE＝∠BDC；④CD＝2CE；符合题意结论的序号为： ．
15. 如图，已知AC与BF相交于点E ， AB∥CF ， 点E为BF中点，若CF=6，AD=4，则BD= ．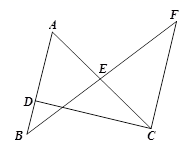
16. 如图，点D、M、N分别为△AEB与△AFC的边与边的交点，AE⊥BE，AF⊥CF，垂足分别为E、F，AE=AF，BE=CF，则下列各个结论中：①∠EAF=90°；②CN=BM；③AN=BN；④△MCD≌△NBD．其中正确结论的序号为 ．
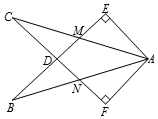17. 如图，点C在线段AB上，DA⊥AB ， EB⊥AB ， FC⊥AB ， 且DA＝ BC ， EB＝AC ， FC＝AB ， ∠AFB＝50°，则∠DFE＝ ．
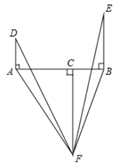18. 如图，在△ABC中，∠ACB=90∘ ， BC=4，AC=3，线段PQ⊥BC于Q(如图，此时点Q与点B重合)，PQ=AB，当点P沿PB向B滑动时，点Q相应的从B沿BC向C滑动，始终保持PQ=AB不变，当△ABC与△PBQ全等时，PB的长度等于.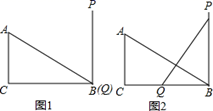
三、解答题
-
19. 如图，△ABC≌△ADE，且∠CAD=35°，∠B=∠D=20°，∠EAB=105°，求∠BFD和∠BED的度数.
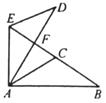20. 如图，AC是∠BAE的平分线，点D是线段AC上的一点，∠C＝∠E，AB＝AD.求证：BC＝DE.
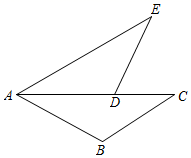21. 两个大小不同的等腰直角三角形三角板如图1所示放置，图2是由它抽象出的几何图形，B，C，E在同一条直线上，连结 .请猜想： 与 的数量及位置关系，并说明理由.
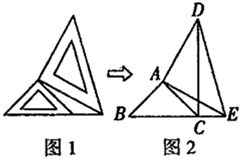22. 如图，已知：△ABC中，AB=AC，∠BAC=90°，分别过B，C向经过点A的直线EF作垂线，垂足为E，F.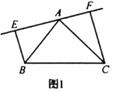
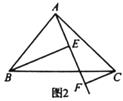
(1)、当EF与斜边BC不相交时，请证明EF=BE+CF（如图1）；(2)、如图2，当EF与斜边BC这样相交时，其他条件不变，证明：EF=BE－CF；(3)、如图3，当EF与斜边BC这样相交时，猜想EF、BE、CF之间的关系，不必证明.23. 如图，在等边三角形ABC中，点E是边AC上一定点，点D是直线BC上一动点，以DE为一边作等边三角形DEF，连接CF．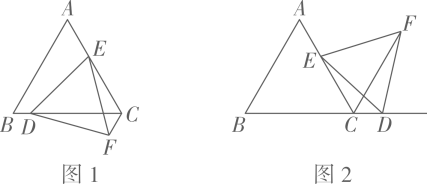
(1)、（问题解决）如图1，若点D在边BC上，求证：CE+CF＝CD；
(2)、（类比探究）如图2，若点D在边BC的延长线上，请探究线段CE，CF与CD之间存在怎样的数量关系？并说明理由．
24. 已知∠ACD＝60°，AC＝DC，MN是过点A的直线，B、E两点在直线MN上，∠BCE＝60°，CB＝CE.
(1)、问题发现：如图1，BD和EA之间的数量关系为 ， BD、AB、BE之间的数量关系为；(2)、拓展探究：当MN绕点A旋转到如图2位置时，BD、AB、BE之间满足怎样的数量关系？请写出你的猜想，并给予证明.(3)、解决问题：当MN绕点A分别旋转到如图2和如图3位置时，若当时∠CAN＝50°，连接AD，则∠ADB的大小为.