浙江省余姚市2019-2020学年八年级上学期数学期末考试试卷
试卷更新日期:2020-10-26 类型:期末考试
一、选择题
-
1. 下面四个图是“余姚阳明故里 征集大赛”的四件作品,其中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 在平面直角坐标系中,点(-1, 2)所在的象限是 ( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 已知一个等腰三角形的底角为 ,则这个三角形的顶角为( )A、 B、 C、 D、4. 下列选项错误的是( )A、若 , ,则 B、若 ,则 C、若 ,则 D、若 ,则5. 下列平面直角坐标系中的图象,不能表示 是 的函数是( )A、
2. 在平面直角坐标系中,点(-1, 2)所在的象限是 ( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 已知一个等腰三角形的底角为 ,则这个三角形的顶角为( )A、 B、 C、 D、4. 下列选项错误的是( )A、若 , ,则 B、若 ,则 C、若 ,则 D、若 ,则5. 下列平面直角坐标系中的图象,不能表示 是 的函数是( )A、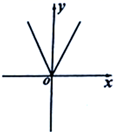 B、
B、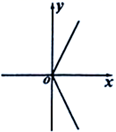 C、
C、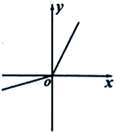 D、
D、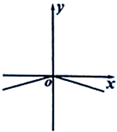 6. 下列尺规作图分别表示:①作一个角的平分线;②作一个角等于已知角;③作一条线段的垂直平分线.其中作法正确的是( )
6. 下列尺规作图分别表示:①作一个角的平分线;②作一个角等于已知角;③作一条线段的垂直平分线.其中作法正确的是( )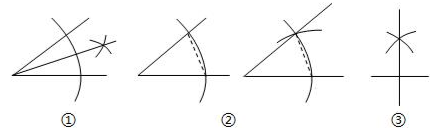 A、①② B、①③ C、②③ D、①②③7. 能说明命题“对于任意正整数 ,则 ”是假命题的一个反例可以是( )A、 B、 C、 D、8. 若 , , 为 的三边长,则下列条件中不能判定 是直角三角形的是( )A、 , , B、 C、 D、9. 如图,有一张直角三角形纸片, , , ,现将 折叠,使边 与 重合,折痕为 ,则 的长为( )
A、①② B、①③ C、②③ D、①②③7. 能说明命题“对于任意正整数 ,则 ”是假命题的一个反例可以是( )A、 B、 C、 D、8. 若 , , 为 的三边长,则下列条件中不能判定 是直角三角形的是( )A、 , , B、 C、 D、9. 如图,有一张直角三角形纸片, , , ,现将 折叠,使边 与 重合,折痕为 ,则 的长为( )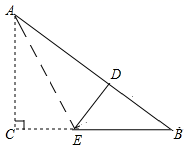 A、 B、 C、 D、10. 如图, 是等边三角形, 是边 上一点,且 的度数为 ,则 的值可能是( )
A、 B、 C、 D、10. 如图, 是等边三角形, 是边 上一点,且 的度数为 ,则 的值可能是( )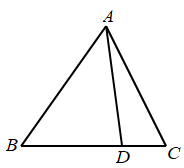 A、10 B、20 C、30 D、4011. 某天,某同学早上8点坐车从余姚图书馆出发去宁波大学,汽车离开余姚图书馆的距离 (千米)与所用时间 (分)之间的函数关系如图所示.已知汽车在途中停车加油一次,则下列描述不正确的是( )
A、10 B、20 C、30 D、4011. 某天,某同学早上8点坐车从余姚图书馆出发去宁波大学,汽车离开余姚图书馆的距离 (千米)与所用时间 (分)之间的函数关系如图所示.已知汽车在途中停车加油一次,则下列描述不正确的是( )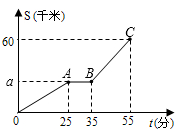 A、汽车在途中加油用了10分钟 B、若 ,则加满油以后的速度为80千米/小时 C、若汽车加油后的速度是90千米/小时,则 D、该同学 到达宁波大学12. 如图,点 , , , 顺次在直线 上,以 为底边向下作等腰直角三角形 , .以 为底边向上作等腰三角形 , , ,记 与 的面积的差为 ,当 的长度变化时, 始终保持不变,则 , 满足( )
A、汽车在途中加油用了10分钟 B、若 ,则加满油以后的速度为80千米/小时 C、若汽车加油后的速度是90千米/小时,则 D、该同学 到达宁波大学12. 如图,点 , , , 顺次在直线 上,以 为底边向下作等腰直角三角形 , .以 为底边向上作等腰三角形 , , ,记 与 的面积的差为 ,当 的长度变化时, 始终保持不变,则 , 满足( )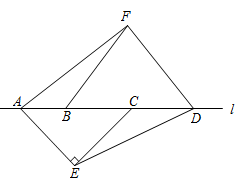 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
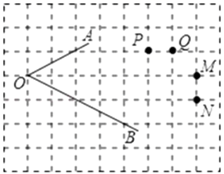
13. “两直线平行,内错角相等”的逆命题是 .14. 余姚市2020年1月1日的气温是 ,这天的最高气温是 ,最低气温是 ,则当天我市气温 的变化范围可用不等式表示为.15. 若一次函数 ( )的图象经过 和 两点,则方程 的解为.16. 在正方形网格中, 的位置如图所示,点 , , , 是四个格点,则这四个格点中到 两边距离相等的点是点.
 17. 如图,已知直线 与 轴和 轴分别交于 , 两点,点 为线段 的中点,点 在直线 上,连结 , .当 时, 的长为.
17. 如图,已知直线 与 轴和 轴分别交于 , 两点,点 为线段 的中点,点 在直线 上,连结 , .当 时, 的长为.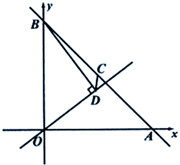 18. 如图,在 中, , , 是 边上的一个动点,点 与点 关于直线 对称,当 为直角三角形时,则 的长为.
18. 如图,在 中, , , 是 边上的一个动点,点 与点 关于直线 对称,当 为直角三角形时,则 的长为.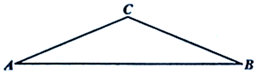
三、解答题
-
19. 解不等式组 ,并把不等式组的解集在数轴上表示出来.
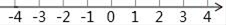 20. 作图题:如图,已知 ,线段 ,求作 ,使 . (尺规作图,不写作法,保留作图痕迹).
20. 作图题:如图,已知 ,线段 ,求作 ,使 . (尺规作图,不写作法,保留作图痕迹).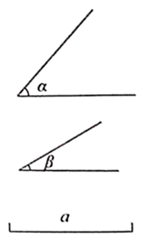 21. 如图,已知 , , ,求证: .
21. 如图,已知 , , ,求证: .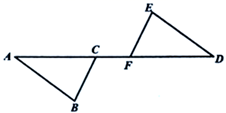 22. 如图,在直角坐标系中,长方形 的三个顶点的坐标为 , , ,且 轴,点 是长方形内一点(不含边界).
22. 如图,在直角坐标系中,长方形 的三个顶点的坐标为 , , ,且 轴,点 是长方形内一点(不含边界).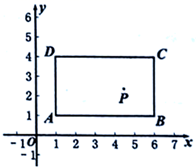 (1)、求a,b的取值范围.(2)、若将点P向左移动8个单位,再向上移动2个单位到点Q,若点Q恰好与点C关于 轴对称,求a,b的值.23. 如图, 是 的高线,且 ,E是 的中点,连结 ,取 的中点F,连结 ,求证: .
(1)、求a,b的取值范围.(2)、若将点P向左移动8个单位,再向上移动2个单位到点Q,若点Q恰好与点C关于 轴对称,求a,b的值.23. 如图, 是 的高线,且 ,E是 的中点,连结 ,取 的中点F,连结 ,求证: .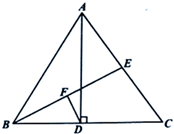 24. 宁波至绍兴城际列车已于2019年7月10日运营,这是国内首条利用既有铁路改造开行的跨市域城际铁路.其中余姚至绍兴的成人票价12元/人,学生票价6元/人.余姚某校801班师生共计50人坐城际列车去绍兴秋游.(1)、设有 名老师,求801班师生从余姚到绍兴的城际列车总费用 关于 的函数表达式.(2)、若从余姚到绍兴的城际列车总费用 不超过330元,问至少有几名学生?25. 如图,在 中, 是 的中点, 是边 上一动点,连结 ,取 的中点 ,连结 .小梦根据学习函数的经验,对 的面积与 的长度之间的关系进行了探究:
24. 宁波至绍兴城际列车已于2019年7月10日运营,这是国内首条利用既有铁路改造开行的跨市域城际铁路.其中余姚至绍兴的成人票价12元/人,学生票价6元/人.余姚某校801班师生共计50人坐城际列车去绍兴秋游.(1)、设有 名老师,求801班师生从余姚到绍兴的城际列车总费用 关于 的函数表达式.(2)、若从余姚到绍兴的城际列车总费用 不超过330元,问至少有几名学生?25. 如图,在 中, 是 的中点, 是边 上一动点,连结 ,取 的中点 ,连结 .小梦根据学习函数的经验,对 的面积与 的长度之间的关系进行了探究: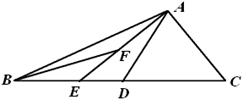 (1)、设 的长度为 , 的面积 ,通过取 边上的不同位置的点 ,经分析和计算,得到了 与 的几组值,如下表:
(1)、设 的长度为 , 的面积 ,通过取 边上的不同位置的点 ,经分析和计算,得到了 与 的几组值,如下表:0
1
2
3
4
5
6
3
1
0
2
3
根据上表可知, , .
(2)、在平面直角坐标系 中,画出(1)中所确定的函数的图象.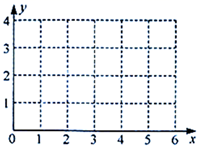 (3)、在(1)的条件下,令 的面积为 .
(3)、在(1)的条件下,令 的面积为 .①用 的代数式表示 .
②结合函数图象.解决问题:当 时, 的取值范围为.
26. 定义:两边的平方和与这两边乘积的差等于第三边平方的三角形叫做“和谐三角形”.如图1在 中,若 ,则 是“和谐三角形”.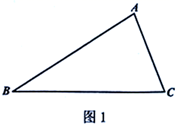 (1)、等边三角形一定是“和谐三角形”,是命题(填“真”或“假”).(2)、若 中, , , , ,且 ,若 是“和谐三角形”,求 .(3)、如图2,在等边三角形 的边 , 上各取一点 , ,且 , , 相交于点 , 是 的高,若 是“和谐三角形”,且 .
(1)、等边三角形一定是“和谐三角形”,是命题(填“真”或“假”).(2)、若 中, , , , ,且 ,若 是“和谐三角形”,求 .(3)、如图2,在等边三角形 的边 , 上各取一点 , ,且 , , 相交于点 , 是 的高,若 是“和谐三角形”,且 .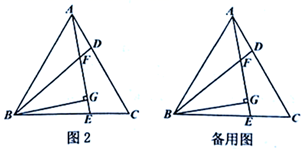
①求证: .
②连结 ,若 ,那么线段 , , 能否组成一个“和谐三角形”?若能,请给出证明:若不能,请说明理由.