浙江省台州市温岭市五校联考2019-2020学年七年级上学期数学期末考试试卷

试卷更新日期：2020-10-26 类型：期末考试

进入出卷网下载

一、选择题

1. 数轴上有A，B，C，D四个点，其中绝对值相等的点是（）

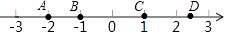A、点A与点D B、点A与点C C、点B与点C D、点B与点D

查看试题解析
2. 单项式 $- 2 x^{2} y$ 的系数和次数依次是（）

A、-2,3 B、-2,4 C、2,3 D、2,4

查看试题解析
3. 下列计算正确的是（）

A、3a+2a=5a² B、3a－a=3 C、2a³+3a²=5a⁵ D、－a²b+2a²b=a²b

查看试题解析
4. 据官方数据统计，70周年国庆阅兵网上总观看人次突破513000000，最高同时在线人数突破600万.将513000000用科学记数法表示应为（）

A、5.13×10⁸ B、5.13×10⁹ C、513×10⁶ D、0.513×10⁹

查看试题解析
5. 在下列生活、生产现象中，可以用基本事实“两点确定一条直线”来解释的是（）
①用两颗钉子就可以把木条固定在墙上；②把笔尖看成一个点，当这个点运动时便得到一条线；③把弯曲的公路改直，就能缩短路程；④植树时，只要栽下两棵树，就可以把同一行树栽在同一条直线上.

A、 $① ③$ B、 $② ④$ C、 $① ④$ D、 $② ③$

查看试题解析
6. 根据等式的性质，下列变形正确的是（）

A、如果 $2 x = 3$ ，那么 $\frac{2 x}{a} = \frac{3}{a}$ B、如果 $x = y$ ，那么 $x - 5 = 5 - y$ C、如果 $\frac{1}{2} x = 6$ ，那么 $x = 3$ D、如果 $x = y$ ，那么 $- 2 x = - 2 y$

查看试题解析
7. 从图1的正方体上截去一个三棱锥，得到一个几何体，如图2．从正面看图2的几何体，得到的平面图形是（）

A、 B、 C、 D、

查看试题解析
8. 已知∠1＝42°45′，则∠1的余角等于（）

A、47°55′ B、47°15′ C、48°15′ D、137°55′

查看试题解析
9. 正在建设的轻轨即将在2020年底验收，预计轻轨开通后，可以缩短很多人的上下班时间.小徐住在A处，每天去往B处上班，他预计乘轻轨比乘公交车上班时间将减少45分钟.已知乘轻轨从A到B处的路程比乘公交车多1千米，若轻轨行驶的平均速度为60千米/时，公交车行驶的平均速度为20千米/时，求从A到B处的乘公交车路程.若设从A到B处的乘公交车路程为x千米，则符合题意的方程是（）

A、 $\frac{x + 1}{60}$ ﹣ $\frac{x}{20}$ ＝ $\frac{3}{4}$ B、 $\frac{x}{20}$ ﹣ $\frac{x + 1}{60}$ ＝ $\frac{3}{4}$ C、 $\frac{x}{20}$ ﹣ $\frac{x + 1}{60}$ ＝45 D、 $\frac{x + 1}{60}$ ﹣ $\frac{x}{20}$ ＝45

查看试题解析
10. 找出以下图形变化的规律，计算第2019个图形中黑色正方形的个数是（）

A、3027 B、3028 C、3029 D、3030

查看试题解析

二、填空题

11. ﹣ $\sqrt{3}$ 的相反数是，倒数是．

查看试题解析
12. 如果单项式 $\frac{1}{3} x^{2 m}$ y与2x⁴yⁿ⁺³是同类项，那么n^m的值是.

查看试题解析
13. 关于x的一元一次方程 $2 x^{a - 2} + m ＝ 4$ 的解为x＝1，则a+m的值为.

查看试题解析
14. 已知代数式x﹣2y的值是5，则代数式﹣3x+6y+1的值是.

查看试题解析
15. 如图，把一张长方形的纸片沿着EF折叠，点C、D分别落在M、N的位置，且∠AEF＝ $\frac{2}{3}$ ∠DEF，则∠NEA＝.

查看试题解析
16. 如图，数轴上A、B两点之间的距离AB＝24，有一根木棒MN，MN在数轴上移动，当N移动到与A、B其中一个端点重合时，点M所对应的数为9，当N移动到线段AB的中点时，点M所对应的数为.

查看试题解析

三、解答题

17. 计算：

(1)、20﹣11+（﹣10）﹣（﹣11）

(2)、（﹣1）⁶×4+8÷（﹣ $\frac{4}{7}$ ）

查看试题解析
18. 解方程：

(1)、2x﹣9＝5x+3；

(2)、 $\frac{x - 3}{2}$ ﹣ $\frac{4 x + 1}{5}$ ＝1

查看试题解析
19. 先化简，再求值：x²﹣（2x²﹣4y）+2（x²﹣y），其中x＝﹣1，y＝ $\frac{1}{2}$ .

查看试题解析
20. 已知图中有A、B、C、D四个点，现已画出A、B、C三个点，已知D点位于A的北偏东30°方向，位于B的北偏西45°方向上.

（ 1 ）试在图中确定点D的位置；

（ 2 ）连接AB，并在AB上求作一点O，使点O到C、D两点的距离之和最小；

（ 3 ）第（2）小题画图的依据是▲.

查看试题解析
21. 如图，A、B、C三点在一条直线上，根据图形填空：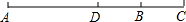

(1)、AC＝++；

(2)、AB＝AC﹣；

(3)、DB+BC＝﹣AD

(4)、若AC＝8cm，D是线段AC中点，B是线段DC中点，求线段AB的长.

查看试题解析
22. 定义一种新运算“*”满足下列条件：
①对于任意的实数a，b，a*b总有意义；

②对于任意的实数a，均有a*a＝0；

③对于任意的实数a，b，c，均有a*（b*c）＝a*b+c.

(1)、填空：1*（1*1）＝， 2*（2*2）＝， 3*0＝；

(2)、猜想a*0＝，并说明理由；

(3)、a*b＝（用含a、b的式子直接表示）.

查看试题解析

23. 平价商场经销的甲、乙两种商品，甲种商品每件售价98元，利润率为40%；乙种商品每件进价80元，售价128元.

(1)、甲种商品每件进价为元，每件乙种商品利润率为.

(2)、若该商场同时购进甲、乙两种商品共50件，恰好总进价为3800元，求购进甲、乙两种商品各多少件？

(3)、在“元且“期间，该商场只对乙种商品进行如下的优惠促销活动：按下表优惠条件，

打折前一次性购物总金额	优惠措施
少于等于480元	不优惠
超过480元，但不超过680元	其中480元不打折，超过480元的部分给予6折优惠
超过680元	按购物总额给予7.5折优惠

若小华一次性购买乙种商品实际付款576元，求小华在该商场购买乙种商品多少件？

查看试题解析

24. 如图①，已知OC是∠AOB内部的一条射线，M、N分别为OA、OB上的点，线段OM、ON同时开始旋转，线段OM以30度/秒绕点O逆时针旋转，线段ON以10度/秒的速度绕点O顺时针旋转，当OM旋转到与OB重合时，线段OM、ON都停止旋转.设OM的旋转时间为t秒.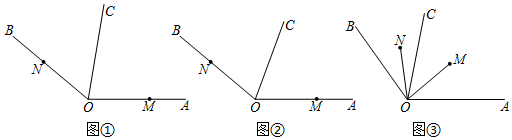

(1)、若∠AOB＝140°，当t＝2秒时，∠MON＝，当t＝4秒时，∠MON＝；

(2)、如图②，若∠AOB＝140°，OC是∠AOB的平分线，求t为何值时，两个角∠NOB与∠COM中的其中一个角是另一个角的2倍.

(3)、如图③，若OM、ON分别在∠AOC、∠COB内部旋转时，总有∠COM＝3∠CON，请直接写出 $\frac{∠ BOC}{∠ AOB}$ 的值.

查看试题解析