浙江省台州市团队六校2019-2020学年七年级上学期数学期末考试试卷

试卷更新日期：2020-10-26 类型：期末考试

进入出卷网下载

一、选择题

1. ﹣3的相反数是（）

A、 $- \frac{1}{3}$ B、 $\frac{1}{3}$ C、-3 D、3

查看试题解析
2. 2019年6月21日甬台温高速温岭联络线工程初步设计通过，本项目为沿海高速和甬台温高速公路之间的主要联络通道，总投资1289000000元，这个数据用科学记数法表示为（）

A、0.1289×10¹¹ B、1.289×10¹⁰ C、1.289×10⁹ D、1289×10⁷

查看试题解析
3. 一个由5个相同的小正方体组成的立体图形如图所示，则从正面看到的平面图形是（）

A、 B、 C、 D、

查看试题解析
4. 下列数或式： ${(- 2)}^{3}$ ， ${(- \frac{1}{3})}^{6}$ ， $- 5^{2}$ ，0， $m^{2} + 1$ 在数轴上所对应的点一定在原点右边的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
5. 有理数a，b在数轴上的对应点的位置如图所示，则下列各式成立的是（）

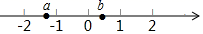A、a＞b B、﹣ab＜0 C、|a|＜|b| D、a＜﹣b

查看试题解析
6. 根据等式的性质，下列变形正确的是（）

A、若2a＝3b，则a＝ $\frac{2}{3}$ b B、若a＝b，则a+1＝b﹣1 C、若a＝b，则2﹣ $\frac{a}{3}$ ＝2﹣ $\frac{b}{3}$ D、若 $\frac{a}{2} = \frac{b}{3}$ ，则2a＝3b

查看试题解析
7. 如图，一副三角尺按不同的位置摆放，摆放位置中∠α与∠β不相等的图形是（）

A、 B、 C、 D、

查看试题解析
8. 已知a+b=7，ab=10，则代数式(5ab+4a+7b)+(3a–4ab)的值为（）

A、49 B、59 C、77 D、139

查看试题解析
9. 晚上七点刚过，小强开始做数学作业，一看钟，发现此时时针和分针在同一直线上；做完数学作业八点不到，此时时针和分针又在同一直线上，则小强做数学作业花了多少时间（）

A、30分钟 B、35分钟 C、 $\frac{420}{11}$ 分钟 D、 $\frac{360}{11}$ 分钟

查看试题解析
10. 如图，C为射线AB上一点，AB＝30，AC比BC的 $\frac{1}{4}$ 多5，P，Q两点分别从A，B两点同时出发.分别以2单位/秒和1单位/秒的速度在射线AB上沿AB方向运动，运动时间为t秒，M为BP的中点，N为QM的中点，以下结论：①BC＝2AC；②AB＝4NQ；③当PB＝ $\frac{1}{2}$ BQ时，t＝12，其中正确结论的个数是（）

A、0 B、1 C、2 D、3

查看试题解析

二、填空题

11. 多项式2x³﹣x²y²﹣1是次项式.

查看试题解析
12. 若 $- \frac{1}{2} y^{2} x^{m}$ 与5x³y²ⁿ是同类项，则m+n＝.

查看试题解析
13. 把53°24′用度表示为．

查看试题解析
14. 已知x=2是方程（a＋1）x－4a＝0的解，则a的值是 .

查看试题解析
15. 一个商店把某件商品按进价提高20%作为定价，可是总卖不出去；后来按定价减价20%出售，很快卖掉，结果这次生意亏了4元.那么这件商品的进价是元.

查看试题解析
16. 如图，将一张长方形纸片分別沿着EP，FP对折，使点B落在点B，点C落在点C′.若点P，B′，C′不在一条直线上，且两条折痕的夹角∠EPF＝85°，则∠B′PC′＝.

查看试题解析
17. 已知a，m，n均为有理数，且满足 $| a - m | = 5, | n - a | = 3$ ，那么 $| m - n |$ 的值为 .

查看试题解析
18. 定义一种对正整数n的“C运算”：①当n为奇数时，结果为3n+1；②当n为偶数时，结果为 $\frac{n}{2^{k}}$ （其中k是使 $\frac{n}{2^{k}}$ 为奇数的正整数）并且运算重复进行，例如，n＝66时，其“C运算”如下：

若n＝26，则第2019次“C运算”的结果是.

查看试题解析

三、解答题

19. 计算：﹣6÷2+ $(\frac{1}{3} - \frac{1}{4})$ ×12+（﹣3）² .

查看试题解析
20. 解方程 $\frac{3 x - 1}{2} = \frac{4 x + 2}{5} - 1$ .

查看试题解析
21. 先化简后求值：2（x²y+xy）﹣3（x²y﹣xy）﹣5xy，其中x＝﹣2，y＝1.

查看试题解析
22. 已知：如图，平面上有A、B、C、D、F五个点，根据下列语句画出图形：

（Ⅰ）直线BC与射线AD相交于点M；

（Ⅱ）连接AB，并反向延长线段AB至点E，使AE= $\frac{1}{2}$ BE；

（Ⅲ）①在直线BC上求作一点P，使点P到A、F两点的距离之和最小；

②作图的依据是▲.

查看试题解析
23. 如图所示，OE和OD分别是∠AOB和∠BOC的平分线，且∠AOB＝90°，∠EOD＝67.5°的度数.

(1)、求∠BOD的度数；

(2)、∠AOE与∠BOC互余吗？请说明理由.

查看试题解析
24. 如图，图1中小正方形的个数为1个；图2中小正方形的个数为：1+3＝4＝2²个；图3中小正方形的个数为：1+3+5＝9＝3²个；图4中小正方形的个数为：1+3+5+7＝16＝4²个；…

(1)、根据你的发现，第n个图形中有小正方形：1+3+5+7+…+＝个.

(2)、由（1）的结论，解答下列问题：已知连续奇数的和：（2n+1）+（2n+3）+（2n+5）+……+137+139＝3300，求n的值.

查看试题解析
25. 微信运动和腾讯公益推出了一个爱心公益活动：一天中走路步数达到10000步及以上可通过微信运动和腾讯基金会向公益活动捐款，如果步数在10000步及以上，每步可捐0.0002元；若步数在10000步以下，则不能参与捐款．

(1)、老赵某天的步数为13000步，则他当日可捐多少钱？

(2)、已知甲、乙、丙三人某天通过步数共捐了8.4元，且甲的步数=乙的步数=丙步数的3倍，则丙走了多少步
？

查看试题解析
26. 数学问题：计算 $\frac{1}{m} + \frac{1}{m^{2}} + \frac{1}{m^{3}} + \dots + \frac{1}{m^{n}}$ （其中m，n都是正整数，且m≥2，n≥1）.
探究问题：为解决上面的数学问题，我们运用数形结合的思想方法，通过不断地分割一个面积为1的正方形，把数量关系和几何图形巧妙地结合起来，并采取一般问题特殊化的策略来进行探究.

探究一：计算 $\frac{1}{2} + \frac{1}{2^{2}} + \frac{1}{2^{3}} + \dots + \frac{1}{2^{n}}$ .

第1次分割，把正方形的面积二等分，其中阴影部分的面积为 $\frac{1}{2}$ ；

第2次分割，把上次分割图中空白部分的面积继续二等分，阴影部分的面积之和为 $\frac{1}{2}$ + $\frac{1}{2^{2}}$ ；

第3次分割，把上次分割图中空白部分的面积继续二等分，…；

…

第n次分割，把上次分割图中空白部分的面积最后二等分，所有阴影部分的面积之和为 $\frac{1}{2}$ + $\frac{1}{2^{2}}$ + $\frac{1}{2^{3}}$ +…+ $\frac{1}{2^{n}}$ ，最后空白部分的面积是 $\frac{1}{2^{n}}$ .

根据第n次分割图可得等式： $\frac{1}{2}$ + $\frac{1}{2^{2}}$ + $\frac{1}{2^{3}}$ +…+ $\frac{1}{2^{n}}$ =1﹣ $\frac{1}{2^{n}}$ .

探究二：计算 $\frac{1}{3}$ + $\frac{1}{3^{2}}$ + $\frac{1}{3^{3}}$ +…+ $\frac{1}{3^{n}}$ .

第1次分割，把正方形的面积三等分，其中阴影部分的面积为 $\frac{2}{3}$ ；

第2次分割，把上次分割图中空白部分的面积继续三等分，阴影部分的面积之和为 $\frac{2}{3}$ + $\frac{2}{3^{2}}$ ；

第3次分割，把上次分割图中空白部分的面积继续三等分，…；

…

第n次分割，把上次分割图中空白部分的面积最后三等分，所有阴影部分的面积之和为 $\frac{2}{3}$ + $\frac{2}{3^{2}}$ + $\frac{2}{3^{3}}$ +…+ $\frac{2}{3^{n}}$ ，最后空白部分的面积是 $\frac{1}{3^{n}}$ .

根据第n次分割图可得等式： $\frac{2}{3}$ + $\frac{2}{3^{2}}$ + $\frac{2}{3^{3}}$ +…+ $\frac{2}{3^{n}}$ =1﹣ $\frac{1}{3^{n}}$ ，

两边同除以2，得 $\frac{1}{3}$ + $\frac{1}{3^{2}}$ + $\frac{1}{3^{3}}$ +…+ $\frac{1}{3^{n}}$ = $\frac{1}{2}$ ﹣ $\frac{1}{2 \times 3^{n}}$ .

探究三：

(1)、计算 $\frac{1}{4}$ + $\frac{1}{4^{2}}$ + $\frac{1}{4^{3}}$ +…+ $\frac{1}{4^{n}}$ .

(2)、（仿照上述方法，只画出第n次分割图，在图上标注阴影部分面积，并写出探究过程）

解决问题：计算 $\frac{1}{m}$ + $\frac{1}{m^{2}}$ + $\frac{1}{m^{3}}$ +…+ $\frac{1}{m^{n}}$ .

（只需画出第n次分割图，在图上标注阴影部分面积，并完成以下填空）

根据第n次分割图可得等式：，

所以， $\frac{1}{m}$ + $\frac{1}{m^{2}}$ + $\frac{1}{m^{3}}$ +…+ $\frac{1}{m^{n}}$ =.

(3)、拓广应用：计算 $\frac{5 - 1}{5}$ + $\frac{5^{2} - 1}{5^{2}}$ + $\frac{5^{3} - 1}{5^{3}}$ +…+ $\frac{5^{n} - 1}{5^{n}}$ .

查看试题解析