重庆市云阳县“互帮互学”联盟2020届九年级上学期数学期中考试试卷
试卷更新日期:2020-10-26 类型:期中考试
一、选择题
-
1. 下列图案中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 点P(3,2)关于原点对称的点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 抛物线y=(x﹣2)2﹣3的顶点坐标是( )A、(2,﹣3) B、(﹣2,3) C、(2,3) D、(﹣2,﹣3)4. 一元二次方程x2+2x+2=0的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根5. 用配方法解一元二次方程x2﹣4x﹣1=0,配方后得到的方程是( )A、(x﹣2)2=1 B、(x﹣2)2=4 C、(x﹣2)2=5 D、(x﹣2)2=36. 将二次函数y=x2的图象向右平移1个单位,再向上平移2个单位后,所得图象的函数表达式是( )A、y=(x-1)2+2 B、y=(x+1)2+2 C、y=(x-1)2-2 D、y=(x+1)2-27. 为了美化环境,某市加大绿化投资,2015年用于绿化投资300万元,2017年用于绿化投资1040万元,求这两年绿化投资的年均增长率.设这两年绿化投资年平均增长率为x,所列方程为A、 B、 C、 D、8. 估计 的值应在( )A、3和4之间 B、4和5之间 C、5和6之间 D、6和7之间9. 如图,下列图形都是由同样大小的小黑点按一定规律所组成的.图①中共有2个小黑点,图②中共有7个小黑点,…,按此规律,则图⑦中小黑点的个数是( )
2. 点P(3,2)关于原点对称的点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 抛物线y=(x﹣2)2﹣3的顶点坐标是( )A、(2,﹣3) B、(﹣2,3) C、(2,3) D、(﹣2,﹣3)4. 一元二次方程x2+2x+2=0的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根5. 用配方法解一元二次方程x2﹣4x﹣1=0,配方后得到的方程是( )A、(x﹣2)2=1 B、(x﹣2)2=4 C、(x﹣2)2=5 D、(x﹣2)2=36. 将二次函数y=x2的图象向右平移1个单位,再向上平移2个单位后,所得图象的函数表达式是( )A、y=(x-1)2+2 B、y=(x+1)2+2 C、y=(x-1)2-2 D、y=(x+1)2-27. 为了美化环境,某市加大绿化投资,2015年用于绿化投资300万元,2017年用于绿化投资1040万元,求这两年绿化投资的年均增长率.设这两年绿化投资年平均增长率为x,所列方程为A、 B、 C、 D、8. 估计 的值应在( )A、3和4之间 B、4和5之间 C、5和6之间 D、6和7之间9. 如图,下列图形都是由同样大小的小黑点按一定规律所组成的.图①中共有2个小黑点,图②中共有7个小黑点,…,按此规律,则图⑦中小黑点的个数是( ) A、48 B、62 C、63 D、7910. 已知m,n是方程 的两个根,则代数式 的值等于( )A、 B、3 C、5 D、11. 函数y=ax2﹣2x+1和y=ax+a(a是常数,且a≠0)在同一直角坐标系中的图象可能是( )A、
A、48 B、62 C、63 D、7910. 已知m,n是方程 的两个根,则代数式 的值等于( )A、 B、3 C、5 D、11. 函数y=ax2﹣2x+1和y=ax+a(a是常数,且a≠0)在同一直角坐标系中的图象可能是( )A、 B、
B、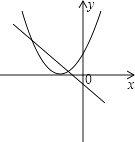 C、
C、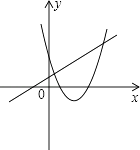 D、
D、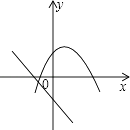 12. 若数m使关于x的不等式组 有解且至多有3个整数解,且使关于y的分式方程 的解满足-3≤y≤4,则满足条件的所有整数m的个数是( )A、6 B、5 C、4 D、3
12. 若数m使关于x的不等式组 有解且至多有3个整数解,且使关于y的分式方程 的解满足-3≤y≤4,则满足条件的所有整数m的个数是( )A、6 B、5 C、4 D、3二、填空题
-
13. 已知x=2是一元二次方程x2﹣2mx+4=0的一个解,则m的值为14. 如图是抛物线y=ax2+bx+c的图象的一部分,请你根据图象写出方程ax2+bx+c=0的两根是 .
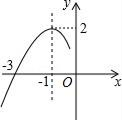 15. 如图,将等腰直角三角形 绕点 逆时针旋转15度得到 ,若 ,则阴影部分的面积为.
15. 如图,将等腰直角三角形 绕点 逆时针旋转15度得到 ,若 ,则阴影部分的面积为. 16. 某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销,据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本,当销售单价是元时,每天获利最多.17. 在一条笔直的公路上顺次有A、B、C三地,甲车从B地出发往A地匀速行驶,到达A地后停止.在甲车出发的同时,乙车也从B地出发往A地匀速行驶,到达A地停留1小时后,调头按原速向C地行驶.若AB两地相距300千米,在两车行驶的过程中,甲、乙两车之间的距离y(千米)与乙车行驶时间x(小时)之间的函数图象如图所示,则在两车出发后经过小时相遇.
16. 某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销,据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本,当销售单价是元时,每天获利最多.17. 在一条笔直的公路上顺次有A、B、C三地,甲车从B地出发往A地匀速行驶,到达A地后停止.在甲车出发的同时,乙车也从B地出发往A地匀速行驶,到达A地停留1小时后,调头按原速向C地行驶.若AB两地相距300千米,在两车行驶的过程中,甲、乙两车之间的距离y(千米)与乙车行驶时间x(小时)之间的函数图象如图所示,则在两车出发后经过小时相遇. 18. 初2019级即将迎来中考,很多家长都在为孩子准备营养午餐.一家快餐店看准了商机,在5月5号推出了A,B,C三种营养套餐.套餐C单价比套餐A贵5元,三种套餐的单价均为整数,其中A套餐比C套餐少卖12份,B套餐比C套餐少卖6份,且C套餐当天卖出的数量大于26且不超过32,当天总销售量为偶数且当天销售额达到了1830元,商家发现C套餐很受欢迎,因此在6号加推出了C套餐升级版D套餐,四种套餐同时售卖,A套餐比5号销售量减少,C套餐比5号销售量增加 ,且A减少的份数比C套餐增加的份数多5份,B套餐销售量不变,由于商家人手限制,两天的总销售量相同,则其他套餐单价不变的情况下,D套餐至少比C套餐费贵时,才能使6号销售额达到1950元.
18. 初2019级即将迎来中考,很多家长都在为孩子准备营养午餐.一家快餐店看准了商机,在5月5号推出了A,B,C三种营养套餐.套餐C单价比套餐A贵5元,三种套餐的单价均为整数,其中A套餐比C套餐少卖12份,B套餐比C套餐少卖6份,且C套餐当天卖出的数量大于26且不超过32,当天总销售量为偶数且当天销售额达到了1830元,商家发现C套餐很受欢迎,因此在6号加推出了C套餐升级版D套餐,四种套餐同时售卖,A套餐比5号销售量减少,C套餐比5号销售量增加 ,且A减少的份数比C套餐增加的份数多5份,B套餐销售量不变,由于商家人手限制,两天的总销售量相同,则其他套餐单价不变的情况下,D套餐至少比C套餐费贵时,才能使6号销售额达到1950元.三、解答题
-
19. 解一元二次方程:(1)、(2)、20. 如图,已知 的三个顶点坐标为 , , .

( 1 )将 绕坐标原点O旋转 ,画出旋转后的 ,并写出点A的对应点 的坐标;
( 2 )将 绕坐标原点O逆时针旋转 ,直接写出点A的对应点Q的坐标 ▲ ;
( 3 )请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标 ▲ .
21. 先化简,再求值: ,其中x是方程 的根.22. 如图,在平面直角坐标系中,抛物线 经过点 , ,点P是直线 上的动点,过点P作x轴的垂线交抛物线于点M,设点P的横坐标为t. (1)、分别求出直线 和这条抛物线的解析式.(2)、若点P在第四象限,连接 、 ,当线段 最长时,求 的面积.23. 暑假是旅游旺季,为吸引游客,某旅游公司推出两条“精品路线”——“亲子游”和“夏令营”.(1)7月份,“亲子游”和“夏令营”活动的价格分别为8000元/人和12000元/人.其中,参加“夏令营”活动的游客人数为“亲子游”活动游客人数的2倍少300人,且“夏令营”线路的旅游总收入不低于“亲子游”线路旅游总收入的一半,
(1)、分别求出直线 和这条抛物线的解析式.(2)、若点P在第四象限,连接 、 ,当线段 最长时,求 的面积.23. 暑假是旅游旺季,为吸引游客,某旅游公司推出两条“精品路线”——“亲子游”和“夏令营”.(1)7月份,“亲子游”和“夏令营”活动的价格分别为8000元/人和12000元/人.其中,参加“夏令营”活动的游客人数为“亲子游”活动游客人数的2倍少300人,且“夏令营”线路的旅游总收入不低于“亲子游”线路旅游总收入的一半,问:
(1)、参加“亲子游”线路的旅游人数至少有多少人?(2)、到了8月份,该旅游公司实行降价促销活动,“亲子游”和“夏令营”线路的价格分别下降 和 (a<20),旅游人数在7月份对应最小值的基础上分别上升 和 ,当月旅游总收入达到256.32万元,求a24. 材料阅读:类比是数学中常用的数学思想.比如,我们可以类比多位数的加、减、乘、除的竖式运算方法,得到多项式与多项式的加、减、乘、除的运算方法.

理解应用:
(1)、请仿照上面的竖式方法计算: ;(2)、已知两个多项式的和为 ,其中一个多项式为 .请用竖式的方法求出另一个多项式.(3)、已知一个长为 ,宽为 的矩形A,将它的长增加8.宽增加a得到一个新矩形B,且矩形B的周长是A周长的3倍(如图).同时,矩形B的面积和另一个一边长为 的矩形C的面积相等,求m的值和矩形C的另一边长. 25. 如图1,在▱ABCD中,∠D=45°,E为BC上一点,连接AC,AE,
25. 如图1,在▱ABCD中,∠D=45°,E为BC上一点,连接AC,AE, (1)、若AB=2 ,AE=4,求BE的长;(2)、如图2,过C作CM⊥AD于M,F为AE上一点,CA=CF,且∠ACF=∠BAE,求证:AF+AB= AM.26. 如图1,抛物线 与 轴相交于A、B两点(点A在点B的右侧),与 轴相交于点C,对称轴与 轴相交于点H,与 相交于点T.
(1)、若AB=2 ,AE=4,求BE的长;(2)、如图2,过C作CM⊥AD于M,F为AE上一点,CA=CF,且∠ACF=∠BAE,求证:AF+AB= AM.26. 如图1,抛物线 与 轴相交于A、B两点(点A在点B的右侧),与 轴相交于点C,对称轴与 轴相交于点H,与 相交于点T. (1)、点P是线段 上方抛物线上一点,过点P作 交抛物线的对称轴于点Q,当 面积最大时,点M、N在y轴上(点M在点N的上方), ,点G在直线 上,求 的最小值.(2)、点E为 中点, 轴于F,连接 ,将 沿 翻折得△ ,如图所示,再将△ 沿直线 平移,记平移中的△ 为△ ,在平移过程中,直线 与x轴交于点R,则是否存在这样的点R,使得△ 为等腰三角形?若存在,求出R点坐标.
(1)、点P是线段 上方抛物线上一点,过点P作 交抛物线的对称轴于点Q,当 面积最大时,点M、N在y轴上(点M在点N的上方), ,点G在直线 上,求 的最小值.(2)、点E为 中点, 轴于F,连接 ,将 沿 翻折得△ ,如图所示,再将△ 沿直线 平移,记平移中的△ 为△ ,在平移过程中,直线 与x轴交于点R,则是否存在这样的点R,使得△ 为等腰三角形?若存在,求出R点坐标.