重庆市江津区六校联考2020届九年级上学期数学期中考试试卷
试卷更新日期:2020-10-26 类型:期中考试
一、选择题
-
1. 下列方程中,是关于x的一元二次方程的是( )A、3x2+2x+y=0 B、4x2+ ﹣2=0 C、(x+1)2=x2+1 D、x2﹣2x+1=﹣x2. 一元二次方程2x2﹣6x+3=0根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、有两个实数根3. 抛物线 的顶点坐标是( )A、(﹣1,2) B、(﹣1,﹣2) C、(1,﹣2) D、(1,2)4. 将抛物线y=2x2向上平移2个单位,再向右平移3个单位,所得抛物线的解析式为( )A、y=2(x﹣3)2+2 B、y=2(x+3)2+2 C、y=2(x+3)2﹣2 D、y=2(x﹣3)2﹣25. 用配方法解一元二次方程x2﹣6x﹣2=0,配方后得到的方程是( )A、(x﹣3)2=2 B、(x﹣3)2=8 C、(x﹣3)2=11 D、(x+3)2=96. 已知一元二次方程x2﹣6x+8=0的两个解恰好分别是等腰△ABC的底和腰,则△ABC的周长为( )A、10 B、10或8 C、9 D、87. 某种品牌运动服经过两次降价,每件零售价由560元降为315元,已知两次降价的百分率相同,求每次降价的百分率.设每次降价的百分率为x,下面所列的方程中正确的是( )
A、560(1+x)2=315 B、560(1-x)2=315 C、560(1-2x)2=315 D、560(1-x2)=3158. 已知a、b为实数,且满足(a2+b2)2﹣9=0,则a2+b2的值为( )A、±3 B、3 C、±9 D、99. 二次函数y=ax2+bx的图象如图所示,那么一次函数y=ax+b的图象大致是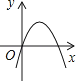 A、
A、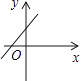 B、
B、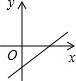 C、
C、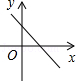 D、
D、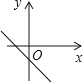 10. 从正方形的铁皮上,截去2cm宽的一条长方形,余下的面积是48cm2 , 则原来的正方形铁皮的边长是( )A、7cm B、8cm C、9cm D、10cm11. 如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴是直线x=﹣2.关于下列结论:①ab<0;②b2﹣4ac>0;③9a﹣3b+c<0;④b﹣4a=0;⑤方程ax2+bx=0的两个根为x1=0,x2=﹣4,其中正确的结论有( )
10. 从正方形的铁皮上,截去2cm宽的一条长方形,余下的面积是48cm2 , 则原来的正方形铁皮的边长是( )A、7cm B、8cm C、9cm D、10cm11. 如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴是直线x=﹣2.关于下列结论:①ab<0;②b2﹣4ac>0;③9a﹣3b+c<0;④b﹣4a=0;⑤方程ax2+bx=0的两个根为x1=0,x2=﹣4,其中正确的结论有( )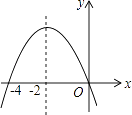 A、①③④ B、②④⑤ C、①②⑤ D、②③⑤12. 已知抛物线y=ax2+3x+4与x轴有两个交点,且关于x的不等式组 的解集为x<﹣2,那么符合条件的所有整数a有多少个( )A、1个 B、2个 C、3个 D、4个
A、①③④ B、②④⑤ C、①②⑤ D、②③⑤12. 已知抛物线y=ax2+3x+4与x轴有两个交点,且关于x的不等式组 的解集为x<﹣2,那么符合条件的所有整数a有多少个( )A、1个 B、2个 C、3个 D、4个二、填空题
-
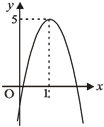
13. 一元二次方程(x﹣1)2=0的根是.14. 抛物线y=x2﹣4x+3的对称轴是直线.15. 某种植物的主干长出若干数目的枝干,每个枝干又长出相同数目的小分支,若小分支、枝干和主干的总数是73,则每个枝干长出个小分支.16. 已知二次函数 的图象如图所示,若方程 有两个不相等的实数根,则 的取值范围是。
 17. 如图,A、B、C、D为矩形的四个顶点,AB=16cm,AD=8cm,动点P,Q分别从点A、C同时出发,点P以3cm/S的速度向B移动,一直到达B为止;点Q以2cm/s的速度向D移动.当P、Q两点从出发开始到秒时,点P和点Q的距离是10cm.
17. 如图,A、B、C、D为矩形的四个顶点,AB=16cm,AD=8cm,动点P,Q分别从点A、C同时出发,点P以3cm/S的速度向B移动,一直到达B为止;点Q以2cm/s的速度向D移动.当P、Q两点从出发开始到秒时,点P和点Q的距离是10cm. 18. 如图,在平面直角坐标系中,过点P(m,0)作x轴的垂线,分别交抛物线y= x2+2与直线y=﹣ x于A、B,以线段AB为对角线作正方形ACBD,则正方形ACBD的面积的最小值为.
18. 如图,在平面直角坐标系中,过点P(m,0)作x轴的垂线,分别交抛物线y= x2+2与直线y=﹣ x于A、B,以线段AB为对角线作正方形ACBD,则正方形ACBD的面积的最小值为.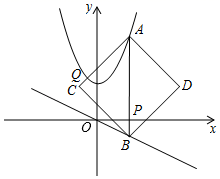
三、解答题
-
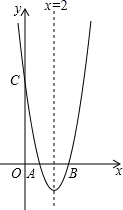
19. 解下列方程:(1)、x2=3x;(2)、x2+2x﹣4=0.20. 如图,已知二次函数的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,6),对称轴为直线x=2,顶点为D.求二次函数的解析式及四边形ADBC的面积.
 21. 先化简,再求值:( ﹣ )÷ ,其中x是方程2x2﹣7x+3=0的解.22. 某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米.
21. 先化简,再求值:( ﹣ )÷ ,其中x是方程2x2﹣7x+3=0的解.22. 某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米.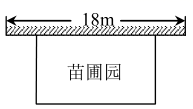 (1)、若苗圃园的面积为72平方米,求x;(2)、若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由;23. 小慧同学根据学习函数的经验,对函数y=|x﹣1|的图象与性质进行了探究.下面是小慧的探究过程,请补充完成:(1)、函数y=|x﹣1|的自变量x的取值范围是.(2)、列表,找出y与x的几组对应值.
(1)、若苗圃园的面积为72平方米,求x;(2)、若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由;23. 小慧同学根据学习函数的经验,对函数y=|x﹣1|的图象与性质进行了探究.下面是小慧的探究过程,请补充完成:(1)、函数y=|x﹣1|的自变量x的取值范围是.(2)、列表,找出y与x的几组对应值.x
…
﹣1
0
1
2
3
…
y
…
2
b
0
1
2
…
其中,b=.
(3)、在所给的平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点,并画出该函数的图象; (4)、请根据你画出的函数图象,完成:当x=﹣5时.y=.当2012≤|y|≤2019时,x的取值范围是.24. 某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
(4)、请根据你画出的函数图象,完成:当x=﹣5时.y=.当2012≤|y|≤2019时,x的取值范围是.24. 某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:售价x(元/千克)
50
60
70
销售量y(千克)
100
80
60
(1)、求y与x之间的函数表达式;
(2)、设商品每天的总利润为W(元),则当售价x定为多少元时,厂商每天能获得最大利润?最大利润是多少?(3)、如果超市要获得每天不低于1350元的利润,且符合超市自己的规定,那么该商品每千克售价的取值范围是多少?请说明理由.25. 今年国庆期间解放碑、洪崖洞、朝天门、来福士、长嘉汇等景点人员密集;穿楼而过的轻轨、洪崖洞、灯光秀……吸引着海量游客前来重庆打卡.位于洪崖洞的重庆知名火锅小天鹅火锅在节日期间每天也人满为患,其中鸳鸯火锅和红汤火锅最受游客青睐.在中秋节期间,前来就餐选择鸳鸯火锅和红汤火锅的游客共有2000名,鸳鸯火锅和红汤火锅的人均消费分别为180元和120元.(1)、中秋节期间,若选择红汤火锅的人数不超过鸳鸯火锅人数的1.5倍.求至少有多少人选择鸳鸯火锅?(2)、“国庆”节期间,前来就餐的游客人数有所下降,与(1)问中选择鸳鸯火锅的人数最少时相比,选择两种火锅的人数均下降了a%;人均消费与中秋节期间相比均有所上升,其中鸳鸯火锅的人均消费上涨了a%,红汤火锅的人均消费上涨了 a%,最终“国庆”节期间两种火锅的总销售额与(1)问中选择鸳鸯火锅的人数最少时的两种火锅的总销售额持平,求a的值.26. 如图1,已知抛物线y=﹣x2+2x+c与x轴交于A、B两点,其中点A(﹣1,0),抛物线与y轴交于点C,顶点为D.
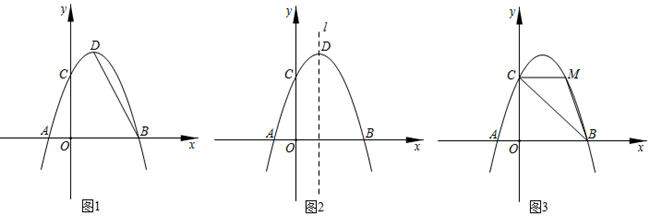 (1)、如图2,直线l是抛物线的对称轴,点P是直线l上一动点,是否存在点P,使△PBC是直角三角形?若存在,求点P的坐标;若不存在,说明理由.(2)、如图3,连接BC,点M是直线BC上方的抛物线上的一个动点,当△MBC的面积最大时,求△MBC的面积的最大值;点N是线段BC上的一点,求MN+ BN的最小值.
(1)、如图2,直线l是抛物线的对称轴,点P是直线l上一动点,是否存在点P,使△PBC是直角三角形?若存在,求点P的坐标;若不存在,说明理由.(2)、如图3,连接BC,点M是直线BC上方的抛物线上的一个动点,当△MBC的面积最大时,求△MBC的面积的最大值;点N是线段BC上的一点,求MN+ BN的最小值.