浙江省宁波市2021届九年级上学期数学第一次月考试卷
试卷更新日期:2020-10-26 类型:月考试卷
一、选择题(每小题4分,共40分,在每小题给出的四个选项中,只有一个符合题目要求)
-
1. 二次函数y=(x-1)2+3图象的顶点坐标是( )A、(-1,3) B、(1,-3) C、(-1,-3) D、(1,3)2. “ 是实数, ”这一事件是( )A、 必然事件 B、不确定事件 C、不可能事件 D、 随机事件3. 小亮、小莹、大刚三位同学随机站成一排合影留念,小亮恰好站在中间的概率是( )A、 B、 C、 D、4. 下列有关圆的一些结论:①任意三点确定一个圆;②相等的圆心角所对的弧相等;③平分弦的直径垂直于弦,并且平分弦所对的弧,④三角形的外心到三角形各顶点的距离相等.其中错误的结论有( )A、1个 B、2个 C、3个 D、4个5. 如图,在等边三角形ABC中,AB、AC都是⊙O的弦,OM⊥AB , ON⊥AC , 垂足分别为点M , N.如果MN=1,那么BC等于( )
 A、1 B、2 C、3 D、46. 如图,二次函数y=ax2+bx的图象开口向下,且经过第三象限的点P.若点P的横坐标为-1,则一次函数y=(a-b)x+b的图象大致是( )
A、1 B、2 C、3 D、46. 如图,二次函数y=ax2+bx的图象开口向下,且经过第三象限的点P.若点P的横坐标为-1,则一次函数y=(a-b)x+b的图象大致是( )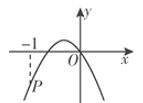 A、
A、 B、
B、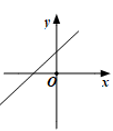 C、
C、 D、
D、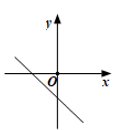 7. 如图,在⊙O中,如果 , 那么( )
7. 如图,在⊙O中,如果 , 那么( )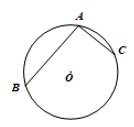 A、AB=AC B、AB=2AC C、AB<2AC D、AB>2AC8. 如图,二次函数y=ax2+bx+c的图象与x轴交于点A(-1,0),对称轴为直线x=2.与y轴的交点B在(0,2)与(0,3)之间(不包括这两点),下列结论:①abc<0;②5a+c>0;③若点M( ,y1 ),点N( ,y2)是函数图象上的两点,则y1<y2;④ < a < .其中正确结论有( )
A、AB=AC B、AB=2AC C、AB<2AC D、AB>2AC8. 如图,二次函数y=ax2+bx+c的图象与x轴交于点A(-1,0),对称轴为直线x=2.与y轴的交点B在(0,2)与(0,3)之间(不包括这两点),下列结论:①abc<0;②5a+c>0;③若点M( ,y1 ),点N( ,y2)是函数图象上的两点,则y1<y2;④ < a < .其中正确结论有( )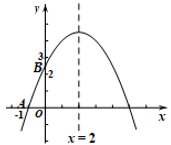 A、1个 B、2个 C、3个 D、4个9. 抛物线y=x2+bx+3的对称轴为直线x=1.若关于x的一元二次方程x2+bx+3-t=0(t为实数)在-1<x<4的范围内有实数根,则t的取值范围是( )A、2 ≤ t<11 B、t ≥2 C、6<t<11 D、2 ≤ t<610. 已知抛物线 过A(m , 3),B(n , 3)两点,若线段AB的长不大于4,则代数式 的最小值是( )A、 B、 C、 D、
A、1个 B、2个 C、3个 D、4个9. 抛物线y=x2+bx+3的对称轴为直线x=1.若关于x的一元二次方程x2+bx+3-t=0(t为实数)在-1<x<4的范围内有实数根,则t的取值范围是( )A、2 ≤ t<11 B、t ≥2 C、6<t<11 D、2 ≤ t<610. 已知抛物线 过A(m , 3),B(n , 3)两点,若线段AB的长不大于4,则代数式 的最小值是( )A、 B、 C、 D、二、填空题(本题有6小题,每小题5分,共30分)
-
11. 有5张看上去无差别的卡片,上面分别写着1,2,3,4,5.随机抽取1张,抽出的数字是2的倍数的概率是 .12. 我国古代数学经典著作《九章算术》中记载了一个“圆材埋壁”的问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?”意思是:今有一圆柱形木材,埋在墙壁中,不知其大小.用锯去锯这木材,锯口深ED=1寸,锯道长AB=1尺(1尺=10寸).问这根圆形木材的直径是寸.
 13. AB是⊙O的弦, ,垂足为M , 连结OA . 若 中有一个角是 , ,则弦AB的长为 .
13. AB是⊙O的弦, ,垂足为M , 连结OA . 若 中有一个角是 , ,则弦AB的长为 .
14. 如图1,是一款优雅且稳定的抛物线型落地灯. 防滑螺母C为抛物线支架的最高点,灯罩D距离地面1.86米,灯柱AB及支架的相关数据如图2所示. 若茶几摆放在灯罩的正下方,则茶几到灯柱的距离AE为米. 15. 已知关于x的函数 ,当0≤x≤3时函数有最大值5,则a= .16. 如图,已知抛物线 与x轴交于A , B两点,对称轴与抛物线交于点C , 与x轴交于点D , ⊙C的半径为2,G为⊙C上一动点,P为AG的中点,则线段DP长的最大值为.
15. 已知关于x的函数 ,当0≤x≤3时函数有最大值5,则a= .16. 如图,已知抛物线 与x轴交于A , B两点,对称轴与抛物线交于点C , 与x轴交于点D , ⊙C的半径为2,G为⊙C上一动点,P为AG的中点,则线段DP长的最大值为.
三、解答题(本大题共8小题,共80分)
-
17. 如图,在10×10的正方形网格中(每个小正方形的边长都为1个单位),△ABC的三个顶点都在格点上.建立如图所示的直角坐标系,

( 1 )请在图中标出△ABC的外接圆的圆心P的位置;并填写:圆心P的坐标:P(▲ , ▲);
( 2 )将△ABC绕点A逆时针旋转90°得到△ADE , 画出△ADE .
18. 现有小莉,小罗,小强三个自愿献血者,两人血型为O型,一人血型为A型.若在三人中随意挑选一人献血,两年以后又从此三人中随意挑选一人献血,试求两次所抽血的血型均为O型的概率.(要求:用列表或画树状图的方法解答)19. 如图,AB是半圆的直径,O是圆心,C是半圆上一点,D是弧AC中点,OD交弦AC于E , 连结BE , 若AC=8,DE=2,求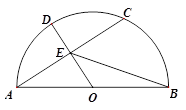 (1)、求半圆的半径长;(2)、BE的长度.20. 如图,二次函数的图象与x轴交于A(-3,0)和B(1,0)两点,交y轴于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D .
(1)、求半圆的半径长;(2)、BE的长度.20. 如图,二次函数的图象与x轴交于A(-3,0)和B(1,0)两点,交y轴于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D .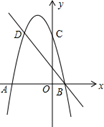 (1)、请直接写出D点的坐标;(2)、求一次函数和二次函数的解析式;(3)、根据图象直接写出使一次函数值大于二次函数值的x的取值范围.21. 2020年8月,今年第4号台风“黑格比”来袭,宁波市某镇被雨水“围攻”,如图,当地有一拱桥为圆弧形,跨度AB=24米,拱高PM=8米,当洪水泛滥,水面跨度缩小到8米时要采取紧急措施,当时测量人员测得水面A1B1到拱顶距离只有1米,问是否需要采取紧急措施?请说明理由.
(1)、请直接写出D点的坐标;(2)、求一次函数和二次函数的解析式;(3)、根据图象直接写出使一次函数值大于二次函数值的x的取值范围.21. 2020年8月,今年第4号台风“黑格比”来袭,宁波市某镇被雨水“围攻”,如图,当地有一拱桥为圆弧形,跨度AB=24米,拱高PM=8米,当洪水泛滥,水面跨度缩小到8米时要采取紧急措施,当时测量人员测得水面A1B1到拱顶距离只有1米,问是否需要采取紧急措施?请说明理由. 22. 某商店原来平均每天可销售某种水果200kg , 每千克可盈利6元,为减少库存,经市场调查,如果这种水果每千克降价1元,则每天可多售出20kg.(1)、设每千克水果降价x元,平均每天盈利y元,试写出y关于x的函数表达式.(2)、若要平均每天盈利960元,则每千克应降价多少元?(3)、商店为了尽快减少库存且让利于顾客,决定对该批水果每千克至少降价3元,试问该批水果每千克应降价多少元才能达到最大利润,并求出最大利润?23. 在平面直角坐标系 xOy 中,点 P 的坐标为 (a,b) ,当a>b 时,点P' 的坐标为 (-a,b);当 a≤b 时,点P' 的坐标为 (-b,a) ,这样的点 P' 叫做点 P 的“中和点”.
22. 某商店原来平均每天可销售某种水果200kg , 每千克可盈利6元,为减少库存,经市场调查,如果这种水果每千克降价1元,则每天可多售出20kg.(1)、设每千克水果降价x元,平均每天盈利y元,试写出y关于x的函数表达式.(2)、若要平均每天盈利960元,则每千克应降价多少元?(3)、商店为了尽快减少库存且让利于顾客,决定对该批水果每千克至少降价3元,试问该批水果每千克应降价多少元才能达到最大利润,并求出最大利润?23. 在平面直角坐标系 xOy 中,点 P 的坐标为 (a,b) ,当a>b 时,点P' 的坐标为 (-a,b);当 a≤b 时,点P' 的坐标为 (-b,a) ,这样的点 P' 叫做点 P 的“中和点”. (1)、初步体验:
(1)、初步体验:点 A(3,1) 的“中和点 A' ”的坐标是;
(2)、实践应用:已知抛物线 y=-(x+2)2+m与 x 轴交于点 C , D (点 C 在点 D 的左侧),顶点为 E .点 P 在抛物线 y=-(x+2)2+m 上,点 P 的“中和点”为 P' .若点 P' 恰好在抛物线的对称轴上,且四边形ECP'D是菱形,求 m 的值;
(3)、深化拓展:若点 F 是函数 y=-2x-6 ( -4≤x≤-2 )图象上的一点,点 F 的“中和点”为 F' ,连结 FF' ,以 为半径作⊙Q , 求出⊙Q的半径r的取值范围.
24. 如图,抛物线y=x2﹣2x﹣3与x轴相交于A、B两点(A点位于B点左侧),与y轴相交于点C , 点M为抛物线的顶点. (1)、求点A、B、C及顶点M的坐标.(2)、若点N是第四象限内抛物线上的一个动点,连结BN、CN , 求△BCN面积的最大值及此时点N的坐标.(3)、若点D是抛物线对称轴上的动点,点G是抛物线上的动点,是否存在以点B、C、D、G为顶点的四边形是平行四边形.若存在,求出点D的坐标;若不存在,试说明理由.
(1)、求点A、B、C及顶点M的坐标.(2)、若点N是第四象限内抛物线上的一个动点,连结BN、CN , 求△BCN面积的最大值及此时点N的坐标.(3)、若点D是抛物线对称轴上的动点,点G是抛物线上的动点,是否存在以点B、C、D、G为顶点的四边形是平行四边形.若存在,求出点D的坐标;若不存在,试说明理由.