初中数学苏科版七年级上学期期中复习专题7 有理数的混合运算

试卷更新日期：2020-10-25 类型：复习试卷

进入出卷网下载

一、单选题

1. 甲、乙、丙三地海拔高度分别为30米，-25米，-5米，那么最高的地方比最低的地方高（）

A、20米 B、25米 C、35米 D、55米

查看试题解析
2. 马虎同学做了以下4道计算题：①0﹣（﹣1）=1；② $\frac{1}{2}$ ÷（﹣ $\frac{1}{2}$ ）=﹣1；③﹣ $\frac{5}{7}$ + $\frac{2}{7}$ =﹣（ $\frac{5}{7}$ + $\frac{2}{7}$ ）=﹣1；④﹣7﹣2×5=﹣9×5=﹣45.请你帮他检查一下，他一共做对了（）

A、1题 B、2题 C、3题 D、4题

查看试题解析
3. 计算4＋(－8)÷(－4)－(－1) 的结果是（）

A、2 B、3 C、7 D、 $\frac{4}{3}$

查看试题解析
4. 下列计算正确是（）

A、 $| - 2 | - | - 5 | = 3$ B、 ${(- 2)}^{3} \times \frac{1}{2} = 4$ C、 ${(- 1)}^{2019} \times {(- 3)}^{2} = - 9$ D、 $(- 3) \times \frac{1}{3} \div (- 3) \times \frac{1}{3} = 1$

查看试题解析
5. 式子－2²＋(－2)²－(－2)³－2³的值为（）

A、－2 B、6 C、－18 D、0

查看试题解析
6. 用“※”定义新的运算：对于任意有理数a和b，规定a※b=b²-ab，如1※3=3²-1×3=6，则（-2）※（-3）的值为（）

A、3 B、-3 C、6 D、-6

查看试题解析
7. 张三经营一家小商店，一天一位顾客用一张50元的人民币买烟，一盒烟18元，张三找了顾客32元钱，过了一会，张三发现刚才那张50元钱是假币. 若张三卖一盒烟能赚3元钱，在这笔买卖中，张三赔了（）

A、64元 B、52元 C、48元 D、47元

查看试题解析
8. 某校利用二维码进行学生学号统一编排.黑色小正方形表示1，白色小正方形表示0，将每一行数字从左到右依次记为a，b，c，d，那么利用公式 $a \times 2^{3} + b \times 2^{2} + c \times 2^{1} + d$ 计算出每一行的数据.第一行表示年级，第二行表示班级，第三行表示班级学号的十位数，第四行表示班级学号的个位数.如图1所示，第一行数字从左往右依次是1，0，0，1，则表示的数据为1×2³+0×2²+0×2¹+1=9，记作09，第二行数字从左往右依次是1，0，1，0，则表示的数据为1×2³+0×2²+1×2¹=10，记作10，以此类推，图1代表的统一学号为091034，表示9年级10班34号.小明所对应的二维码如图2所示，则他的统一学号为（）.

A、060729 B、070629 C、070627 D、060727

查看试题解析
9. 利用运算律简便计算52×（–999）+49×（–999）+999正确的是（）

A、–999×（52+49）=–999×101=–100899 B、–999×（52+49–1）=–999×100=–99900 C、–999×（52+49+1）=–999×102=–101898 D、–999×（52+49–99）=–999×2=–1998

查看试题解析
10. 如图，在一个由六个圆圈组成的三角形里，把-1，-2，-3，-4，-5，-6这6个数分别填入图中圆圈里，要求三角形每条边上的三个数的和S都相等，那么S的最大值是（）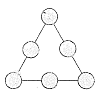

A、-9 B、-10 C、-12 D、-13

查看试题解析

二、填空题

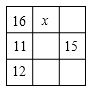
11. 请你用运算符号（包括括号）把2，－6，－9，9 四个数写出一个算式，使它的结果等于24.那么你所列的式子为=24.

查看试题解析
12. 如图，方格表中的格子填上了数，每一行每一列及两条对角线中所填数的和均相等，则x的值是.

查看试题解析
13. 某次数学和测验，以90分为标准，老师公布成绩：小明+10分，小刚0分，小敏﹣2分，则小敏的实际得分是.

查看试题解析
14. 如图，这是一个数值转换机的示意图．若输入x的值为﹣2，输出的结果为4，则输入y的值为．

查看试题解析
15. 在等式 $3 \times □ - 2 \times □ = 15$ 的两个方格中分别填入一个数，使这两个数互为相反数且使等式成立，则第一个方格内的数是.

查看试题解析
16. 如图所示，将形状、大小完全相同的“●”和线段按照一定规律摆成下列图形，第1幅图形中“●”的个数为a₁ ，第2幅图形中“●”的个数为a₂ ，第3幅图形中“●”的个数为a₃ ， …，以此类推，则 $\frac{1}{a_{1}} + \frac{1}{a_{2}} + \frac{1}{a_{3}} + \cdot \cdot \cdot + \frac{1}{a_{8}}$ 的值为

查看试题解析

三、解答题

17. 计算：

(1)、 $3 + (- 11) - (- 9)$

(2)、 ${(- 2)}^{2} + (- 1 - 3) \div (- \frac{2}{3}) + | - \frac{1}{16} | \times (- 2^{4})$

查看试题解析
18. 下面计算是否正确？若错误，错误在第步，并予以改正
$\begin{array}{l} - 2^{2} \times \frac{1}{4} - 9 \div 3 \times \frac{1}{3} \\ = 4 \times \frac{1}{4} - 9 \div 1 \\ = 1 - 9 \\ = - 8 \end{array}$

查看试题解析
19. 某人用400元购买了8套儿童服装，准备以一定的价格出售，如果每套儿童服装以55元的价格为标准，超出的记作正数，不足的记作负数，记录如下（单位：元）：+2，﹣3，+2，+1，﹣2，﹣1，0，﹣2，当他卖完这8套儿童服装后是盈利还是亏损？盈利（或亏损）多少？

查看试题解析
20. 有一种“24点”游戏，其游戏规则是：任取四个 $- 13$ 至13之间（包括13和 $- 13$ ）的不同的整数，将这四个数（每个数用且只用一次）进行有理数的综合运算，使得运算结果等于24.
现在有四个有理数3，4， $- 6$ ，10，运用上述规则写出三个不同的算式.

查看试题解析
21. 某一出租车一天下午以鼓楼为出发点，在东西方向上营运，向东为正，向西为负，行车路程依先后次序记录如下(单位：km)：

＋9

－3

－5

＋4

－8

＋6

－3

－6

－4

＋7

(1)、将最后一名乘客送到目的地，出租车离鼓楼出发点多远？在鼓楼什么方向？

(2)、将最后一名乘客送到目的地，出租车一共行驶多少千米？

(3)、若每千米的价格为2.4元，司机一下午的营运额是多少元？

查看试题解析
22. 如图，现有5张写着不同数的卡片，请按要求完成下列问题：

(1)、从中任选2张卡片，使这2张卡片上的数的乘积最大，则该乘积的最大值是多少?

(2)、从中任选4张卡片，用卡片上的数和加、减、乘、除四则运算(可用括号，每个数都要用且只能用一次)列出两个不同的算式(每个算式可选用不同的卡片)，使其计算结果为24。

查看试题解析
23. 在一个3×3的方格中填写了9个数字，使得每行、每列、每条对角线上的三个数之和相等，得到的3×3的方格称为一个三阶幻方．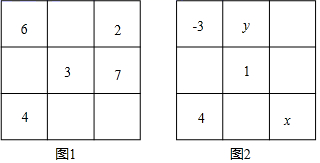

(1)、在图1中空格处填上合适的数字，使它构成一个三阶幻方；

(2)、如图2的方格中填写了一些数和字母，当x+y的值为多少时，它能构成一个三阶幻方．

查看试题解析