初中数学苏科版七年级上学期期中复习专题4 绝对值与相反数

试卷更新日期：2020-10-25 类型：复习试卷

进入出卷网下载

一、单选题

1. 下列各组数中，互为相反数的是（）

A、|+2|与|-2| B、-|+2|与+(-2) C、-(-2)与+(+2) D、|-(-3) |与-|-3|

查看试题解析
2. 在 ${(- 2)}^{3}, - 2^{2}, - (- 2), - | - 2 |, {(- 2)}^{2}$ 中负数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 若|x|=3，|y|=4，则x+y的绝对值是（）

A、7或﹣7 B、1或﹣1 C、7或1 D、7，﹣7，1，﹣1

查看试题解析
4. 若|a|=1，|b|=4，且ab＜0，则a＋b的值为（）

A、±3 B、-3 C、3 D、±5

查看试题解析
5. 下列说法中错误的是（）

A、互为相反数的两个数和为0 B、一个数的相反数必是0或负数 C、 $\frac{3}{2}$ 的倒数的相反数是 $- \frac{2}{3}$ D、负数的相反数是正数

查看试题解析
6. $7 - a$ 的相反数是－2，那么a是（）

A、5 B、－3 C、2 D、1

查看试题解析
7. 若a与b互为相反数，c与d互为倒数，m的绝对值为2，则|m|﹣c×d+ $\frac{a + b}{m}$ 的值（）

A、1 B、﹣2 C、1或﹣3 D、 $\frac{3}{2}$ 或 $\frac{5}{2}$

查看试题解析
8. 实数a，b，c在数轴上的对应点的位置如图所示，那么这三个数中绝对值最大的是（）

A、a B、b C、c D、无法确定

查看试题解析
9. 如图，数轴上有三个点A、B、C，若点A、B表示的数互为相反数，则图中点C对应的数是（）

A、﹣2 B、0 C、1 D、4

查看试题解析
10. 我们规定：在平面直角坐标系xOy中，任意不重合的两点M(x₁ ， y₁)，N(x₂ ， y₂)之间的折线距离为 $d (M ， N) = | x_{1} - x_{2} | + | y_{1} - y_{2} |$ ，例如图①中，点M(－2，3)与点N(1，－1)之间的折线距离为 $d (M ， N) = | - 2 - 1 | + | 3 - (- 1) | = 3 + 4 = 7$ ．如图②，已知点P(3，－4)，若点Q的坐标为(2，t)，且 $d (P ， Q) = 10$ ，则t的值为（）

A、－7或1 B、-5 或13 C、5或－13 D、－1或7

查看试题解析

二、填空题

11. 若m与-2互为相反数，则m的值为。

查看试题解析
12. 5的相反数是；0的相反数是；－2的倒数是

查看试题解析
13. 比较大小：－(－4)－│－4│.

查看试题解析
14. 已知m和n互为相反数，p和q互为倒数，x的绝对值是5，则3（m+n）-pq+x的值为.

查看试题解析
15. 绝对值小于 $π$ 的负整数是.绝对值小于 $π$ 的所有整数的和为.

查看试题解析
16. 已知互不相等的整数a，b，c，d满足abcd＝25，且a＞b＞c＞d，那么 $| a + b | + | c + d |$ ＝.

查看试题解析
17. 如图A，B，C，D，E分别是数轴上五个连续整数所对应的点，其中有一点是原点，数a对应的点在B与C之间，数b对应的点在D与E之间，若 $| a | + | b | = 3$ 则原点可能是．

查看试题解析
18. 有理数a、b、c在数轴上的对应点如图，化简代数式：|a-b|+|a+b|-2|c-a|= ．

查看试题解析

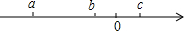
三、解答题

19. 在数轴上表示下列各数，并用“＜”把它们连接起来.
－(－4)，－(＋3.5)，－1.5，0， $| - 2 |$

查看试题解析
20. 若a，b，c都是非零有理数，求 $\frac{a}{| a |} + \frac{b}{| b |} + \frac{c}{| c |}$ 的值．

查看试题解析
21. 已知在数轴上点A、B所表示的数分别为a、b，AB＝3，且|b|=2|a|，求a、b的值.

查看试题解析
22. 在有些情况下，不需要计算出结果也能把绝对值符号去掉，
例如：|6+7|=6+7；|7﹣6|=7﹣6；|6﹣7|=7﹣6；|﹣6﹣7|=6+7.

(1)、根据上面的规律，把下列各式写成去掉绝对值符号的形式：
①|7+21|=；② $| - \frac{1}{2} + 0.8 |$ =；③ $| - 2.8 - \frac{2}{3} |$ =；

(2)、用合理的方法进行简便计算： $| - 9 \frac{1}{33} + 2 \frac{1}{20} | + | - 4 - \frac{1}{20} | - (+ 2 \frac{1}{33})$ ；

(3)、用简单的方法计算： $| \frac{1}{3} - \frac{1}{2} | + | \frac{1}{4} - \frac{1}{3} | + | \frac{1}{5} - \frac{1}{4} | + ... + | \frac{1}{2020} - \frac{1}{2019} | + | \frac{1}{2021} - \frac{1}{2020} |$ .

查看试题解析
23.

(1)、比较下列各式的大小:
|5|+|3||5+3|，|-5|+|-3||（-5）+（-3）|，

|-5|+|3||（-5）+3|，|0|+|-5||0+（-5）|；

(2)、通过（1）的比较、观察，请你猜想归纳:
当a，b为有理数时，|a|+|b||a+b|（填入“≥”“≤”“>”或“<”）；

(3)、根据（2）中你得出的结论，求当|x|+|-2|=|x-2|时，直接写出x的取值范围.

查看试题解析
24. 点A、O、B、C从左向右依次在数轴上的位置如图所示，点O在原点，点A、B、C表示的数分别是a、b、c .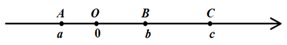

(1)、若a=﹣2，b=4，c=8，D为AB中点，F为BC中点，求DF的长.

(2)、若点A到原点的距离为3，B为AC的中点.
①用b的代数式表示c；

②数轴上B、C两点之间有一动点M，点M表示的数为x，无论点M运动到何处，代数式 |x﹣c|﹣5|x﹣a|+bx+cx 的值都不变，求b的值.

查看试题解析