广东省茂名地区2019-2020学年高二上学期数学期末考试试卷

试卷更新日期：2020-10-23 类型：期末考试

进入出卷网下载

一、单选题

1. 已知向量 $\vec{a} = (1 ， - 1 ， - 2)$ 及 $\vec{b} = (- 4 ， 2 ， 0)$ 则 $\vec{a} + \vec{b}$ 等于（）

A、 $(- 3 ， 1 ， - 2)$ B、 $(5 ， 5 ， - 2)$ C、 $(3 ， - 1 ， 2)$ D、 $(- 5 ， - 5 ， 2)$

查看试题解析
2. 命题“对任意x∈R，都有x²≥0”的否定为（）

A、对任意x∈R，都有x²＜0 B、不存在x∈R，都有x²＜0 C、存在x₀∈R，使得x₀²≥0 D、存在x₀∈R，使得x₀²＜0

查看试题解析
3. 设集合 $M = {1 ， 2}$ ， $N = {a^{2}}$ ，则“ $a = - 1$ ”是“ $N \subseteq M$ ”的（）

A、充分不必要条件 B、必要不充分条件. C、充分必要条件 D、既不充分又不必要条件

查看试题解析
4. 双曲线 $\frac{x^{2}}{3} - y^{2} = 1$ 的焦点坐标是（）

A、(− $\sqrt{2}$ ，0)，( $\sqrt{2}$ ，0) B、(−2，0)，(2，0) C、(0，− $\sqrt{2}$ )，(0， $\sqrt{2}$ ) D、(0，−2)，(0，2)

查看试题解析
5. 椭圆 $\frac{x^{2}}{9}$ + $\frac{y^{2}}{4}$ =1的离心率是（）

A、 $\frac{\sqrt{13}}{3}$ B、 $\frac{\sqrt{5}}{3}$ C、 $\frac{2}{3}$ D、 $\frac{5}{9}$

查看试题解析
6. 已知向量 $\vec{a} = (- 2 ， x ， 2) ， \vec{b} = (2 ， 1 ， 2) ， \vec{c} = (4 ， - 2 ， 1)$ .若 $\vec{a} ⊥ (\vec{b} - \vec{c})$ ，则x的值为（）

A、-2 B、2 C、3 D、-3

查看试题解析
7. 椭圆 $\frac{x^{2}}{25} + \frac{y^{2}}{9} = 1$ 和椭圆 $\frac{x^{2}}{9 - k} + \frac{y^{2}}{25 - k} = 1$ （ $0 < k < 9$ ）有（）

A、等长的长轴 B、相等的焦距 C、相等的离心率 D、等长的短轴

查看试题解析
8. 过抛物线 $y^{2} = 4 x$ 的焦点的直线 $l$ 交抛物线于 $P (x_{1} ， y_{1})$ 、 $Q (x_{2} ， y_{2})$ 两点，如果 $x_{1} + x_{2} = 6$ ，则 $| P Q | =$ （）

A、9 B、6 C、7 D、8

查看试题解析
9. 已知椭圆C： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左右焦点为F₁ ， F₂离心率为 $\frac{\sqrt{3}}{3}$ ，过F₂的直线l交C与A，B两点，若△AF₁B的周长为 $4 \sqrt{3}$ ，则C的方程为（）

A、 $\frac{x^{2}}{3} + \frac{y^{2}}{2} = 1$ B、 $\frac{x^{2}}{3} + y^{2} = 1$ C、 $\frac{x^{2}}{12} + \frac{y^{2}}{8} = 1$ D、 $\frac{x^{2}}{12} + \frac{y^{2}}{4} = 1$

查看试题解析
10. 已知椭圆 $\frac{x^{2}}{36} + \frac{y^{2}}{9} = 1$ 以及椭圆内一点P(4，2)，则以P为中点的弦所在直线的斜率为（）

A、－ $\frac{1}{2}$ B、 $\frac{1}{2}$ C、－2 D、2

查看试题解析
11. 若点O和点F分别为椭圆 $\frac{x^{2}}{4} + \frac{y^{2}}{3} = 1$ 的中心和左焦点，点P为椭圆上点的任意一点，则 $\overset{⇀}{O P} \cdot \overset{⇀}{F P}$ 的最大值为（）

A、2 B、3 C、6 D、8

查看试题解析
12. 数学中有许多形状优美、寓意美好的曲线，曲线C： $x^{2} + y^{2} = 1 + | x | y$ 就是其中之一（如图）.给出下列三个结论：

①曲线C恰好经过6个整点（即横、纵坐标均为整数的点）；②曲线C上任意一点到原点的距离都不超过 $\sqrt{2}$ ；③曲线C所围成的“心形”区域的面积小于3.其中，所有正确结论的序号是（）

A、① B、② C、①② D、①②③

查看试题解析

二、填空题

13. 抛物线 $x^{2} = 4 y$ 的准线方程是

查看试题解析
14. 已知椭圆焦点在x轴上，且 $a = 4$ ， $c = 2$ ，则椭圆方程为.

查看试题解析
15. 已知双曲线C： $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的左、右焦点分别为F₁ ， F₂ ，过F₁的直线与C的两条渐近线分别交于A，B两点．若 $\overset{⇀}{F_{1} A} = \overset{⇀}{A B}$ ， $\overset{⇀}{F_{1} B} \cdot \overset{⇀}{F_{2} B} = 0$ ，则C的离心率为．

查看试题解析

三、双空题

16. 设双曲线经过点（2，2），且与 $\frac{y^{2}}{4} - x^{2} = 1$ 具有相同渐近线，则的方程为；渐近线方程为.

查看试题解析

四、解答题

17. 求符合下列要求的曲线的标准方程：

(1)、已知椭圆的焦点在x轴，且长轴长为12，离心率为 $\frac{1}{2}$ ；

(2)、已知双曲线经过点 $A (- 7 ， - 6 \sqrt{2})$ ， $B = (2 \sqrt{7} ， 3)$ .

查看试题解析
18. 已知向量 $\vec{a} = (1 ， 2 ， - 2)$ ， $\vec{b} = (4 ， - 2 ， 4)$ ， $\vec{c} = (3 ， m ， n)$ .

(1)、求 $\vec{a} - \vec{b}$

(2)、若 $\vec{a} // \vec{c}$ ，求m，n.

(3)、求 $\cos 〈 \vec{a} ， \vec{b} 〉$

查看试题解析
19. 直线l： $y = k x - 1$ ，双曲线C： $x^{2} - \frac{y^{2}}{4} = 1$ ，

(1)、当 $k = 1$ 时，直线l与双曲线C有两个交点A、B，求 $| A B |$ ；

(2)、当k取何值时，直线l与双曲线C没有公共交点.

查看试题解析
20. 如图，长方体ABCD–A₁B₁C₁D₁的底面ABCD是正方形，点E在棱AA₁上，BE⊥EC₁.

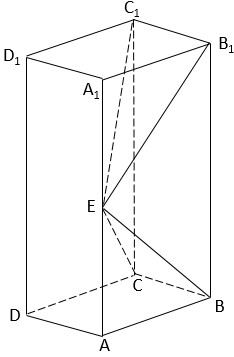(1)、证明：BE⊥平面EB₁C₁；

(2)、若AE=A₁E，求二面角B–EC–C₁的正弦值.

查看试题解析
21. 已知点A(0，－2)，椭圆E： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ (a>b>0)的离心率为 $\frac{\sqrt{3}}{2}$ ，F是椭圆E的右焦点，直线AF的斜率为 $\frac{2 \sqrt{3}}{3}$ ，O为坐标原点.

(1)、求E的方程；

(2)、设过点A的动直线l与E相交于P，Q两点.当△OPQ的面积最大时，求l的方程.

查看试题解析
22. 已知曲线 $Γ$ 上的点到点 $F (0 ， 1)$ 的距离比它到直线 $y = - 3$ 的距离小2.

(1)、求曲线 $Γ$ 的方程；

(2)、曲线 $Γ$ 在点 $P$ 处的切线 $l$ 与 $x$ 轴交于点 $A$ .直线 $y = 3$ 分别与直线 $l$ 及 $y$ 轴交于点 $M ， N$ ，以 $M N$ 为直径作圆 $C$ ，过点 $A$ 作圆 $C$ 的切线，切点为 $B$ ，试探究：当点 $P$ 在曲线 $Γ$ 上运动（点 $P$ 与原点不重合）时，线段 $A B$ 的长度是否发生变化？证明你的结论.

查看试题解析