初中数学北师大版九年级上学期期中考试复习专题:05成比例线段
试卷更新日期:2020-10-23 类型:复习试卷
一、单选题
-
1. 如图,在△ABC中,DE∥AB,且 = ,则 的值为( )
 A、 B、 C、 D、2. 如图,直线a∥b∥c , 分别交直线m , n于点A , B , C , D , E , F , 若AB=2,BC=4,DE=3,则EF的长是( )
A、 B、 C、 D、2. 如图,直线a∥b∥c , 分别交直线m , n于点A , B , C , D , E , F , 若AB=2,BC=4,DE=3,则EF的长是( )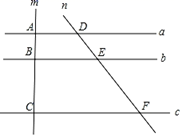 A、5 B、6 C、7 D、83. 如图,在 中,点 分别在 边上,连接 ,若 ,则下列结论错误的是( )
A、5 B、6 C、7 D、83. 如图,在 中,点 分别在 边上,连接 ,若 ,则下列结论错误的是( ) A、 B、 C、 D、4. 下列各组线段中,成比例的是( )A、2cm,3cm,4cm,5cm B、2cm,4cm,6cm,8cm C、3cm,6cm,8cm,12cm D、1cm,3cm,5cm,15cm5. 正方形ABCD的边长AB=2,E为AB的中点,F为BC的中点,AF分别与DE、BD相交于点M , N , 则MN的长为( )
A、 B、 C、 D、4. 下列各组线段中,成比例的是( )A、2cm,3cm,4cm,5cm B、2cm,4cm,6cm,8cm C、3cm,6cm,8cm,12cm D、1cm,3cm,5cm,15cm5. 正方形ABCD的边长AB=2,E为AB的中点,F为BC的中点,AF分别与DE、BD相交于点M , N , 则MN的长为( )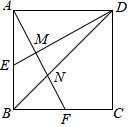 A、 B、 ﹣1 C、 D、
A、 B、 ﹣1 C、 D、二、填空题
-
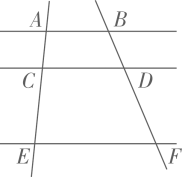
6. 如图, .若 , ,则 .
 7. 若 ,则 .8. 若x∶y∶z=2∶3∶4,则 的值为.9. 如图,已知正方形ABCD的边长为4,E,F分别为AB,CD边上的点,且EF∥BC,G为EF上一点,且GF=1,M,N分别为GD,EC的中点,则MN= 。
7. 若 ,则 .8. 若x∶y∶z=2∶3∶4,则 的值为.9. 如图,已知正方形ABCD的边长为4,E,F分别为AB,CD边上的点,且EF∥BC,G为EF上一点,且GF=1,M,N分别为GD,EC的中点,则MN= 。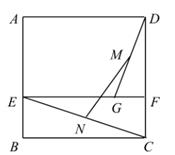
三、综合题
-
10. 如图,在等边△ABC中,已知点E在直线AB上(不与点A、B重合),点D在直线BC上,且ED=EC .
 (1)、若点E为线段AB的中点时,试说明DB=AE的理由;(2)、若△ABC的边长为2,AE=1,求CD的长.11. 如图,矩形 ,延长 至点E,使 ,连接 , ,过点C作 交 的延长线于点F,连接 .
(1)、若点E为线段AB的中点时,试说明DB=AE的理由;(2)、若△ABC的边长为2,AE=1,求CD的长.11. 如图,矩形 ,延长 至点E,使 ,连接 , ,过点C作 交 的延长线于点F,连接 . (1)、求证:四边形 是菱形;(2)、连接 交 于点G.当 , 时,求 的长.12. 已知在Rt△ABC中,∠BAC=90°,CD为∠ACB的平分线,将∠ACB沿CD所在的直线对折,使点B落在点B′处,连结AB',BB',延长CD交BB'于点E,设∠ABC=2α(0°<α<45°).
(1)、求证:四边形 是菱形;(2)、连接 交 于点G.当 , 时,求 的长.12. 已知在Rt△ABC中,∠BAC=90°,CD为∠ACB的平分线,将∠ACB沿CD所在的直线对折,使点B落在点B′处,连结AB',BB',延长CD交BB'于点E,设∠ABC=2α(0°<α<45°). (1)、如图1,若AB=AC,求证:CD=2BE;(2)、如图2,若AB≠AC,试求CD与BE的数量关系(用含α的式子表示);(3)、如图3,将(2)中的线段BC绕点C逆时针旋转角(α+45°),得到线段FC,连结EF交BC于点O,设△COE的面积为S1 , △COF的面积为S2 , 求 (用含α的式子表示).
(1)、如图1,若AB=AC,求证:CD=2BE;(2)、如图2,若AB≠AC,试求CD与BE的数量关系(用含α的式子表示);(3)、如图3,将(2)中的线段BC绕点C逆时针旋转角(α+45°),得到线段FC,连结EF交BC于点O,设△COE的面积为S1 , △COF的面积为S2 , 求 (用含α的式子表示).