初中数学北师大版九年级上学期期中考试复习专题：01 特殊平行四边形

试卷更新日期：2020-10-23 类型：复习试卷

进入出卷网下载

一、单选题

1. 下列命题正确的是（）

A、一组对边平行，另一组对边相等的四边形是平行四边形 B、对角线互相垂直的四边形是菱形 C、一个角为 90°且一组邻边相等的四边形是正方形 D、对角线相等的平行四边形是矩形

查看试题解析
2. 如图，在菱形 $A B C D$ 中，P是对角线 $A C$ 上一动点，过点P作 $P E ⊥ B C$ 于点E. $P F ⊥ A B$ 于点F.若菱形 $A B C D$ 的周长为20，面积为24，则 $P E + P F$ 的值为（）

A、4 B、 $\frac{24}{5}$ C、6 D、 $\frac{48}{5}$

查看试题解析
3. 如图，在矩形 $A B C D$ 中，E是 $C D$ 上的一点， $Δ A B E$ 是等边三角形， $A C$ 交 $B E$ 于点F，则下列结论不成立的是（）

A、 $∠ D A E = 30^{\circ}$ B、 $∠ B A C = 45^{\circ}$ C、 $\frac{E F}{F B} = \frac{1}{2}$ D、 $\frac{A D}{A B} = \frac{\sqrt{3}}{2}$

查看试题解析
4. 如图，在正方形 $A B C D$ 中，对角线 $A C ， B D$ 相交于点O，点E在BC边上，且 $C E = 2 B E$ ，连接AE交BD于点G，过点B作 $B F ⊥ A E$ 于点F，连接OF并延长，交BC于点M，过点O作 $O P ⊥ O F$ 交DC于占N， $S_{四边形 M O N C} = \frac{9}{4}$ ，现给出下列结论：① $\frac{G E}{A G} = \frac{1}{3}$ ；② $\sin ∠ B O F = \frac{3 \sqrt{10}}{10}$ ；③ $O F = \frac{3 \sqrt{5}}{5}$ ；④ $O G = B G$ ；其中正确的结论有（）

A、①②③ B、②③④ C、①②④ D、①③④

查看试题解析
5. 如图，正方形 $A B C D$ 中，点F是 $B C$ 边上一点，连接 $A F$ ，以 $A F$ 为对角线作正方形 $A E F G$ ，边 $F G$ 与正方形 $A B C D$ 的对角线 $A C$ 相交于点H，连接 $D G$ ．以下四个结论：① $∠ E A B = ∠ G A D$ ；② $Δ A F C \sim Δ A G D$ ；③ $2 A E^{2} = A H \cdot A C$ ；④ $D G ⊥ A C$ ．其中正确的个数为（）

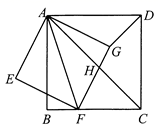A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

6. 如图，菱形ABCD的周长为16，AC，BD交于点O，点E在BC上，OE∥AB，则OE的长是.

查看试题解析
7. 如图，在长方形ABCD中，AB＝12，BC＝9，P为AD上一点，将△ABP沿BP翻折至△EBP，PE与CD相交于点O，且OE＝OD，则AP＝.

查看试题解析
8. 如图，矩形ABCD中，AD=12，AB=8，E是AB上一点，且EB=3，F是BC上一动点，若将 $Δ E B F$ 沿EF对折后，点B落在点P处，则点P到点D的最短距为．

查看试题解析
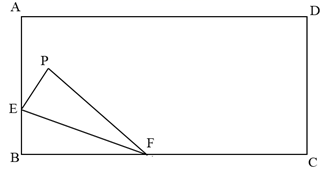9. 如图，矩形纸片ABCD，AB＝6cm，BC＝8cm，E为边CD上一点．将△BCE沿BE所在的直线折叠，点C恰好落在AD边上的点F处，过点F作FM⊥BE，垂足为点M，取AF的中点N，连接MN，则MN＝cm．

查看试题解析
10. 如图，将边长为4的正方形ABCD沿着折痕EF折叠，使点B落在边AD的中点G处，则BE的长为.

查看试题解析

三、综合题

11. 如图，已知AD是△ABC的角平分线，DE∥AC交AB于点E，DF∥AB交AC于点F.

(1)、求证：四边形AEDF是菱形；

(2)、请直接填写，当∠BAC=°时，四边形AEDF是正方形.

查看试题解析
12. 如图，在矩形 $A B C D$ 中， $O$ 为对角线 $A C$ 的中点，过点 $O$ 作直线分别与矩形的边 $A D$ ， $B C$ 交于 $M$ ， $N$ 两点，连接 $C M$ ， $A N$ ．

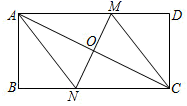(1)、求证：四边形 $A N C M$ 为平行四边形；

(2)、若 $A D = 4$ ， $A B = 2$ ，且 $M N ⊥ A C$ ，求 $D M$ 的长

查看试题解析
13. 如图1，在矩形ABCD中，AB＝5，BC＝8，点E，F分别为AB，CD的中点.

(1)、求证：四边形AEFD是矩形；

(2)、如图2，点P是边AD上一点，BP交EF于点O，点A关于BP的对称点为点M，当点M落在线段EF上时，则有OB＝OM.请说明理由；

(3)、如图3，若点P是射线AD上一个动点，点A关于BP的对称点为点M，连接AM，DM，当△AMD是等腰三角形时，求AP的长.

查看试题解析
14. 如图，正方形 $A B C D$ 的边长为6， $M$ 为 $A B$ 的中点， $△ M B E$ 为等边三角形，过点 $E$ 作 $M E$ 的垂线分别与边 $A D$ 、 $B C$ 相交于点 $F$ 、 $G$ ，点 $P$ 、 $Q$ 分别在线段 $E F$ 、 $B C$ 上运动，且满足 $∠ P M Q = 60 °$ ，连接 $P Q$ .

(1)、求证： $△ M E P ≅ △ M B Q$ .

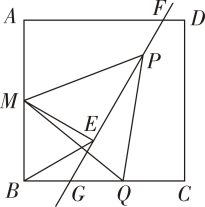(2)、当点 $Q$ 在线段 $G C$ 上时，试判断 $P F + G Q$ 的值是否变化？如果不变，求出这个值，如果变化，请说明理由.

(3)、设 $∠ Q M B = α$ ，点 $B$ 关于 $Q M$ 的对称点为 $B^{'}$ ，若点 $B^{'}$ 落在 $Δ M P Q$ 的内部，试写出 $α$ 的范围，并说明理由.

查看试题解析
15. 如图，四边形ABCD中，对角线AC与BD交于点O，且OA＝OB＝OC＝OD＝ $\frac{\sqrt{2}}{2}$ AB.

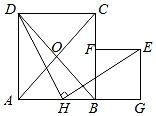(1)、求证：四边形ABCD是正方形；

(2)、若H是边AB上一点（H与A，B不重合），连接DH，将线段DH绕点H顺时针旋转90°，得到线段HE，过点E分别作BC及AB延长线的垂线，垂足分别为F，G.设四边形BGEF的面积为s₁ ，以HB，BC为邻边的矩形的面积为s₂ ，且s₁＝s₂.当AB＝2时，求AH的长.

查看试题解析