初中数学人教版九年级上学期期中考试复习专题:05 旋转、中心对称
试卷更新日期:2020-10-23 类型:复习试卷
一、单选题
-
1. 下列图形绕某一点旋转一定角度都能与原图形重合,其中旋转角度最小的是 ( )A、等边三角形
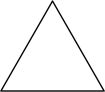 B、平行四边形
B、平行四边形  C、正八边形
C、正八边形 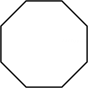 D、圆及其一条弦
D、圆及其一条弦 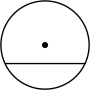 2. 下列垃圾分类标识的图案既是轴对称图形,又是中心对称图形的是( )A、
2. 下列垃圾分类标识的图案既是轴对称图形,又是中心对称图形的是( )A、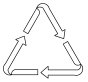 B、
B、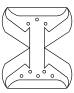 C、
C、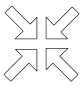 D、
D、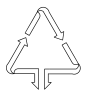 3. 在下图的四个三角形中,不能由 经过旋转或平移得到的是( )
3. 在下图的四个三角形中,不能由 经过旋转或平移得到的是( )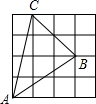 A、
A、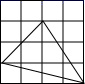 B、
B、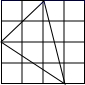 C、
C、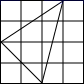 D、
D、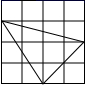 4. 在平面直角坐标系中,点 关于原点对称的点的坐标是( )A、 B、 C、 D、5. 如图,△ABC中,∠ACB=90°,∠ABC=40°,将△ABC绕点B逆时针旋转得到△A'BC',使点C的对应点C'恰好落在边AB上,则∠CAA'的度数是( )
4. 在平面直角坐标系中,点 关于原点对称的点的坐标是( )A、 B、 C、 D、5. 如图,△ABC中,∠ACB=90°,∠ABC=40°,将△ABC绕点B逆时针旋转得到△A'BC',使点C的对应点C'恰好落在边AB上,则∠CAA'的度数是( )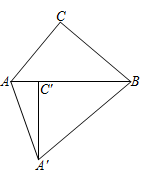 A、50° B、70° C、110° D、120°6. 如图,等腰三角形ABC中,∠ABC=90°,BA=BC,将BC绕点B顺时针旋转θ(0°<θ<90°),得到BP,连结CP,过点A作AH⊥CP交CP的延长线于点H,连结AP,则∠PAH的度数( )
A、50° B、70° C、110° D、120°6. 如图,等腰三角形ABC中,∠ABC=90°,BA=BC,将BC绕点B顺时针旋转θ(0°<θ<90°),得到BP,连结CP,过点A作AH⊥CP交CP的延长线于点H,连结AP,则∠PAH的度数( )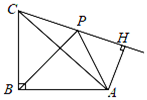 A、随着θ的增大而增大 B、随着θ的增大而减小 C、不变 D、随着θ的增大,先增大后减小7. 如图,矩形ABCD中,AB=2 ,BC=6,P为矩形内一点,连接PA,PB,PC,则PA+PB+PC的最小值是( )
A、随着θ的增大而增大 B、随着θ的增大而减小 C、不变 D、随着θ的增大,先增大后减小7. 如图,矩形ABCD中,AB=2 ,BC=6,P为矩形内一点,连接PA,PB,PC,则PA+PB+PC的最小值是( )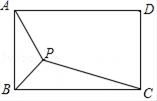 A、4 +3 B、2 C、2 +6 D、4
A、4 +3 B、2 C、2 +6 D、4二、填空题
-
8. 点A(-2,3)关于y轴,原点O对称的点的坐标分别是 . 线段AO= .9. 如图,在 中, , .将 绕点B逆时针旋转60°,得到 ,则 边的中点D与其对应点 的距离是.
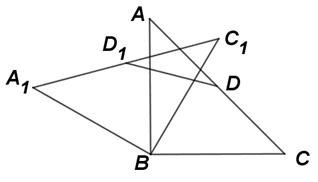 10. 点O是正五边形ABCDE的中心,分别以各边为直径向正五边形的外部作半圆,组成了一幅美丽的图案(如图).这个图案绕点O至少旋转°后能与原来的图案互相重合.
10. 点O是正五边形ABCDE的中心,分别以各边为直径向正五边形的外部作半圆,组成了一幅美丽的图案(如图).这个图案绕点O至少旋转°后能与原来的图案互相重合.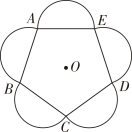 11. 用四块大正方形地砖和一块小正方形地砖拼成如图所示的实线图案,每块大正方形地砖面积为a,小正方形地砖面积为b. 依次连接四块大正方形地砖的中心得到正方形ABCD. 则正方形ABCD的面积为. (用含a,b的代数式表示)
11. 用四块大正方形地砖和一块小正方形地砖拼成如图所示的实线图案,每块大正方形地砖面积为a,小正方形地砖面积为b. 依次连接四块大正方形地砖的中心得到正方形ABCD. 则正方形ABCD的面积为. (用含a,b的代数式表示)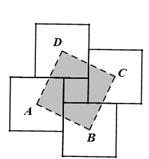
三、作图题
-
12. 如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系中, 的三个顶点 、 、 均在格点上
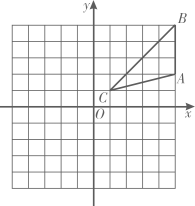 (1)、将 向左平移5个单位得到 ,并写出点 的坐标;(2)、画出 绕点 顺时针旋转 后得到的 ,并写出点 的坐标;(3)、在(2)的条件下,求 在旋转过程中扫过的面积(结果保留 ).13. 如图,在平面直角坐标系中,△ABC的三个顶点分别是A(1,3),B(4,4),C(2,1).
(1)、将 向左平移5个单位得到 ,并写出点 的坐标;(2)、画出 绕点 顺时针旋转 后得到的 ,并写出点 的坐标;(3)、在(2)的条件下,求 在旋转过程中扫过的面积(结果保留 ).13. 如图,在平面直角坐标系中,△ABC的三个顶点分别是A(1,3),B(4,4),C(2,1). (1)、①把△ABC向左平移4个单位后得到对应的△A1B1C1 , 请画出平移后的△A1B1C1;
(1)、①把△ABC向左平移4个单位后得到对应的△A1B1C1 , 请画出平移后的△A1B1C1;②把△ABC绕原点O旋转180°后得到对应的△A2B2C2 , 请画出旋转后的△A2B2C2;
(2)、观察图形可知,△A1B1C1与△A2B2C2关于点( , )中心对称.四、综合题
-
14. 如图,点M, 分别在正方形 的边 , 上,且 ,把 绕点A顺时针旋转 得到 .
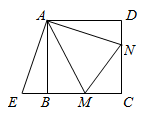 (1)、求证: ≌ .(2)、若 , ,求正方形 的边长.
(1)、求证: ≌ .(2)、若 , ,求正方形 的边长.