初中数学人教版九年级上学期期中考试复习专题：04 二次函数的应用

试卷更新日期：2020-10-23 类型：复习试卷

进入出卷网下载

一、单选题

1. 如图，已知点A（2.18，-0.51）、B（2.68，0.54）在二次函数y=ax²+bx+c（a≠0）的图象上，则方程ax²+bx+c=0的一个近似解可能是（）

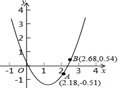A、2.18 B、2.68 C、-0.51 D、2.45

查看试题解析
2. 在平面直角坐标系中，已知函数y₁=x²+ax+1，y₂=x²+bx+2，y₃=x²+cx+4，其中a，b，c是正实数，且满足b²=ac。设函数y₁ ， y₂ ， y₃的图象与x轴的交点个数分别为M₁ ， M₂ ， M₃ ，（）

A、若M₁=2，M₂=2，则M₃=0 B、若M₁=1，M₂=0，则M₃=0 C、若M₁=0，M₂=2，则M₃=0 D、若M₁=0，M₂=0，则M₃=0

查看试题解析
3. 已知 $b > 0$ ，二次函数 $y = a x^{2} + b x + a^{2} - 1$ 的图象为下列之一，则a的值为（）

A、1 B、-1 C、 $\frac{- 1 - \sqrt{5}}{2}$ D、 $\frac{- 1 + \sqrt{5}}{2}$

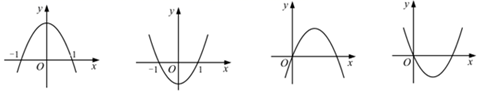查看试题解析
4. 从地面竖直向上抛出一个小球，小球的高度h（单位：m）与小球运动时间（单位：s）之间的函数关系如图所示，
下列结论：①小球在空中经过的路程是40m；②小球抛出3秒后，速度越来越快；③小球抛出3秒时速度为0；④小球的高度h=30m时，t=1.5s．其中正确的是（）

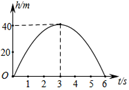A、①④ B、①② C、②③④ D、②③

查看试题解析
5. 三孔桥横截面的三个孔都呈抛物线形，两小孔形状、大小完全相同．当水面刚好淹没小孔时，大孔水面宽度为10米，孔顶离水面1.5米；当水位下降，大孔水面宽度为14米时，单个小孔的水面宽度为4米，若大孔水面宽度为20米，则单个小孔的水面宽度为（）

A、4 $\sqrt{3}$ 米 B、5 $\sqrt{2}$ 米 C、2 $\sqrt{13}$ 米 D、7米

查看试题解析

二、填空题

6. 二次函数y＝ax²+bx+c的图象如图所示，下列结论：①ab＞0；②a+b﹣1＝0；③a＞1；④关于x的一元二次方程ax²+bx+c＝0的一个根为1，另一个根为﹣ $\frac{1}{a}$ ．其中正确结论的序号是．

查看试题解析

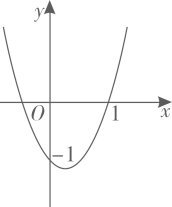7. 已知二次函数y＝ax²＋bx＋c(a≠0)中，函数值y与自变量x的部分对应值如下表：

x	…	－5	－4	－3	－2	－1	…
y	…	3	－2	－5	－6	－5	…

则关于x的一元二次方程ax²＋bx＋c＝－2的根是.

查看试题解析

8. 已知一元二次方程 $(x - 1) (x - 3) = 5$ 的两个实数根分别为 $x_{1}$ ， $x_{2}$ .则抛物线 $y = (x - x_{1}) (x - x_{2}) + 5$ 与x轴的交点坐标为.

查看试题解析
9. 如图，若被击打的小球的飞行高度h（单位：m）与飞行时间t（单位：s）之间的关系为h=20t-5t² ，则小球从飞出到落地所用时间为s

查看试题解析

三、解答题

10. 某商场将进价40元一个的某种商品按50元一个售出时，每月能卖出500个，商场想了两个方案来增加利润:
方案一提高价格，但这种商品每个售价涨价1元，销售量就减少10个；

方案二:售价不变，但发资料做广告，已知这种商品每月的广告费用m（千元）与销售量倍数p关系为p=-0.4m²+2m，

试通过计算，请你判断商场为赚得更大的利润应选择哪种方案?请说明你判断的理由.

查看试题解析
11. 画出函数y=-2x²+8x-6的图象，根据图象回答问题：

(1)、方程-2x²+8x-6=0的解是什么；

(2)、当x取何值时，y＞0；

(3)、当x取何值时，y＜0．

查看试题解析

四、综合题

12. 已知抛物线y＝ax²+bx+c经过A（2，0），B（3n﹣4，y₁），C（5n+6，y₂）三点，对称轴是直线x＝1.关于x的方程ax²+bx+c＝x有两个相等的实数根.

(1)、求抛物线的解析式；

(2)、若n＜﹣5，试比较y₁与y₂的大小；

(3)、若B，C两点在直线x＝1的两侧，且y₁＞y₂ ，求n的取值范围.

查看试题解析
13. 小红经营的网店以销售文具为主，其中一款笔记本进价为每本10元，该网店在试销售期间发现，每周销售数量 $y$ （本）与销售单价 $x$ （元）之间满足一次函数关系，三对对应值如下表：

销售单价 $x$ （元）

12

14

16

每周的销售量 $y$ （本）

500

400

300

(1)、求 $y$ 与 $x$ 之间的函数关系式；

(2)、通过与其他网店对比，小红将这款笔记本的单价定为 $x$ 元（ $12 ⩽ x ⩽ 15$ ，且 $x$ 为整数），设每周销售该款笔记本所获利润为 $w$ 元，当销售单价定为多少元时每周所获利润最大，最大利润是多少元？

查看试题解析
14. 因疫情防控需要，消毒用品需求量增加．某药店新进一批桶装消毒液，每桶进价50元，每天销售量y（桶）与销售单价x（元）之间满足一次函数关系，其图象如图所示．

(1)、求y与x之间的函数表达式；

(2)、每桶消毒液的销售价定为多少元时，药店每天获得的利润最大，最大利润是多少元？（利涧=销售价-进价）

查看试题解析

销售单价 $x$ （元）	12	14	16
每周的销售量 $y$ （本）	500	400	300