初中数学人教版八年级上学期期中考试复习专题：03 全等三角形
试卷更新日期：2020-10-23 类型：复习试卷
一、单选题
-
1. 已知△ABC≌△DEF，点A与D，点C与F分别是对应点，则∠B的对应角是（ ）A、∠A B、∠F C、∠E D、∠C2. 如图，在△ABC中，AC＝5，BC＝12，AB＝13，AD是角平分线，DE⊥AB，垂足为E，则△BDE的周长为（ ）
A、17 B、18 C、20 D、253. 如图，点E，点F在直线AC上， AE＝CF， AD＝CB，下列条件中不能判断△ADF≌△CBE的是（ ）
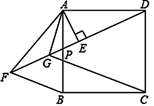
A、AD//BC B、BE//DF C、BE＝DF D、∠A＝∠C4. 如图，在 中， 是AC上一点， 于点E， 连接BD，若AC=8cm，则 等于（ ）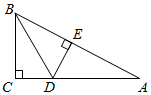
A、6cm B、7cm C、8cm D、9cm5. 如图，在正方形 中，点E，F分别在 ， 上， ， 与 相交于点G.下列结论：① 垂直平分 ；② ；③当 时， 为等边三角形；④当 时， .其中正确的结论是（ ）
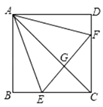A、①③ B、②④ C、①③④ D、②③④6. 下列所叙述的图形中，全等的两个三角形是（ ）A、含有45°角的两个直角三角形 B、腰相等的两个等腰三角形 C、边长相等的两个等边三角形 D、一个钝角对应相等的两个等腰三角形7. 如图，在平行四边形ABCD中，E为BC边上一点（不与端点重合），若AB＝AE ， 且AE平分∠DAB ， 则下列结论：①∠B＝60°，②AC＝BC ， ③∠AED＝∠ACD ， ④△ABC≌△EAD ． 其中正确的个数是（ ）
A、1个 B、2个 C、3个 D、4个二、填空题
-
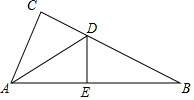
8. 如图，C为线段AE上一动点（不与点A，E重合），在AE同侧分别作正△ABC和正△CDE，AD与BE交于点O，AD与BC交于点P，BE与CD交于点Q，连结PQ.以下五个结论：①AD=BE；②PQ∥AE；③AP=BQ；④DE=DP；⑤∠AOB=60°.恒成立的结论有.（把你认为正确的序号都填上）
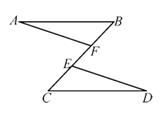
9. 如图，点D，E分别在线段AB，AC上，BE，CD相交于点O，AE = AD，要使△ABE≌△ACD，需添加一个条件是（只需一个即可，图中不能再添加其他点或线）.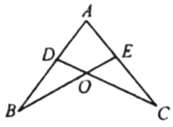
10. 如图， 和 中， ，在不添加任何辅助线的情况下，请你添加一个条件 ， 使 和 全等．
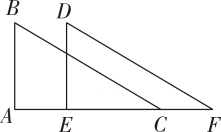11. 我国古代伟大的数学家刘徽将勾股形（古人称直角三角形为勾股形）分割成一个正方形和两对全等的直角三角形，得到一个恒等式，后人借助这种分割方法所得的图形证明了勾股定理，如图所示的就用了这种分割方法，若BD=3，AE=4，则正方形ODCE的边长等于 ．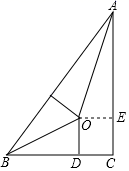
三、解答题
-
12. 如图△ABD≌△EBC，AB=3cm，BC=5cm，求DE的长.
13. 如图，△ABC≌△ADE，且∠CAD=35°，∠B=∠D=20°，∠EAB=105°，求∠BFD和∠BED的度数.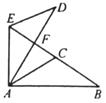
四、综合题
