初中数学浙教版九年级上学期期中复习专题1 二次函数的图象与性质
试卷更新日期:2020-10-22 类型:复习试卷
一、单选题
-
1. 下列函数解析式中,一定为二次函数的是( )A、 B、 C、 D、2. 用配方法将y= x2+x﹣1写成y=a(x﹣h)2+k的形式是( )A、y= (x+1)2﹣1 B、y= (x﹣1)2﹣1 C、y= (x+1)2﹣3 D、y= (x+1)2﹣3. 已知二次函数 ,则下列关于这个函数图象和性质的说法,正确的是( )A、图象的开口向上 B、图象的顶点坐标是 C、当 时,y随x的增大而增大 D、图象与x轴有唯一交点4. 将抛物线 向左平移3个单位长度,再向下平移2个单位长度,得到抛物线的解析式是( )A、 B、 C、 D、5. 如图,直线 交x轴、y轴于A、B两点,点P为线段AB上的点,过点P作 轴于点E,作 轴于点F, ,将线段AB沿y轴负方向向下移动a个单位,线段 扫过矩形 的面积为Z,则下图描述Z与a的函数图象可能是( )
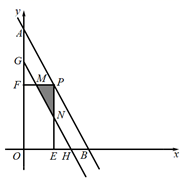 A、
A、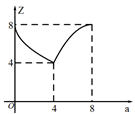 B、
B、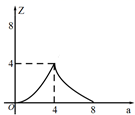 C、
C、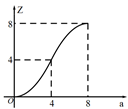 D、
D、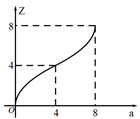 6. 函数 的图象与x轴交于点(2,0),顶点坐标为(-1,n),其中 ,以下结论正确的是( )
6. 函数 的图象与x轴交于点(2,0),顶点坐标为(-1,n),其中 ,以下结论正确的是( )① ;
②函数 在 处的函数值相等;
③函数 的图象与的函数 图象总有两个不同的交点;
④函数 在 内既有最大值又有最小值.
A、①③ B、①②③ C、①④ D、②③④7. 如图,一段抛物线y=﹣x2+4(﹣2≤x≤2)为C1 , 与x轴交于A0 , A1两点,顶点为D1;将C1绕点A1旋转180°得到C2 , 顶点为D2;C1与C2组成一个新的图象,垂直于y轴的直线l与新图象交于点P1(x1 , y1),P2(x2 , y2),与线段D1D2交于点P3(x3 , y3),设x1 , x2 , x3均为正数,t=x1+x2+x3 , 则t的取值范围是( ) A、6<t≤8 B、6≤t≤8 C、10<t≤12 D、10≤t≤128. 若关于x的一元二次方程x2+bx+c=0的两个实数根分别为x1=-1,x2=2,则抛物线y=x2+bx+c的对称轴为直线( )A、x=1 B、x= C、x= D、x=9. “闻起来臭,吃起来香”的臭豆腐是长沙特色小吃,臭豆腐虽小,但制作流程却比较复杂,其中在进行加工煎炸臭豆腐时,我们把焦脆而不糊的豆腐块数的百分比称为“可食用率”,在特定条件下,“可食用率”p与加工煎炸的时间t(单位:分钟)近似满足函数关系式: ( a,b,c为常数),如图纪录了三次实验数据,根据上述函数关系和实验数据,可以得到加工煎炸臭豆腐的最佳时间为( )
A、6<t≤8 B、6≤t≤8 C、10<t≤12 D、10≤t≤128. 若关于x的一元二次方程x2+bx+c=0的两个实数根分别为x1=-1,x2=2,则抛物线y=x2+bx+c的对称轴为直线( )A、x=1 B、x= C、x= D、x=9. “闻起来臭,吃起来香”的臭豆腐是长沙特色小吃,臭豆腐虽小,但制作流程却比较复杂,其中在进行加工煎炸臭豆腐时,我们把焦脆而不糊的豆腐块数的百分比称为“可食用率”,在特定条件下,“可食用率”p与加工煎炸的时间t(单位:分钟)近似满足函数关系式: ( a,b,c为常数),如图纪录了三次实验数据,根据上述函数关系和实验数据,可以得到加工煎炸臭豆腐的最佳时间为( ) A、3.50分钟 B、4.05分钟 C、3.75分钟 D、4.25分钟10. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①b2﹣4ac>0;②abc<0;③4a+b=0;④4a﹣2b+c>0.其中正确结论的个数是( )
A、3.50分钟 B、4.05分钟 C、3.75分钟 D、4.25分钟10. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①b2﹣4ac>0;②abc<0;③4a+b=0;④4a﹣2b+c>0.其中正确结论的个数是( ) A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题
-
11. 下表中y与x的数据满足我们初中学过的某种函数关系,其函数表达式为 .
……
-1
0
1
3
……
……
0
3
4
0
……
12. 二次函数y=a(x+1)(x-4)的对称轴是直线.13. 在平面直角坐标系中,已知 和 是抛物线 上的两点,将抛物线 的图象向上平移n(n是正整数)个单位,使平移后的图象与x轴没有交点,则n的最小值为 .14. 已知二次函数y=ax2+bx+c(a≠0)经过点A(1,-1)、B(3,3),且当1≤x≤3时,-1≤y≤3,则a的取值范围是15. 将抛物线 向左平移1个单位,再向上平移3个单位,则平移后的抛物线的表达式为 .16. 已知二次函数y=ax2﹣2ax+c(a<0)图象上的两点(x1 , y1)和(3,y2),若y1>y2 , 则x1的取值范围是.17. 二次函数 的图象经过点 , , ,与 轴的负半轴相交,且交点在 的上方.下列四个结论中一定正确的是.① ;② ;③ ;④ .(填序号即可)
18. 如图,在平面直角坐标系中,抛物线y=a(x-2)²+1(a为常数)的顶点为A,过点A作y轴的平行线与抛物线y= x2- x交于点B,抛物线y= x2- x的顶点为C,连结CA、CB,则△ABC的面积为 。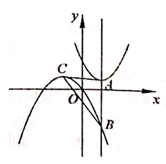
三、解答题
-
19. 二次函数y=ax2+bx+c(a≠0)的图象过点A(﹣1,8)、B(2,﹣1),与y轴交于点C(0,3),求二次函数的表达式.20. 已知二次函数的顶点坐标为 ,且其图象经过点 ,求此二次函数的解析式.21. 定义{a,b,c}为函数y=ax2 +bx+c的“特征数”.如:函数 的“特征数”是{1,-2,3}.将“特征数”为{1,-4,1}的函数图象先向左平移3个单位,再向下平移2个单位得到一个新函数图象,求这个新函数图象的解析式.22. 在平面直角坐标系是,抛物线y=x2+bx+c经过点(1,-2)、(2,-3)。(1)、求这条抛物线所对应的函数表达式(2)、点P是这条抛物线上一点, 其横、纵坐标互为相反数,求点P的坐标。23. 已知,在平面直角坐标系中,抛物线 的顶点为A,点B的坐标为
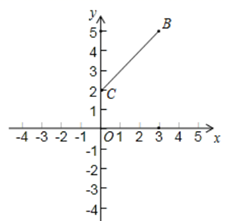 (1)、求抛物线过点B时顶点A的坐标(2)、点A的坐标记为 ,求y与x的函数表达式;(3)、已知C点的坐标为 ,当m取何值时,抛物线 与线段 只有一个交点24. 如图,在平面直角坐标系 xOy 中,已知直线 与x轴交于点A,与y轴交于点B,过A、B两点的抛物线 与x轴交于另一点 .
(1)、求抛物线过点B时顶点A的坐标(2)、点A的坐标记为 ,求y与x的函数表达式;(3)、已知C点的坐标为 ,当m取何值时,抛物线 与线段 只有一个交点24. 如图,在平面直角坐标系 xOy 中,已知直线 与x轴交于点A,与y轴交于点B,过A、B两点的抛物线 与x轴交于另一点 . (1)、求抛物线的解析式;(2)、在抛物线上是否存在一点P,使 ?若存在,请求出点P的坐标,若不存在,请说明理由;(3)、点M为直线 下方抛物线上一点,点N为y轴上一点,当 的面积最大时,求 的最小值.25. 如图,抛物线 与 轴相交于A,B两点,与y轴相交于点C, , ,直线l是抛物线的对称轴,在直线l右侧的抛物线上有一动点D,连接 , , , .
(1)、求抛物线的解析式;(2)、在抛物线上是否存在一点P,使 ?若存在,请求出点P的坐标,若不存在,请说明理由;(3)、点M为直线 下方抛物线上一点,点N为y轴上一点,当 的面积最大时,求 的最小值.25. 如图,抛物线 与 轴相交于A,B两点,与y轴相交于点C, , ,直线l是抛物线的对称轴,在直线l右侧的抛物线上有一动点D,连接 , , , . (1)、求抛物线的函数表达式;(2)、若点D在x轴的下方,当 的面积是 时,求 的面积;(3)、在(2)的条件下,点M是x轴上一点,点N是抛物线上一动点,是否存在点N,使得以点B,D,M,N为顶点,以 为一边的四边形是平行四边形,若存在,求出点N的坐标;若不存在,请说明理由.
(1)、求抛物线的函数表达式;(2)、若点D在x轴的下方,当 的面积是 时,求 的面积;(3)、在(2)的条件下,点M是x轴上一点,点N是抛物线上一动点,是否存在点N,使得以点B,D,M,N为顶点,以 为一边的四边形是平行四边形,若存在,求出点N的坐标;若不存在,请说明理由.