人教A版(2019) 必修一 3.2 函数的性质——奇偶性
试卷更新日期:2020-10-21 类型:同步测试
一、单选题
-
1. 函数 的图象大致为( )A、
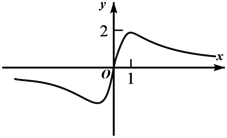 B、
B、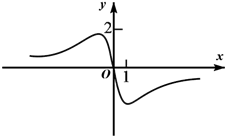 C、
C、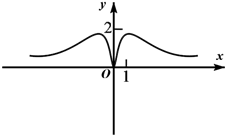 D、
D、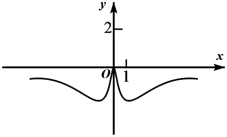 2. 定义在R上的偶函数 满足对任意的 ,有 .则满足 的 取值范围是( )A、 B、 C、 D、3. 已知 是定义在R上的偶函数,并满足 ,当 时, ,则 ( )A、4.5 B、-4.5 C、0.5 D、-0.54. 下列函数中,既是奇函数又是区间(0,+∞)上的增函数的是( )A、 B、y=x﹣1 C、y=x3 D、y=2x5. 已知函数 ,则( )A、 是偶函数,且在 上是增函数 B、 是偶函数,且在 上是减函数 C、 是奇函数,且在 上是增函数 D、 是奇函数,且在 上是减函数6. 已知 是定义在 上的奇函数,且当 时, .若 ,则 的解集是( )A、 B、 C、 D、7. 奇函数 在 上单调递减,且 ,则不等式 的解集是( ).A、 B、 C、 D、8. 已知定义域为R的函数 在 单调递增,且 为偶函数,若 ,则不等式 的解集为( )A、 B、 C、 D、9. 关于函数 的下列判断,其中正确的是( )A、函数的图象是轴对称图形 B、函数的图象是中心对称图形 C、函数有最大值 D、当 时, 是减函数10. 已知定义在 上的函数 满足 ,且在 上是增函数,不等式 对于 恒成立,则 的取值范围是( )A、 B、 C、 D、11. 已知函数 为定义城为 的偶函数,且满足 ,当 时, ,则函数 在区间 上零点的个数为( )A、 B、 C、 D、12. 下列函数 是 上的偶函数,且在 上单调递减,则下列各式成立的是( )A、 B、 C、 D、
2. 定义在R上的偶函数 满足对任意的 ,有 .则满足 的 取值范围是( )A、 B、 C、 D、3. 已知 是定义在R上的偶函数,并满足 ,当 时, ,则 ( )A、4.5 B、-4.5 C、0.5 D、-0.54. 下列函数中,既是奇函数又是区间(0,+∞)上的增函数的是( )A、 B、y=x﹣1 C、y=x3 D、y=2x5. 已知函数 ,则( )A、 是偶函数,且在 上是增函数 B、 是偶函数,且在 上是减函数 C、 是奇函数,且在 上是增函数 D、 是奇函数,且在 上是减函数6. 已知 是定义在 上的奇函数,且当 时, .若 ,则 的解集是( )A、 B、 C、 D、7. 奇函数 在 上单调递减,且 ,则不等式 的解集是( ).A、 B、 C、 D、8. 已知定义域为R的函数 在 单调递增,且 为偶函数,若 ,则不等式 的解集为( )A、 B、 C、 D、9. 关于函数 的下列判断,其中正确的是( )A、函数的图象是轴对称图形 B、函数的图象是中心对称图形 C、函数有最大值 D、当 时, 是减函数10. 已知定义在 上的函数 满足 ,且在 上是增函数,不等式 对于 恒成立,则 的取值范围是( )A、 B、 C、 D、11. 已知函数 为定义城为 的偶函数,且满足 ,当 时, ,则函数 在区间 上零点的个数为( )A、 B、 C、 D、12. 下列函数 是 上的偶函数,且在 上单调递减,则下列各式成立的是( )A、 B、 C、 D、二、填空题
-
13. 已知 是定义在 上的偶函数,且当 时, ,则当 时, .14. 已知 是R上的奇函数,当 时, ,则 的值为 .15. 已知函数 在R上是奇函数,且当 时, ,则 时, 的解析式为.16. 已知f(x)是R上的奇函数,当x≥0时,f(x)=x2﹣5x,则f(x﹣1)>f(x)的解集为 .
三、解答题
-
17. 已知函数 是奇函数.(1)、求实数m的值;(2)、若函数 在区间 上是单调增函数,求实数a的取值范围;(3)、求不等式 的解集.18. 已知(1)、判断函数 的奇偶性,并说明理由.(2)、判断函数 在 单调性,并证明你的判断.19. 已知定义在R上的函数 满足:① 对任意 , ,有 .②当 时, 且 .(1)、求证: 是奇函数;(2)、解不等式 .