初中数学浙教版八年级上学期期中复习专题9 勾股定理
试卷更新日期:2020-10-21 类型:复习试卷
一、单选题
-
1. 在△ABC,∠A,∠B,∠C的对应边分别是a,b,c,若∠B=90°,则下列等式中成立的是( )A、a2+b2=c2 B、b2+c2=a2 C、 a2+c2=b2 D、c2- a2= b22. 如图,在3×3的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,若BD是△ABC的高,则BD的长为( )
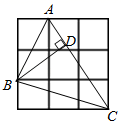 A、 B、 C、 D、3. 下列各组线段a、b、c中不能组成直角三角形的是( )A、a=8,b=15,c=17 B、a=7,b=24,c=25 C、a=40,b=50,c=60 D、a= ,b=4,c=54. 在△ABC中,BC=5,AC=4,AB=3,则( )A、∠A=90° B、∠B=90° C、∠C=90° D、∠A+∠B=90°5. 2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的弦图,它是由四个全等的直角三角形和中间的小正方形拼成的一个大正方形,如图所示,如果大正方形的面积是34,小正方形的面积是4,直角三角形较短的直角边是a,较长的直角边是b,那么 的值为( )
A、 B、 C、 D、3. 下列各组线段a、b、c中不能组成直角三角形的是( )A、a=8,b=15,c=17 B、a=7,b=24,c=25 C、a=40,b=50,c=60 D、a= ,b=4,c=54. 在△ABC中,BC=5,AC=4,AB=3,则( )A、∠A=90° B、∠B=90° C、∠C=90° D、∠A+∠B=90°5. 2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的弦图,它是由四个全等的直角三角形和中间的小正方形拼成的一个大正方形,如图所示,如果大正方形的面积是34,小正方形的面积是4,直角三角形较短的直角边是a,较长的直角边是b,那么 的值为( )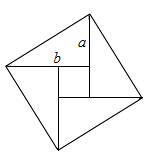 A、 38 B、49 C、52 D、646. 勾股定理在平面几何中有着不可替代的重要地位,在我国古算书(周髀算经》中就有“若勾三,股四,则弦五”的记载,如图1是由边长均为1的小正方形和Rt△ABC构成的,可以用其面积关系验证勾股定理,将图1按图2所示“嵌入”长方形LMJK,则该长方形的面积为( )
A、 38 B、49 C、52 D、646. 勾股定理在平面几何中有着不可替代的重要地位,在我国古算书(周髀算经》中就有“若勾三,股四,则弦五”的记载,如图1是由边长均为1的小正方形和Rt△ABC构成的,可以用其面积关系验证勾股定理,将图1按图2所示“嵌入”长方形LMJK,则该长方形的面积为( ) A、120 B、110 C、100 D、907. 如图,开口玻璃罐长、宽、高分别为16、6和6,在罐內点E处有一小块饼干碎末,此时一只蚂蚁正好在罐外长方形ABCD的中心H处,蚂蚁到达饼干的最短距离是多少( )
A、120 B、110 C、100 D、907. 如图,开口玻璃罐长、宽、高分别为16、6和6,在罐內点E处有一小块饼干碎末,此时一只蚂蚁正好在罐外长方形ABCD的中心H处,蚂蚁到达饼干的最短距离是多少( )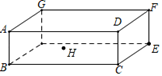 A、 B、17 C、 D、8. 如图,已知圆柱底面的周长为4 dm,圆柱的高为2 dm,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的周长的最小值为( )
A、 B、17 C、 D、8. 如图,已知圆柱底面的周长为4 dm,圆柱的高为2 dm,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的周长的最小值为( )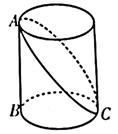 A、 dm B、 dm C、 dm D、 dm9. 如图,小巷左、右两侧是竖直的墙壁,一架梯子斜靠在左墙上时,梯子底端到左墙角的距离为1米,梯子顶端距离地面3米.若梯子底端位置保持不动,将梯子斜靠在右墙上,此时梯子顶端距离地面2米,则小巷的宽度为 ( )
A、 dm B、 dm C、 dm D、 dm9. 如图,小巷左、右两侧是竖直的墙壁,一架梯子斜靠在左墙上时,梯子底端到左墙角的距离为1米,梯子顶端距离地面3米.若梯子底端位置保持不动,将梯子斜靠在右墙上,此时梯子顶端距离地面2米,则小巷的宽度为 ( ) A、 米 B、3米 C、 米 D、2米10. 勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若图2中阴影部分的面积为2,且AB+AC=8,则BC的长为( )
A、 米 B、3米 C、 米 D、2米10. 勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若图2中阴影部分的面积为2,且AB+AC=8,则BC的长为( ) A、4 B、6 C、 D、
A、4 B、6 C、 D、二、填空题
-
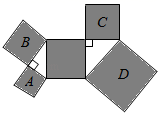
11. 若一个直角三角形的三边分别为x , 4,5,则x= .12. 如图,所有阴影四边形都是正方形,两个空白三角形均为直角三角形,且A、B、C三个正方形的边长分别为2、3、4,则正方形D的面积为.
 13. 如图,一棵大树在一次强台风中于离地面 处折断倒下,树干顶部在距离根部 处,这棵大树在折断前的高度为 .
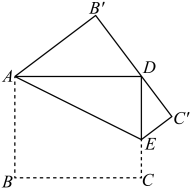
13. 如图,一棵大树在一次强台风中于离地面 处折断倒下,树干顶部在距离根部 处,这棵大树在折断前的高度为 .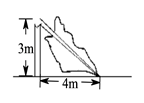 14. 如图,有一张长方形片ABCD , , .点E为CD上一点,将纸片沿AE折叠,BC的对应边 恰好经过点D,则线段DE的长为cm.
14. 如图,有一张长方形片ABCD , , .点E为CD上一点,将纸片沿AE折叠,BC的对应边 恰好经过点D,则线段DE的长为cm.
 15. 如图,在ΔABC中,AB=4,BC=2,DB=1,CD= ,则AC= .
15. 如图,在ΔABC中,AB=4,BC=2,DB=1,CD= ,则AC= .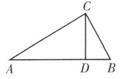 16. 没有上盖的圆柱盒高为10cm,周长为32cm,点A距离下底面3cm.一只位于圆柱盒外表面点A处的蚂蚁想爬到盒内表面对侧中点B处.则蚂蚁需要爬行的最短路程的长为cm.
16. 没有上盖的圆柱盒高为10cm,周长为32cm,点A距离下底面3cm.一只位于圆柱盒外表面点A处的蚂蚁想爬到盒内表面对侧中点B处.则蚂蚁需要爬行的最短路程的长为cm.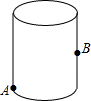 17. 我们学习了勾股定理后,都知道“勾三、股四、弦五”.
17. 我们学习了勾股定理后,都知道“勾三、股四、弦五”.观察:3、4、5;5、12、13;7、24、25;9、40、41;…,发现这些勾股数的勾都是奇数,且从3起就没有间断过.
(1)、请你根据上述的规律写出下一组勾股数:;(2)、若第一个数用字母n(n为奇数,且n≥3)表示,那么后两个数用含n的代数式分别表示为和 , 请用所学知识说明它们是一组勾股数.18. 如图,正方形 的边长为 ,其面积标记为 ,以 为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为 , 按照此规律继续下去,则 的值为.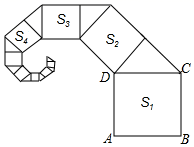
三、解答题
-
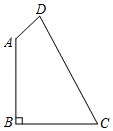
19. 如图,在四边形ABCD中,∠B=90°,AB=BC=2,AD=1,CD=3.求四边形ABCD的面积.
 20. 如图,小正方形的边长为1,△ABC的三个顶点都在小正方形的顶点处,判断△ABC的形状,并求出△ABC的面积.
20. 如图,小正方形的边长为1,△ABC的三个顶点都在小正方形的顶点处,判断△ABC的形状,并求出△ABC的面积.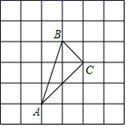
四、综合题
-
21. 如图:
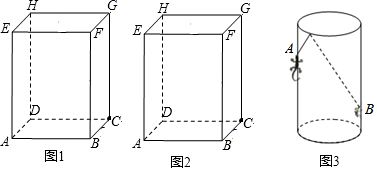 (1)、如图1,长方体的长为4cm,宽为3cm,高为12cm.求该长方体中能放入木棒的最大长度;(2)、如图2,长方体的长为4cm,宽为3cm,高为12cm.现有一只蚂蚁从点A处沿长方体的表面爬到点G处,求它爬行的最短路程.(3)、若将题中的长方体换成透明圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10cm,在容器内壁离底部3cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁且离容器上沿3cm的点A处.求蚂蚁吃到饭粒需要爬行的最短路程是多少?22. 如图,梯子长25米,斜靠在一面墙上,梯子底端离墙7米.
(1)、如图1,长方体的长为4cm,宽为3cm,高为12cm.求该长方体中能放入木棒的最大长度;(2)、如图2,长方体的长为4cm,宽为3cm,高为12cm.现有一只蚂蚁从点A处沿长方体的表面爬到点G处,求它爬行的最短路程.(3)、若将题中的长方体换成透明圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10cm,在容器内壁离底部3cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁且离容器上沿3cm的点A处.求蚂蚁吃到饭粒需要爬行的最短路程是多少?22. 如图,梯子长25米,斜靠在一面墙上,梯子底端离墙7米.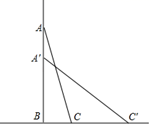 (1)、这个梯子的顶端距地面有多高?(2)、如果梯子的顶端下滑了4米,那么梯子的底端在水平方向滑动了几米?23. 王老师在一次“探究性学习”课中,设计了如下数表:
(1)、这个梯子的顶端距地面有多高?(2)、如果梯子的顶端下滑了4米,那么梯子的底端在水平方向滑动了几米?23. 王老师在一次“探究性学习”课中,设计了如下数表:n
2
3
4
5
…
a
22﹣1
32﹣1
42﹣1
52﹣1
…
b
4
6
8
10
…
c
22+1
32+1
42+1
52+1
…
(1)、请你分别观察a,b,c与n之间的关系,并用含自然数n(n>1)的代数式表示:a= , b= , c= .(2)、猜想:以a,b,c为边的三角形是否为直角三角形?并证明你的猜想?(3)、观察下列勾股数32+42=52 , 52+122=132 , 72+242=252 , 92+402=412 , 分析其中的规律,写出第五组勾股数 .24. 如图①,将两个边长为1的小正方形分别沿对角线剪开,拼成正方形ABCD.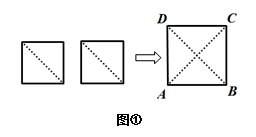
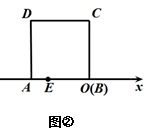 (1)、正方形ABCD的面积为 , 边长为 , 对角线BD=;(2)、求证: ;(3)、如图②,将正方形ABCD放在数轴上,使点B与原点O重合,边AB落在x轴的负半轴上,则点A所表示的数为 , 若点E所表示的数为整数,则点E所表示的数为25. 如图,已知△ABC中,∠B=90°,AB=8,CB=6,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.
(1)、正方形ABCD的面积为 , 边长为 , 对角线BD=;(2)、求证: ;(3)、如图②,将正方形ABCD放在数轴上,使点B与原点O重合,边AB落在x轴的负半轴上,则点A所表示的数为 , 若点E所表示的数为整数,则点E所表示的数为25. 如图,已知△ABC中,∠B=90°,AB=8,CB=6,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒. (1)、当t=2秒时,求PQ的长;(2)、求出发时间为几秒时,△PQB是等腰三角形?(3)、若Q沿B→C→A方向运动,则当点Q在边CA上运动时,求能使△BCQ成为等 腰三角形的运动时间。
(1)、当t=2秒时,求PQ的长;(2)、求出发时间为几秒时,△PQB是等腰三角形?(3)、若Q沿B→C→A方向运动,则当点Q在边CA上运动时,求能使△BCQ成为等 腰三角形的运动时间。