初中数学浙教版八年级上学期期中复习专题12 一元一次不等式组
试卷更新日期:2020-10-21 类型:复习试卷
一、单选题
-
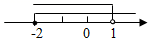
1. 不等式组 的解集在数轴上表示正确的是( )A、
 B、
B、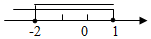 C、
C、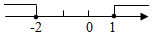 D、
D、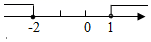 2. 不等式组 的解集是( )A、 B、 C、 D、3. 不等式组 的整数解共有( )A、1个 B、2个 C、3个 D、4个4. 关于x的不等式 的整数解只有4个,则m的取值范围是( )A、 B、 C、 D、5. 已知关于x的不等式组 ,无解,则a的取值范围是( )A、 ≤2 B、 ≥2 C、 <2 D、 >26. 某单位为响应政府号召,需要购买分类垃圾桶6个,市场上有A型和B型两种分类垃圾桶,A型分类垃圾桶500元/个,B型分类垃圾桶550元/个,总费用不超过3100元,则不同的购买方式有( )A、2种 B、3种 C、4种 D、5种7. 已知关于x、y的方程组 的解为整数,且关于x的不等式组 有且仅有5个整数解,则所有满足条件的整数a的和为( )A、﹣1 B、﹣2 C、﹣8 D、﹣68. 若关于x的不等式组 的解集为 ,则m的取值范围是( )A、m≥-2 B、m≤2 C、m <2 D、m=29. 若方程组 的解x,y满足 ,则k的取值范围是( )A、 B、 C、 D、10. 我们定义 ,例如: ,若 满足 ,则 的整数解有( )A、0个 B、1个 C、2个 D、3个
2. 不等式组 的解集是( )A、 B、 C、 D、3. 不等式组 的整数解共有( )A、1个 B、2个 C、3个 D、4个4. 关于x的不等式 的整数解只有4个,则m的取值范围是( )A、 B、 C、 D、5. 已知关于x的不等式组 ,无解,则a的取值范围是( )A、 ≤2 B、 ≥2 C、 <2 D、 >26. 某单位为响应政府号召,需要购买分类垃圾桶6个,市场上有A型和B型两种分类垃圾桶,A型分类垃圾桶500元/个,B型分类垃圾桶550元/个,总费用不超过3100元,则不同的购买方式有( )A、2种 B、3种 C、4种 D、5种7. 已知关于x、y的方程组 的解为整数,且关于x的不等式组 有且仅有5个整数解,则所有满足条件的整数a的和为( )A、﹣1 B、﹣2 C、﹣8 D、﹣68. 若关于x的不等式组 的解集为 ,则m的取值范围是( )A、m≥-2 B、m≤2 C、m <2 D、m=29. 若方程组 的解x,y满足 ,则k的取值范围是( )A、 B、 C、 D、10. 我们定义 ,例如: ,若 满足 ,则 的整数解有( )A、0个 B、1个 C、2个 D、3个二、填空题
-
11. 不等式组 的解集是 .12. 若关于x的一元一次不等式组 有2个整数解,则a的取值范围是 .13. 若不等式组 无解,则 a 的取值范围是.14. 若满足不等式 的最大整数解为a,最小整数解为b,则 的值为.15. 一件商品进价120元,标价a元,要按标价打6折销售,利润不会少于 ,标价a要满足.16. 我市认真落实国家“精准扶贫”政策,计划在对口帮扶的贫困县种植甲、乙两种火龙果共100亩,根据市场调查,甲、乙两种火龙果每亩的种植成本分别为0.9万元、1.1万元,每亩的销售额分别为2万元、2.5万元,如果要求种植成本不少于98万元,但不超过100万元,且所有火龙果能全部售出,则该县在此项目中获得的最大利润是万元.(利润=销售额﹣种植成本)17. 已知关于x的不等式组 有且只有2个整数解,且a为整数,则a的值为 .18. 不等式组 的解集为﹣1<x<1,则(a+2)(b﹣2)的值等于
三、解答题
-
19. 解不等式组: 并把解集在数轴上表示出来.
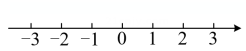 20. 已知不等式组 有且只有两个整数解,求实数a的取值范围,并用数轴把它表示出来.21. 求不等式组 的最小整数解.22. 某班有住校生若干人,若每个房间住4人,则剩下20人没有宿舍住;若每个房间住8人,则有一间宿舍住不满.求有多少间宿舍,多少名学生?23. 某单位计划在五一期间组织员工到某地旅游,参加旅游的人数估计为10至25人,甲、乙两家旅行社的服务质量相同,且报价都是每人200元.经过协商,甲旅行社表示可给予每位游客七五折优惠;乙旅行社表示可先免去一位游客的旅游费用,然后给予其余游客八折优惠.该单位选择哪一家旅行社支付的旅游费用较少?24. 新冠肺炎使得湖北的物资紧缺,为支援疫区,某村捐赠蔬菜30吨,水果13吨,现计划租用甲、乙两种货车共10辆将这批水果全部运往港口,已知一辆甲种货车可装蔬菜和水果共5吨,且一辆甲种货车可装的蔬菜重量(单位:吨)是其可装的水果重量的4倍,一辆乙种货车可装蔬菜水果各2吨;(1)、一辆甲种货车可装载蔬菜、水果各多少吨?(2)、该村安排甲、乙两种货车时有几种方案?请你帮助设计出来;(3)、若甲种货车每辆要付运输费2000元,乙种货车每辆要付运输费1500元,则该村应选择哪种方案?使运费最少?最少运费是多少元?25. 某农谷生态园响应国家发展有机农业政策,大力种植有机蔬菜,某超市看好甲、乙两种有机蔬菜的市场价值,经调查甲种蔬菜进价每千克m元,售价每千克16元;乙种蔬菜进价每千克n元,售价每千克18元.(1)、该超市购进甲种蔬菜15千克和乙种蔬菜20千克需要430元;购进甲种蔬菜10千克和乙种蔬菜8千克需要212元.求m,n的值.(2)、该超市决定每天购进甲、乙两种蔬菜共100千克,且投入资金不少于1160元又不多于1168元,设购买甲种蔬菜x千克,求有哪几种购买方案(3)、在(2)的条件下,超市在获得的利润取得最大值时,决定售出的甲种蔬菜每千克捐出 元,乙种蔬菜每千克捐出a元给当地福利院,若要保证捐款后的利润率不低于 ,求a的最大值.
20. 已知不等式组 有且只有两个整数解,求实数a的取值范围,并用数轴把它表示出来.21. 求不等式组 的最小整数解.22. 某班有住校生若干人,若每个房间住4人,则剩下20人没有宿舍住;若每个房间住8人,则有一间宿舍住不满.求有多少间宿舍,多少名学生?23. 某单位计划在五一期间组织员工到某地旅游,参加旅游的人数估计为10至25人,甲、乙两家旅行社的服务质量相同,且报价都是每人200元.经过协商,甲旅行社表示可给予每位游客七五折优惠;乙旅行社表示可先免去一位游客的旅游费用,然后给予其余游客八折优惠.该单位选择哪一家旅行社支付的旅游费用较少?24. 新冠肺炎使得湖北的物资紧缺,为支援疫区,某村捐赠蔬菜30吨,水果13吨,现计划租用甲、乙两种货车共10辆将这批水果全部运往港口,已知一辆甲种货车可装蔬菜和水果共5吨,且一辆甲种货车可装的蔬菜重量(单位:吨)是其可装的水果重量的4倍,一辆乙种货车可装蔬菜水果各2吨;(1)、一辆甲种货车可装载蔬菜、水果各多少吨?(2)、该村安排甲、乙两种货车时有几种方案?请你帮助设计出来;(3)、若甲种货车每辆要付运输费2000元,乙种货车每辆要付运输费1500元,则该村应选择哪种方案?使运费最少?最少运费是多少元?25. 某农谷生态园响应国家发展有机农业政策,大力种植有机蔬菜,某超市看好甲、乙两种有机蔬菜的市场价值,经调查甲种蔬菜进价每千克m元,售价每千克16元;乙种蔬菜进价每千克n元,售价每千克18元.(1)、该超市购进甲种蔬菜15千克和乙种蔬菜20千克需要430元;购进甲种蔬菜10千克和乙种蔬菜8千克需要212元.求m,n的值.(2)、该超市决定每天购进甲、乙两种蔬菜共100千克,且投入资金不少于1160元又不多于1168元,设购买甲种蔬菜x千克,求有哪几种购买方案(3)、在(2)的条件下,超市在获得的利润取得最大值时,决定售出的甲种蔬菜每千克捐出 元,乙种蔬菜每千克捐出a元给当地福利院,若要保证捐款后的利润率不低于 ,求a的最大值.