初中数学浙教版八年级上学期期中复习专题8 直角三角形的性质与判定
试卷更新日期:2020-10-21 类型:复习试卷
一、单选题
-
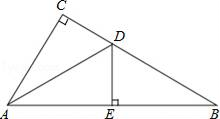
1. 如图,在Rt ABC中,∠ACB=90°,∠A=65°,CD⊥AB,垂足为D,E是BC的中点,连接ED,则∠EDC的度数是( )
 A、25° B、30° C、50° D、65°2. 如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=40°,那么∠2的度数是( )
A、25° B、30° C、50° D、65°2. 如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=40°,那么∠2的度数是( ) A、35° B、45° C、50° D、65°3. 在如图所示的网格纸中,有A,B两个格点,试取格点C,使得△ABC是直角三角形,则这样的格点C的个数是( )
A、35° B、45° C、50° D、65°3. 在如图所示的网格纸中,有A,B两个格点,试取格点C,使得△ABC是直角三角形,则这样的格点C的个数是( )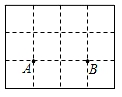 A、4 B、6 C、8 D、104. 如图, 是等边三角形, ,D是 的中点, 于点F, 于点E,则 的长是( )
A、4 B、6 C、8 D、104. 如图, 是等边三角形, ,D是 的中点, 于点F, 于点E,则 的长是( )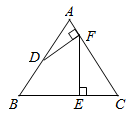 A、 B、 C、 D、35. 将一副三角尺按如图的方式摆放,其中l1∥l2 , 则∠α的度数是( )
A、 B、 C、 D、35. 将一副三角尺按如图的方式摆放,其中l1∥l2 , 则∠α的度数是( ) A、30° B、45° C、60° D、70°6. 如图,在△ABC中,∠C=90°,∠A=30°,AB的垂直平分线分别交AB、AC于点D、E,则以下AE与CE的数量关系正确的是( )
A、30° B、45° C、60° D、70°6. 如图,在△ABC中,∠C=90°,∠A=30°,AB的垂直平分线分别交AB、AC于点D、E,则以下AE与CE的数量关系正确的是( )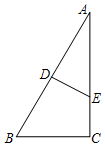 A、AE= CE B、AE= CE C、AE= CE D、AE=2CE7. 如图,在△ABC中,∠C=90°,点E是AC上的点,且∠1=∠2,DE垂直平分AB,垂足是D,如果EC=3cm,则AE等于( )
A、AE= CE B、AE= CE C、AE= CE D、AE=2CE7. 如图,在△ABC中,∠C=90°,点E是AC上的点,且∠1=∠2,DE垂直平分AB,垂足是D,如果EC=3cm,则AE等于( )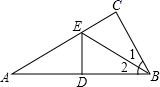 A、3cm B、4cm C、6cm D、9cm8. 如图,在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线交BC于点F,交AC于点E,交BA的延长线于点G.若EG=3,则BF=( )
A、3cm B、4cm C、6cm D、9cm8. 如图,在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线交BC于点F,交AC于点E,交BA的延长线于点G.若EG=3,则BF=( )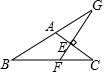 A、 B、3 C、2 D、49. 如图,在△ABC中,∠BAC=90°,∠ABC=2∠C,BE平分∠ABC交AC于E,AD⊥BE于D,下列结论:①AC-BE=AE;②点E在线段BC的垂直平分线上;③∠DAE=∠C;④BC=3AD,其中正确的个数有( )
A、 B、3 C、2 D、49. 如图,在△ABC中,∠BAC=90°,∠ABC=2∠C,BE平分∠ABC交AC于E,AD⊥BE于D,下列结论:①AC-BE=AE;②点E在线段BC的垂直平分线上;③∠DAE=∠C;④BC=3AD,其中正确的个数有( )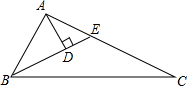 A、4个 B、3个 C、2个 D、1个10. 如图,在 中, , ,AD是 的中线,AE是 的角平分线, 交AE的延长线于点F,则DF的长是
A、4个 B、3个 C、2个 D、1个10. 如图,在 中, , ,AD是 的中线,AE是 的角平分线, 交AE的延长线于点F,则DF的长是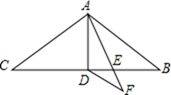 A、2 B、4 C、5 D、
A、2 B、4 C、5 D、二、填空题
-
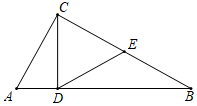
11. 如图,在△ABC中,∠ACB=90°,D,E分别为AB,AC上一点,将△BCD,△ADE分别沿CD,DE折叠,点A、B恰好重合于点A'处.若∠A'CA=18°,则∠AED=°.
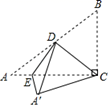 12. 如图,Rt△ABC中,∠ACB=90°,∠A=30°,点D是AB的中点,BC=2cm,则CD=cm.
12. 如图,Rt△ABC中,∠ACB=90°,∠A=30°,点D是AB的中点,BC=2cm,则CD=cm.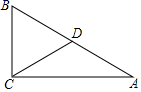 13. 已知 的周长是4+4 ,斜边上的中线长是2,则 .14. 如图,在△ABC中,∠ACB=90°,∠B=40°,D为线段AB的中点,则∠ACD= .
13. 已知 的周长是4+4 ,斜边上的中线长是2,则 .14. 如图,在△ABC中,∠ACB=90°,∠B=40°,D为线段AB的中点,则∠ACD= .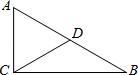 15. 如图,在△ABC中,∠C=90°,∠B=30°,AD平分∠CAB,交BC于点D,若CD=1,则BD=。
15. 如图,在△ABC中,∠C=90°,∠B=30°,AD平分∠CAB,交BC于点D,若CD=1,则BD=。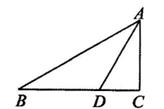 16. 如图,在 中, ,过点B作 ,交 于点D , 若 ,则 的长度为 .
16. 如图,在 中, ,过点B作 ,交 于点D , 若 ,则 的长度为 . 17. 如图,BD是∠ABC的角平分线,AD⊥BD,垂足为D,∠DAC=20°,∠C=38°,则∠BAD=.
17. 如图,BD是∠ABC的角平分线,AD⊥BD,垂足为D,∠DAC=20°,∠C=38°,则∠BAD=.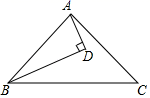 18. 如图,在等腰 中, , 为 边上的高, 分别为 边上的点,将 分别沿 折叠,使点 落在 的延长线上点 处,点 落在点 处,连接 ,若 ,则 的长是.
18. 如图,在等腰 中, , 为 边上的高, 分别为 边上的点,将 分别沿 折叠,使点 落在 的延长线上点 处,点 落在点 处,连接 ,若 ,则 的长是.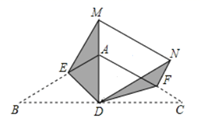
三、解答题
-
19. 如图,等腰△ABC,AB=AC,∠C=30°,AB⊥AD,AD=2,求BC的长.
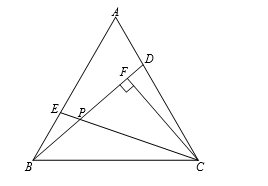
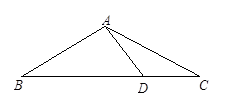 20. 如图,在锐角△ABC中,CD,BE分别是AB,AC边上的高,CD,BE交于点P,∠A=50°,求∠BPC的度数.
20. 如图,在锐角△ABC中,CD,BE分别是AB,AC边上的高,CD,BE交于点P,∠A=50°,求∠BPC的度数.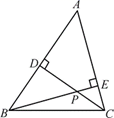 21. 已知:在△ABC中,∠B=30°,∠C=70°,AD⊥BC,AE是∠BAC的角平分线.
21. 已知:在△ABC中,∠B=30°,∠C=70°,AD⊥BC,AE是∠BAC的角平分线.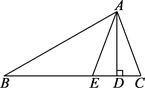 (1)、求∠EAC的度数;(2)、求∠EAD的度数.
(1)、求∠EAC的度数;(2)、求∠EAD的度数.