初中数学浙教版八年级上学期期中复习专题5 图形的轴对称
试卷更新日期：2020-10-21 类型：复习试卷
一、单选题
-
1. 下列图形不是轴对称图形的是（ ）A、
B、
C、
D、
2. 永州市教育部门高度重视校园安全教育，要求各级各类学校从认识安全警告标志入手开展安全教育．下列安全图标不是轴对称的是（ ）A、
B、
C、
D、
3. 下列图形是轴对称图形的是（ ）A、
B、
C、
D、
4. 下面四幅图是摄影爱好者抢拍的一组照片，从对称美的角度看，拍得最成功的是（ ）.A、
B、
C、
D、
5. 如图，在 中， ，垂足为D， 与 关于直线AD对称，点的B对称点是 ，则 的度数是（ ）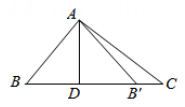
A、 B、 C、 D、6. 如图，直线MN是四边形AMBN的对称轴，与对角线交与点Q，点P是直线MN上任意一点，下列判断错误的是（ ）
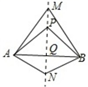A、AQ=BQ B、AP=BP C、∠MAP=∠MBP D、∠ANM=∠NMB7. 如图，弹性小球从点P出发，沿所示方向运动，每当小球碰到长方形的边时反弹，反弹时入射角等于反射角(即：∠1=∠2，∠3=∠4)．小球从P点出发第1次碰到长方形边上的点记为A点，第2次碰到长方形边上的点记为B点，……第2020次碰到长方形边上的点为图中的（ ）
A、A点 B、B点 C、C点 D、D点8. 如图，若△ABC与△DEF关于直线l对称，BE交l于点O ， 则下列说法不一定正确的是（ ）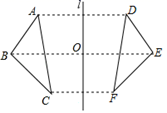
A、AB∥EF B、AC＝DF C、AD⊥l D、BO＝EO9. 如图， ， ，这个图形叫做“筝形”，数学兴趣小组几名同学探究出关于它的如下结论：① ；② ；③ ；④ ；⑤“筝形”是轴对称图形.其中正确的结论有（ ）
A、2个 B、3个 C、4个 D、5个10. 如图，在△ABC中，AC=BC，∠ACB=90°，点D在BC上，BD=6，DC=2，点P是AB上的动点，则PC+PD的最小值为（ ）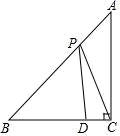
A、8 B、10 C、12 D、14二、填空题
-
11. 如图，在△ABC中，AB=AC，AD是BC边上的高，点E、F是AD的三等分点，若△ABC的面积为12，则图中△BEF的面积为。
12. 如图所示的五角星是轴对称图形，它的对称轴共有条．
13. 如图，3×3方格图中，将其中一个小方格的中心画上半径相等的圆，使整个图形为轴对称图形，这样的轴对称图形共有个。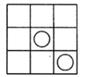
14. 如图，将△ABC沿着DE对折，点A落到A′处，若∠BDA′+∠CEA′＝70°，则∠A＝ ．
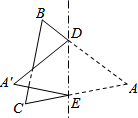15. 如图，在四边形ABCD中，∠BAD=130°，∠B=∠D=90°，点E，F分别是线段BC，DC上的动点．当△AEF的周长最小时，则∠EAF的度数为 ．
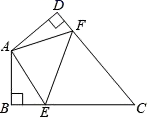16. 在 中，将 、 按如图所示方式折叠，点 、 均落于边 上一点 处，线段 、 为折痕．若 ，则 ．
17. 如图，等边△ABC的边长为2，过点B的直线 且△ABC与△A′BC′关于直线l对称，D为线段BC′上一动点，则AD+CD的最小值是.
18. 如图，等边△ 中， 于 ， ，点 、 分别为 、 上的两个定点且 ，在 上有一动点 使 最短，则 的最小值为 .
三、解答题
-
19. 如图，已知四边形ABCD和直线l，求作四边形ABCD以直线l为对称轴的对称图形A1B1C1D1 ．
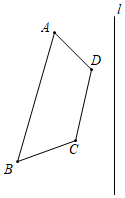20. 如图，△ABC和△ADE关于直线l对称，已知AB=15，DE=10，∠D=70°．求∠B的度数及BC、AD的长度
21. 在数学活动课上，王老师要求学生将图1所示的3×3正方形方格纸，剪掉其中两个方格，使之成为轴对称图形．规定：凡通过旋转能重合的图形视为同一种图形，如图2的四幅图就视为同一种设计方案（阴影部分为要剪掉部分）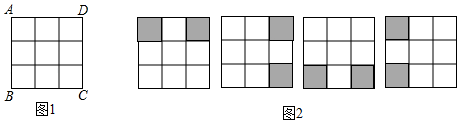
请在图中画出4种不同的设计方案，将每种方案中要剪掉的两个方格涂黑（每个3×3的正方形方格画一种，例图除外）
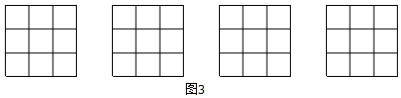22. 如图，点P是∠AOB内一点，分别作出P点关于OA、OB的对称点E、F，连接EF交OA于M，交OB于N，EF=15，求△PMN的周长．
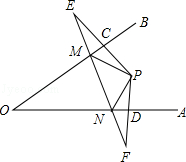23. 在等边△ABC中，点O在BC边上，点D在AC的延长线上，且OA=OD。
(1)、如图1，若点O为BC中点，求∠COD的度数；(2)、如图2，若点O为BC上的任意一点，求证：AD=AB+BO；(3)、如图3，若点O为BC上的任意一点，点D关于直线BC的对称点为点P，连接AP，OP，请判断△AOP的形状，并说明理由。24. 如图所示，在街道 的同一侧，有两个居民区A，B，两个居民区门口到街道的距离分别为AC，BD.现准备在街道 旁设置一个快递中转站.
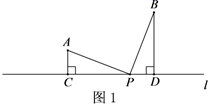
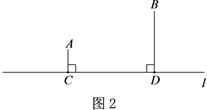
(1)、如果设置的快递中转站到A，B两个小区的距离相等，如图1，当∠A=∠BPD时，请说明AC+BD=CD的理由；(2)、如果设置的快递中转站到A，B两个小区的距离之和最短，请在图2中作出点P的位置，连接AP，BP，直接写出此时∠PAC与∠PBD的数量关系；(3)、为了能错峰进行取送快递，决定设置的快递中转站到A，B两个小区的距离之差最大，请在图3中作出点P的位置，连接AP，BP，直接写出此时∠PAC与∠PBD的数量关系.