初中数学浙教版八年级上学期期中复习专题3 全等三角形的性质与判定
试卷更新日期：2020-10-21 类型：复习试卷
一、单选题
-
1. 已知△ABC≌△DEF，点A与D，点C与F分别是对应点，则∠B的对应角是（ ）A、∠A B、∠F C、∠E D、∠C2. 如图，点E，点F在直线AC上， AE＝CF， AD＝CB，下列条件中不能判断△ADF≌△CBE的是（ ）
A、AD//BC B、BE//DF C、BE＝DF D、∠A＝∠C3. 如图，若△ABC≌△ADE，则下列结论中一定成立的是（ ）
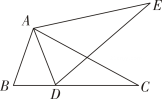A、AC＝DE B、∠BAD＝∠CAE C、AB＝AE D、∠ABC＝∠AED4. 如图，已知 ．能直接判断 的方法是（ ）
A、 B、 C、 D、5. 如图，等腰△ 中，点D ， E分别在腰AB ， AC上，添加下列条件，不能判定 ≌ 的是（ ）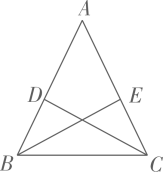
A、 B、 C、 D、6. △BDE和△FGH是两个全等的等边三角形，将它们按如图的方式放置在等边三角形ABC内.若求五边形DECHF的周长，则只需知道（ ）
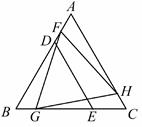A、△ABC的周长 B、△AFH的周长 C、四边形FBGH的周长 D、四边形ADEC的周长7. 如图，已知 和 都是等腰三角形， ， 交于点F，连接 ，下列结论：① ；② ；③ 平分 ；④ .其中正确结论的个数有（ ）
A、1个 B、2个 C、3个 D、4个8. 如图，锐角△ABC中，D，E分别是AB，AC边上的点，△ADC≌△ADC′，△AEB≌△AEB′，且C′D∥EB′∥BC，BE，CD交于点F．若∠BAC＝35°，则∠BFC的大小是（ ）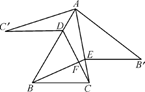
A、106° B、108° C、110° D、112°9. 如图，在 的网格中，每一个小正方形的边长都是1，点 ， ， ， 都在格点上，连接 ， 相交于 ，那么 的大小是（ ）
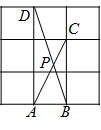A、 B、 C、 D、10. 如图，点P在∠MAN的角平分线上，点B，C分别在AM，AN上，作PR⊥AM，PS⊥AN，垂足分别是R，S．若∠ABP+∠ACP=180°，则下面三个结论：①AS=AR；②PC∥AB；③△BRP≌△CSP．其中正确的是（ ）
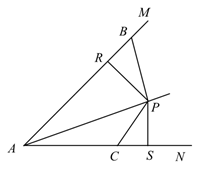A、①② B、②③ C、①③ D、①②③二、填空题
-
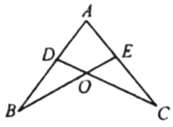
11. 如图，点D，E分别在线段AB，AC上，BE，CD相交于点O，AE = AD，要使△ABE≌△ACD，需添加一个条件是（只需一个即可，图中不能再添加其他点或线）.
12. 如图，在 和 中， ， ， ，则 º．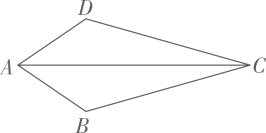
13. 如图，△ABC中，已知AB=5，AC=4，AD平分∠BAC交BC于D，DE⊥AC交AC于点E，若DE=2，则△ABC的面积为 ．
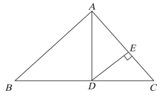14. 如图所示，在△ABC中，DM，EN分别垂直平分AB和AC，交BC于点D，E，若∠DAE=50°°，则∠BAC= ， 若△ADE的周长为19cm，则BC=cm.
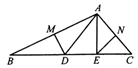15. 如图，已知AC与BF相交于点E ， AB∥CF ， 点E为BF中点，若CF=6，AD=4，则BD= ．
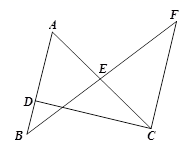16. 如图，点D、M、N分别为△AEB与△AFC的边与边的交点，AE⊥BE，AF⊥CF，垂足分别为E、F，AE=AF，BE=CF，则下列各个结论中：①∠EAF=90°；②CN=BM；③AN=BN；④△MCD≌△NBD．其中正确结论的序号为 ．
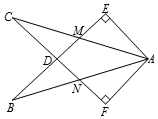17. 如图，点C在线段AB上，DA⊥AB ， EB⊥AB ， FC⊥AB ， 且DA＝ BC ， EB＝AC ， FC＝AB ， ∠AFB＝50°，则∠DFE＝ ．
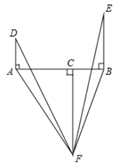18. 如图，△ABC中，∠ACB＝90°，AC＝BC，AE是BC边上的中线，过C作CF⊥AE，垂足为F，过B作BD⊥BC交CF的延长线于D，则下列结论：①若BD＝4，则AC＝8；②AB＝CD；③∠DBA＝∠ABC；④S△ABE＝S△ACE；⑤∠D＝∠AEC；⑥连接AD，则AD＝CD．其中正确的是 ． （填写序号）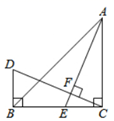
三、解答题
-
19. 如图，AB∥CD，AB=CD，CE=BF．请写出DF与AE的数量关系，并证明你的结论．
20. 如图，点D是AB上一点，DF交AC于点E，DE=FE，FC∥AB，AB=6，FC=4，求线段DB的长．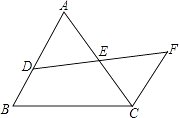
21. 如图在△ABC中，∠BAC=90°，AB=AC，AE是过点A的直线，CD⊥AE，BE⊥AE，若BE=2，CD=6，求DE的长度．
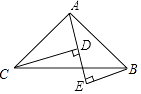22. 如图，∠C=∠D=90°，DA=CB，∠CBA=28°，求∠DAC．
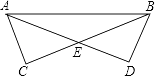23. 已知：AB＝AC ， AF＝AG ， AE⊥BG交BG的延长线于E ， AD⊥CF交CF的延长线于D ． 求证：AD＝AE ．
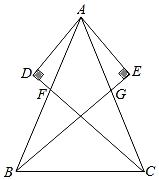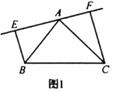
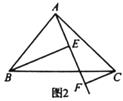
24. 如图，已知：△ABC中，AB=AC，∠BAC=90°，分别过B，C向经过点A的直线EF作垂线，垂足为E，F.
(1)、当EF与斜边BC不相交时，请证明EF=BE+CF（如图1）；(2)、如图2，当EF与斜边BC这样相交时，其他条件不变，证明：EF=BE－CF；(3)、如图3，当EF与斜边BC这样相交时，猜想EF、BE、CF之间的关系，不必证明.25. 如图1，在 中，∠BAC＝90°，点D为AC边上一点，连接BD，点E为BD点连接CE，∠CED＝∠ABD，过点A作AG⊥CE，垂足为G，AG交ED于点F．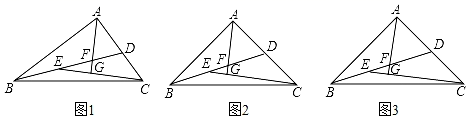
(1)、判断AF与AD的数量关系，并说明理由；(2)、如图2，若AC＝CE，点D为AC的中点，AB与AC相等吗？为什么？(3)、在（2）的条件下，如图3，若DF＝5，求 的面积．