初中数学浙教版八年级上学期期中复习专题2 定义与命题
试卷更新日期:2020-10-21 类型:复习试卷
一、单选题
-
1. 下列四个选项中不是命题的是( )A、对顶角相等 B、过直线外一点作直线的平行线 C、三角形任意两边之和大于第三边 D、如果 ,那么2. 下列关于命题“若 ,则 ”的说法,正确的是( )A、是真命题 B、是假命题,反例是“ ” C、是假命题,反例是“ ” D、是假命题,反例是“ ”3. 下列命题中,是真命题的是( ) .A、两条直线被第三条直线所截,同位角相等 B、一个角的余角必为锐角,一个角的补角不一定为钝角 C、相等的两个角是对顶角 D、从直线外一点到这条直线的垂线段,叫做这点到直线的距离4. 下列命题中,是真命题的是( )A、内错角相等 B、邻补角相等 C、同旁内角相等两直线平行 D、平行于同一直线的两直线平行5. 下列命题中,假命题是( )A、直角三角形的两个锐角互余 B、三角形的外角和等于360° C、同位角相等 D、三角形的任意两边之差小于第三边6. 若命题“ ”不成立,那么a与0的大小关系是( )A、 B、 C、 D、7. 下列语句中,是命题的是( )
①若∠1=60°,∠2=60°,则∠1=∠2;②同位角相等吗?③画线段AB=CD;④如果a>b,b>c,那么a>c;⑤直角都相等.
A、①④⑤ B、①②④ C、①②⑤ D、②③④⑤8. 我们知道“对于实数m,n,k,若m=n,n=k,则m=k”,即相等关系具有传递性.小敏由此进行联想,提出了下列命题:①a,b,c是直线,若a∥b,b∥c,则a∥c.
②a,b,c是直线,若a⊥b,b⊥c,则a⊥c.
③若∠α与∠β互余,∠β与∠γ互余,则∠α与∠γ互余.
其中正确的命题是( )
A、① B、①② C、②③ D、①②③9. 下列语句中,不是命题的是( )A、两点确定一条直线 B、垂线段最短 C、作角A的平分线 D、内错角相等10. 下列命题中:①等腰三角形底边的中点到两腰的距离相等;②等腰三角形的高、中线、角平分线互相重合;③若△ABC与△DEF成轴对称,则△ABC一定与△DEF全等;④有一个角是60度的三角形是等边三角形;⑤等腰三角形的对称轴是顶角的平分线.正确命题的个数是( )A、2 B、3 C、4 D、5二、填空题
-
11. 用一组a,b的值说明命题“如果 ,那么 ”是错误的,这组值可以是.12. 有下列命题:①无理数是无限不循环小数;②平方根与立方根相等的数有1和0;③若a⊥b,b⊥c,则a⊥c;④邻补角是互补的角;⑤无理数包括正无理数、零、负无理数.其中正确的有个.13. 命题“如果x2=y2”,那么“x=y”是命题(填“真”成“假”).14. 将命题“互为余角的两个角之和等于90°”,改写成“如果…那么…”的形式是:.15. 写出命题“如果a=b”,那么“3a=3b”的逆命题 .
16. 命题“两直线平行,同位角相等”的题设是;结论是.17. 对于命题“如果∠1+∠2=90°,那么∠1=∠2”,能说明它是假命题的反例是.18. 阅读下列语句:①对顶角不相等;②邻补角是互补的角;③同位角相等;④画∠AOB的平分线OC;⑤这个角等于30°吗?在这些语句是,属于命题的是(填写序号).
三、解答题
-
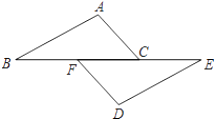
19. 下列各命题的条件是什么?结论是什么?(1)、两直线平行,同位角相等;(2)、过一点有且只有一条直线与已知直线平行.20. 下列语句哪些是命题?对于命题,请先将它改写为“如果……那么……”的形式,再找出命题的条件和结论,并指出是真命题还是假命题,并说明为什么是假命题.(1)、小亮今年上八年级,明年一定上九年级;(2)、作一条线段的垂直平分线;(3)、互为倒数的两个数的积为1;(4)、内错角相等;(5)、不等式的两边同时乘以一个数,不等号的方向改变.21. 判断下列命题是真命题还是假命题,如果是假命题,请举出一个反例.(1)、如果一个数是偶数,那么这个数是4的倍数.(2)、两个负数的差一定是负数.22. 对于同一平面内的三条直线a,b,c,给出下列5个判断:①a∥b,②b∥c③a⊥b④a∥c⑤a⊥c,请以其中两个论断为条件,一个论断为结论,组成一个你认为正确的命题(至少写三个命题)23. 已知命题:若a > b , 则a 2 > b 2 .(1)、此命题是真命题还是假命题?若是真命题,请给予证明;若是假命题,请举出一个反例;(2)、若结论保持不变,那么怎样改变条件,命题才能正确?(3)、若条件保持不变,那么怎样改变结论,命题才能正确?24. 已知命题:“如图,点B、F、C、E在同一条直线上,则AB∥DE.”判断这个命题是真命题还是假命题,如果是真命题,请给出证明;如果是假命题,在不添加其他辅助线的情况下,请添加一个适当的条件使它成为真命题,并加以证明.