初中数学浙教版八年级上学期期中复习专题1 三角形的边和角

试卷更新日期：2020-10-21 类型：复习试卷

进入出卷网下载

一、单选题

1. 以下列各组长度的线段为边，能构成三角形的是（）

A、7，3，4 B、5，6，12 C、3，4，5 D、1，2，3

查看试题解析
2. 若一等腰三角形的腰长为4 cm，腰上的高为2 cm，则等腰三角形的顶角为（）

A、30° B、150° C、30°或150° D、以上都不对

查看试题解析
3. 在下列条件中:①∠A+∠B=∠C，②∠A:∠B:∠C=1:2:3，③∠A = 90°－∠B，④∠A = ∠B-∠C中，能确定△ABC是直角三角形的条件有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
4. 下列线段，不能做成直角三角形的是（）

A、 $\frac{1}{3}$ cm， $\frac{1}{4}$ cm， $\frac{1}{5}$ cm B、3cm，4cm，5cm C、7cm，24cm，25cm D、10cm，24cm，26cm

查看试题解析
5. 如图，把△ABC纸片沿DE折叠，当点A落在四边形BCDE内部时，则∠A与∠1+∠2之间有一种数量关系始终保持不变.请试着找一找这个规律，你发现的规律是（）

A、∠A=∠1+∠2 B、2∠A=∠1+∠2 C、3∠A=2∠1+∠2 D、3∠A=2（∠1+∠2）

查看试题解析
6. 如图，已知∠AOB＝10°，且OC＝CD＝DE＝EF＝FG＝GH，则∠BGH＝（）

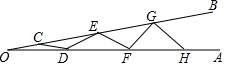A、50° B、60° C、70° D、80°

查看试题解析
7. 如图，在△ABC中，AD，BE分别是BC，AC边上的中线，且AD⊥BE，垂足为点F，设BC＝a，AC＝b，AB＝c，则下列关系式中成立的是（）

A、a²+b²＝5c² B、a²+b²＝4c² C、a²+b²＝3c² D、a²+b²＝2c²

查看试题解析
8. 如图， $△ O A_{1} A_{2}$ 为等腰直角三角形，OA₁＝1，以斜边OA₂为直角边作等腰直角三角形OA₂A₃ ，再以OA₃为直角边作等腰直角三角形OA₃A₄ ， …，按此规律作下去，则OA_n的长度为（）

A、（ $\sqrt{2}$ ）ⁿ B、（ $\sqrt{2}$ ）ⁿ^﹣¹ C、（ $\frac{\sqrt{2}}{2}$ ）ⁿ D、（ $\frac{\sqrt{2}}{2}$ ）ⁿ^﹣¹

查看试题解析
9. 将一副三角尺按如图所示的方式摆放，则 $∠ α$ 的大小为（）

A、 $85 °$ B、 $75 °$ C、 $65 °$ D、 $60 °$

查看试题解析
10. 如图，在△ABC中，AC=AB，∠BAC=90°，BD平分∠ABC，与AC相交于点F，CD⊥BD，垂足为D，交BA的延长线于点E，AH⊥BC交BD于点M，交BC于点H，下列选项不正确的是（）

A、∠E＝67.5° B、∠AMF＝∠AFM C、BF＝2CD D、BD＝AB+AF

查看试题解析

二、填空题

11. 如图，AB∥CD，∠1=50°，∠2=110°，则∠3=

查看试题解析
12. 等腰三角形的腰长为17，底长为16，则其底边上的高为.

查看试题解析
13. 在等腰 $△$ ABC中，AB＝AC，∠B＝50°，则∠A的大小为．

查看试题解析
14. 已知：如图，在△ABC中，点D，E，F分别在三边上，E是AC的中点，BD＝2DC，AD，BE，CF交于一点G，S_△_BGD＝16，S_△_AGE＝6，则△ABC的面积是.

查看试题解析
15. 已知三角形的两边长分别为3和6，则这个三角形的第三边长可以是(写出一个即可)，

查看试题解析
16. 如图， $A C$ 平分 $∠ D C B$ ， $C B = C D$ ， $D A$ 的延长线交 $B C$ 于点E，若 $∠ E A C = 49^{\circ}$ ，则 $∠ B A E$ 的度数为．

查看试题解析
17. 如图，在 $△ A B C$ 中， $B C$ 的垂直平分线分别交 $B C$ 、 $A B$ 于点E、F.若 $△ A F C$ 是等边三角形，则 $∠ B =$ °.

查看试题解析
18. 将一副三角板如图放置，则图中的∠1＝°.

查看试题解析

三、解答题

19. 如图，在 $△ A B C$ . $A E$ 是 $∠ B A C$ 的平分线， $A D$ 是 $B C$ 边上的高， $∠ B A C = 80 °$ ， $∠ E A D = 15 °$ ，求 $∠ B$ 的度数．

查看试题解析
20. 如图，在 $△ A B C$ 中， $A B = A C$ ，点 $D$ 在边 $B C$ 上，且 $B D = A B$ ，连接 $A D$ ，若 $A D = C D$ ，求 $∠ B$ 的度数．

查看试题解析
21. 已知 $Δ A B C$ 的三边长分别为 $a$ ， $b$ ， $c$ ，化简 $| a + b - c | + | b - a - c |$ .

查看试题解析
22. 如图，在△ABC中，AB=AC，AD⊥BC于点D.

(1)、若∠C=42°，求∠BAD的度数；

(2)、若点E在边AB上，EF∥AC交AD的延长线于点F.
求证：AE=FE.

查看试题解析
23. 如图1，在△ABC中，AB＝AC，点D是BC的中点，点E在AD上.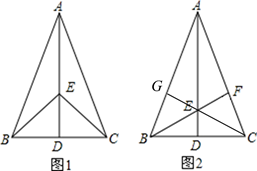

(1)、求证：∠ABE＝∠ACE；

(2)、如图2，若BE的延长线交AC于点F，CE的延长线交AB于点G.求证：EF＝EG.

查看试题解析
24. 如图

(1)、如图（1），已知CE与AB交于点E，AC=BC，∠1=∠2.求证： $△ A C E ≅ △ B C E$ .

(2)、如图（2），已知CD的延长线与AB交于点E，AD=BC，∠3=∠4.探究AE与BE的数量关系，并说明理由.

查看试题解析
25. 如图，点P、Q分别是等边 $Δ A B C$ 边AB、BC上的动点（端点除外），点P、点Q以相同的速度，同时从点A、点B出发．

(1)、如图1，连接AQ、CP求证： $Δ A B Q ≅ Δ C A P$

(2)、如图1，当点P、Q分别在AB、BC边上运动时，AQ、CP相交于点M， $∠ Q M C$ 的大小是否变化？若变化，请说明理由；若不变，求出它的度数

(3)、如图2，当点P、Q在AB、BC的延长线上运动时，直线AQ、CP相交于M， $∠ Q M C$ 的大小是否变化？若变化，请说明理由；若不变，求出它的度数．

查看试题解析