浙江省温州市鹿城区2020届九年级上学期数学第一次月考试卷
试卷更新日期：2020-10-20 类型：月考试卷
一、选择题（本大题共10小题，共30分）
-
1. 下列四个圆形图案中，分别以它们所在圆的圆心为旋转中心，顺时针旋转120°后，能与原图形完全重合的是（ ）A、
B、
C、
D、
2. 已知点P在半径为5cm的圆内，则点P到圆心的距离可以是A、4cm B、5cm C、6cm D、7cm3. 将抛物线y= x2向右平移2个单位所得抛物线的函数表达式为（ ）A、y =(x-2)2 B、y=（x+2）2 C、y=x2 - 2 D、y =x 2+ 24. 已知一个二次函数y = ax2（a≠0）的图象经过（－2，8），则下列点中在该函数的图象上的是（ ）A、（2，8） B、（1，3） C、（ －1，3） D、（2，6）5. 如图，AB是⊙O的直径，点C、D在⊙O上，∠BOC = 110°，AD∥OC，则∠AOD = （ ）
A、70° B、60° C、50° D、40°6. 设A（－2，y1），B（1，y2），C（2，y3）是抛物线y =-（x+1）2 + 3上的三点，则y1 ， y2 ， y3的大小关系为（ ）A、y1 > y2 > y3 B、y1> y3 > y2 C、y3 > y2 > y1 D、y3>y1>y27. 如图是我市环北路改造后一圆柱形输水管的横截面，阴影部分为有水部分，如果水面AB宽为4m，水面最深地方的高度为1m，则该输水管的半径为（ ）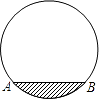
A、2m B、2.5m C、4m D、5m8. 如图，已知抛物线 的顶点为（2，-1），抛物线与y轴的交点为（0，3），当函数值 时，自变量x的取值范围是（ ）
A、 B、 C、 D、9. 如图，某隧道美化施工，横截面形状为抛物线y =－ x2 + 8（单位：米），施工队计划在隧道正中搭建一个矩形脚手架DEFG，已知DE：EF = 3：2，则脚手架高DE为（ ）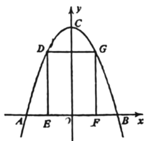
A、7米 B、6.3米 C、6米 D、5米10. 如图，AB为⊙O的直径，点D是弧AC的中点，过点D作DE⊥AB于点E，延长DE交⊙OO于点F，若AC = 12，AE = 3，则⊙O的直径长为（ ）
A、10 B、13 C、15 D、16二、填空题（本大题共8小题，共24分）
-
11. 抛物线y =- （x-4）2 + 3的顶点坐标是 ；12.
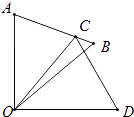
如图，△COD是△AOB绕点O顺时针旋转40°后得到的图形，若点C恰好落在AB上，且∠AOD的度数为90°，则∠B的度数是 ．
13. 抛物线y=ax2 + bx + c上部分点的横坐标x纵坐标y的对应值如下表:x
…
-3
-2
-1
0
1
…
y
…
-6
0
4
6
6
…
容易看出，（ - 2，0）是抛物线与x的一个交点，则它与x轴的另一个交点的坐标为
14. 如下图，已知AB是⊙O的直径， ，∠BOC = 40°，那么∠AOE等于 .
15. 若圆的半径为6 cm，圆中一条弦长为6 cm，则此弦中点到此弦所对弧的中点的距离为 cm；16. 如图，公园里喷水池中的水柱的形状可以看成是抛物线，小明想知道水柱的最大高度，于是画出示意图，并测出了一些数据：水柱上的点C，D到地面的距离都是1.6米，即BC = OD = 1.6米，AB = 1米，AO = 5米，则水柱的最大高米.
17. 如图，是一个半圆和抛物线的一部分围成的“芒果”，已知点A，B，C，D分别是“芒果”与坐标轴的交点，AB是半圆的直径，抛物线的解析式为y = x2－ ，则图中CD的长为 .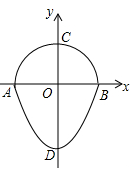
18. 如图，在平行四边形ABCD中，∠A = 45°，AB = 6，AD = 2 ，M是AD边的中点，N是AB边上的一动点，将△AMN沿MN所在直线翻折得到△A′MN，连接A′C，则A′C长度的最小值是 .
三、解答题（本大题共6小题，共46分）
-
19.
(1)、尺规作图：作△ABC的外接圆⊙O.（保留作图痕迹，不写画法）(2)、若∠A = 45°，⊙O的半径为1，求BC的度数和BC的长.20. 如图，A、B、C、D是⊙O上四点，且AB = CD，求证：AD = BC.
21. 如图，抛物线y = x2 - bx + 3与x轴相交于点A，B，且过点C（4，3）
(1)、求b的值和该抛物线顶点P的坐标；(2)、将该抛物线向左平移，记平移后抛物线的顶点为P’，当四边形AP’PB为平行四边形时，求平移后抛物线的解析式22. 如图，D是⊙O弦BC的中点，A是上一点，OA与BC交于点E，已知AO = 8，BC = 12.
(1)、求线段OD的长.(2)、当EO = BE时，求ED，EO的长.23. 某养鸡专业户用篱笆及一面墙（该墙可用最大长度为36米）围成一个矩形场地ABCD来供鸡室外活动，该场地中间隔有一道与AB平行的篱笆（EF），如图，BE、EF上各留有1米宽的门（门不需要篱笆），该养鸡专业户共用篱笆58米，设该矩形的一边AB长x米，AD > AB，矩形ABCD的面积为s平方米.
(1)、求出S与x的函数关系式，直接写出自变量x的取值范围：(2)、若矩形ABCD的面积为252平方米，求AB的长.(3)、若规定AB≥10米，则矩形ABCD面积的最大值是多少?24. 如图，已知抛物线y =－x 2+ bx + c与x轴正半轴交于点A（3，0），与y轴交于点B（0，3），点P是x轴上一动点，过点P作x轴的垂线交抛物线于点C，交直线AB于点D，设P（x，0）.
(1)、求抛物线的函数表达式：(2)、当0 < x < 3时，求线段CD的最大值；(3)、若P点在x正半轴移动时，在△PDB和△CDB中，当其中一个三角形的面积是另一个三角形面积的2倍时，求相应x的值：(4)、若点Q在抛物线上，点H在线段AB的垂直平分线上，且点Q，H，A，B为顶点的四边形是平行四边形，求Q点的横坐标.