浙江省台州市书生（双语）2021届九年级数学上学期第一次月考试卷

试卷更新日期：2020-10-20 类型：月考试卷

进入出卷网下载

一、选择题（本题共10小题，每题4分，共40分）

1. 观察下列图形，其中既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下随有关圆的一些结论：①任意三点确定一个圆；②相等的圆心角所对的弧相等；③平分弦的直径垂直于弦；并且平分弦所对的弧，④圆内接四边形对角互补．其中错误的结论有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 已知⊙O的半径r=3，PO= $\sqrt{10}$ ，则点P与⊙O的位置关系是( )

A、点P在⊙O内 B、点P在⊙O上 C、点P在⊙O外 D、不能确定

查看试题解析
4.
数学课上，老师让学生尺规作图画Rt△ABC，使其斜边AB=c，一条直角边BC=a，小明的作法如图所示，你认为这种作法中判断∠ACB是直角的依据是（　　）

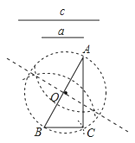A、勾股定理 B、勾股定理是逆定理 C、直径所对的圆周角是直角 D、90°的圆周角所对的弦是直径

查看试题解析
5. 如图， $A B$ 是 $⊙ O$ 的弦， $O C ⊥ A B$ 交 $⊙ O$ 于点 $C$ ，点 $D$ 是 $⊙ O$ 上一点， $∠ A D C = 30 °$ ，则 $∠ B O C$ 的度数为（）．

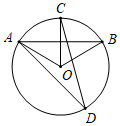A、30° B、40° C、50° D、60°

查看试题解析
6. 如图，AB，AC，BD是⊙O的切线，切点分别是P，C，D.若AC=5，BD=3，则AB的长是（　　）

A、2 B、4 C、6 D、8

查看试题解析
7. 以坐标原点O为圆心，作半径为2的圆，若直线y=-x+b与⊙O相交，则b的取值范围是（　　）

A、 $0 \leq b \leq 2 \sqrt{2}$ B、 $- 2 \sqrt{2} < b < 2 \sqrt{2}$ C、 $- 2 \sqrt{3} \leq b \leq 2 \sqrt{3}$ D、 $- 2 \sqrt{2} \leq b \leq 2 \sqrt{2}$

查看试题解析
8. 如图，在平面直角坐标系中，过格点A，B，C作一圆弧，点B与下列格点的连线中，能够与该圆弧相切的是（）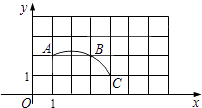

A、点（0，3） B、点（2，3） C、点（5，1） D、点（6，1）

查看试题解析
9. 如图，将矩形ABCD绕点A旋转至矩形AEFG的位置，此时点D恰好与AF的中点重合，AE交CD于点H，若BC=2 $\sqrt{3}$ ，则HC的长为（　　）

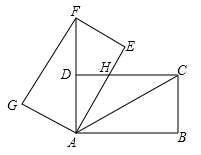A、4 B、2 $\sqrt{3}$ C、3 $\sqrt{3}$ D、6

查看试题解析
10. 如图，已知直线y= $\frac{5}{12} x - 5$ 与x轴、y轴分别交于B、C两点，A是以D（0，2）为圆心，2为半径的圆上一动点，连结AC、AB，则△ABC面积的最小值是（　　）

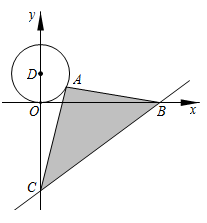A、30 B、29 C、28 D、27

查看试题解析

二、填空题（本题共6小题，每题5分，共30分）

11. 如图，圆拱桥的拱顶到水面的距离CD为9m，水面宽AB为6m，则桥拱半径OC为m.

查看试题解析
12. 如图，在△ABC中，AB=BC，将△ABC绕点B顺时针旋转α度，得到△A₁BC₁ ， A₁B交AC于点E，A₁C₁分别交AC，BC于点D，F，下列结论：①∠CDF=α，②A₁E=CF，③DF=FC，④AD=CE，⑤A₁F=CE.其中正确的是（写出正确结论的序号）

查看试题解析
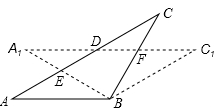13. 如图，点A，B，C，D都在⊙O上，弧CD 的度数等于84°，CA是∠OCD的平分线，则∠ABD+∠CAO=°

查看试题解析
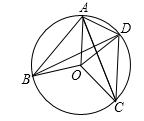14. 如图，△ABC内接于⊙O，∠CAB=30°，∠CBA=45°，CD⊥AB于点D，若⊙O的半径为2，则CD的长为。

查看试题解析
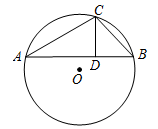15. 如图，在平面直角坐标系中，已知点A （0，1）、B（0，1+t）、C（0，1-t）（t＞0），点P在以D（4，4）为圆心，1为半径的圆上运动，且始终满足∠BPC=90°，则t的取值范围是。

查看试题解析
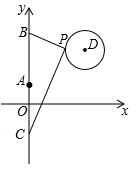16. 问题背景：如图1，将△ABC绕点A逆时针旋转60°得到△ADE，DE与BC交于点P，可推出结论：PA+PC=PE.问题解决：如图2，在△MNG中，MN=6，∠M=75°，MG=4 $\sqrt{2}$ 。点O是△MNG内一点，则点O到△MNG三个顶点的距离和的最小值是。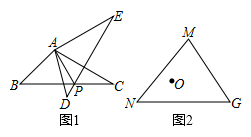

查看试题解析

三、解答题（本题共8小题，第17~20每题8分，第21题10分，第22、23题每题12分，第24题14分，共80分）

17. 将两块大小相同的含30°角的直角三角板（∠BAC=∠B′A′C=30°）按图①方式放置，固定三角板A′B′C，然后将三角板ABC绕直角顶点C顺时针方向旋转（旋转角小于90°）至图②所示的位置，AB与A′C交于点E，AC与A′B′交于点F，AB与A′B′相交于点O.

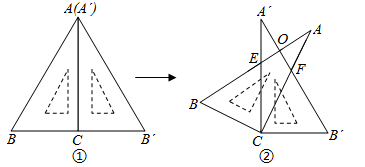(1)、求证：△BCE≌△B′CF；

(2)、当旋转角等于30°时，AB与A′B′垂直吗？请说明理由.

查看试题解析
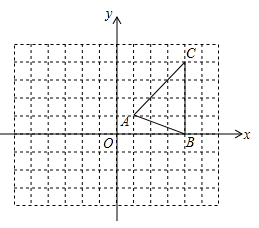
18. 如图，以点O为圆心的两个同心圆中，矩形ABCD的边BC为大圆的弦，边AD与小圆相切于点M，OM的延长线与BC相交于点N．

(1)、点N是线段BC的中点吗？为什么？

(2)、若圆环的宽度（两圆半径之差）为6cm，AB=5cm，BC=10cm，求小圆的半径．

查看试题解析
19. 如图，在平面直角坐标系xOy中，△ABC的三个顶点坐标分别为A（1，1），B（4，0），C（4，4）
按下列要求作图：
①将△ABC向左平移4个单位，得到△A₁B₁C₁ ，并写出A₁ ， B₁ ， C₁的坐标。

②将△A₁B₁C₁绕点B₁逆时针旋转90°，得到△A₂B₂C₂；并写出A₂ ， C₂的坐标。

查看试题解析
20. 已知PA，PB分别与⊙O相切于点A，B，∠APB=80°，C为⊙O上一点.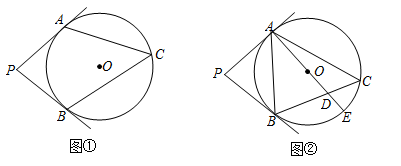

(1)、如图①，求∠ACB的大小；

(2)、如图②，AE为⊙O的直径，AE与BC相交于点D.若AB=AD，求∠EAC的大小.

查看试题解析
21. 如图，A、B是⊙O上的两点，∠AOB=120°，点D为劣弧AB 的中点.

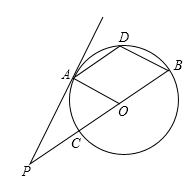(1)、求证：四边形AOBD是菱形；

(2)、延长线段BO至点P，交⊙O于另一点C，且BP=3OB，求证：AP是⊙O的切线

查看试题解析
22. 已知P是⊙O上一点，过点P作不过圆心的弦PQ，在劣弧PQ和优弧PQ上分别有动点A、B（不与P，Q重合），连接AP、BP.若∠APQ=∠BPQ.

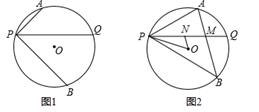(1)、如图1，当∠APQ=45°，AP=1，BP=2 $\sqrt{2}$ 时，求⊙O的半径；

(2)、如图2，连接AB，交PQ于点M，点N在线段PM上（不与P、M重合），连接ON、OP，若∠NOP+2∠OPN=90°，探究直线AB与ON的位置关系，并证明.

查看试题解析
23. 阅读材料：
在平面直角坐标系xOy中，点P（x0，y0）到直线Ax+By+C=0的距离公式为： $d = \frac{| A x_{0} + B x_{0} + C |}{\sqrt{A^{2} + B^{2}}}$ .

例如：求点P₀（0，0）到直线4x+3y-3=0的距离.

解：由直线4x+3y-3=0知，A=4，B=3，C=-3，

∴点P₀（0，0）到直线4x+3y-3=0的距离为 $d = \frac{| 4 \times 0 + 3 \times 0 - 3 |}{\sqrt{4^{2} + 3^{2}}} = \frac{3}{5}$

根据以上材料，解决下列问题：

(1)、问题1：点P₁（3，4）到直线 $y = - \frac{3}{4} x + \frac{5}{4}$ 的距离为；

(2)、问题2：已知：⊙C是以点C（2，1）为圆心，1为半径的圆，⊙C与直线 $y = - \frac{3}{4} x + b$ b相切，求实数b的值；

(3)、问题3：如图，设点P为问题2中⊙C上的任意一点，点A，B为直线3x+4y+5=0上的两点，且AB=2，请求出S_△ABP的最大值和最小值.

查看试题解析
24. 我们知道：有一内角为直角的三角形叫做直角三角形.类似地，我们定义：有一内角为45°的三角形叫做半直角三角形.如图，在平面直角坐标系中，O为原点，A（2，0），B（-2，0），D是y轴上的一个动点，∠ADC=90°（A、D、C按顺时针方向排列），BC与经过A、B、D三点的⊙M交于点E，DE平分∠ADC，连结AE，BD.显然△DCE、△DEF、△DAE是半直角三角形.

(1)、求证：△ABC是半直角三角形；

(2)、求证：∠DEC=∠DEA；

(3)、若点D的坐标为（0，8），求AE的长；

(4)、BC交y轴于点N，问 $\frac{C N}{O D}$ 的值是否发生变化？若不发生变化，请求出其值；若发生变化，请说明理由。

查看试题解析