浙江省温州市2021届九年级上学期数学第一次月考试卷
试卷更新日期：2020-10-20 类型：月考试卷
一、选择题（本题共有10小题，每小题4分，共40分．请选出各题中一个符合题意的正确选项，不选，多选，错选，均不得分）
-
1. 在下列函数中，属于二次函数的是（ ）A、y= B、 C、y= D、y=3x-52. “a是实数，
”这一事件是 （ ） A、必然事件 B、不确定事件 C、不可能事件 D、随机事件3. 对于抛物线y=-（x-5）2+3，下列说法正确的是（ ）
A、开口向下，顶点坐标（5，3） B、开口向上，顶点坐标（5，3） C、开口向下，顶点坐标（-5，3） D、开口向上，顶点坐标（-5，3）4. 在一个不透明的口袋中装有5个完全相同的小球，把它们分别标号为1，2，3，4，5，从中随机摸出一个小球，其标号大于2的概率为（ ）A、 B、 C、 D、5. 要得到 y=-2(x+2)2-3 的图象,需将抛物线y=－2x2作如下平移（ ）A、向右平移2个单位,再向上平移3个单位 B、向右平移2个单位,再向下平移3个单位 C、向左平移2个单位,再向上平移3个单位 D、向左平移2个单位,再向下平移3个单位6. 从n个苹果和3个雪梨中，任选1个，若选中苹果的概率是 ，则n的值是（ ）A、6 B、3 C、2 D、17. 下列函数中函数值有最大值的是（ ）A、y= B、y=- C、y=-x2 D、y=x2-28. 一个袋中里有4个珠子，其中2个红色，2个蓝色，除颜色外其余特征均相同，若从这个袋中任取2个珠子，都是蓝色珠子的概率是（ ）A、 B、 C、 D、9. 对于 y=2（x-3）2+2 的图象下列叙述正确的是 （ ）A、顶点坐标为(－3，2) B、对称轴为直线y＝3 C、当 x≥3时，y随x增大而增大 D、当≤3时，y随x增大而减小10. 将抛物线 y=x2-6x+5 向上平移2个单位长度，再向右平移1个单位长度后，得到的抛物线解析式是（ ）A、y=(x-4)2-6 B、y=(x-4)2-2 C、y=(x-2)2-2 D、y=(x-1)2-3二、填空题（本题有6小题，每小题5分，共30分）
-
11. 不透明的袋中装有2个红球和3个黑球，它们除颜色外没有任何其他区别，小红搅匀后从中随机摸出1个球，摸出红球的概率是 ．12. 从1至9这9个自然数中任取一个数，使它既是2的倍数又是3的倍数的概率是.
13. 若抛物线 y=x2+（k-1）x+（k+3） 经过原点，则k=.14. 抛掷一枚质地均匀的硬币2次，结果都是正面朝上的概率为 ．15. 从长度分别为2，4，6，7的四条线段中随机取三条，能构成三角形的概率是16. 如图，已知A1、A2、A3、A4、，…An 是x轴上的点，且OA1= A1A2=A2A3=A3A4=…=1，分别过点A1、A2、A3、A4、，…An 做x轴的垂线交二次函数 （x＞0）的图像于点P1、P2、P3、…、Pn . 若记△OA1P1的面积为S1 ， 过点P1做P1B1⊥A2P2于点B1 ， 记△P1B1P2的面积为S2 ， 过点P2做P2B2
P3B3于点B2 ， 记△P2B2P3的面积为S3 ， 依次进行下去，最后记△Pn－1B n－1P n的面积为Sn ， 则Sn= ． 
三、解答题（本题有8小题，第17题8分， 第18～20题每题8分，第21、22题10分23题12分，第24题14分，共80分．解答需写出必要的文字说明、演算步骤或证明过程）
-
17. 求下列二次函数图象的开口方向、顶点坐标和对称轴：(1)、y=-x2+2x-3(2)、y=x2-2x+18. 一个不透明的口袋里装有红、黄、绿三种颜色的球（除颜色不同外其余都相同），其中红球有2个，黄球有1个，从中任意摸出1个球是红球的概率为 ．(1)、袋中绿球的个数是个．(2)、从箱子中任意摸出一个球是黄球的概率是多少？(3)、第一次从袋中任意摸出1球，放回，搅匀，第二次再任意摸出1球，求两次都摸到红球的概率（用列表法或树状图表示）．19. 如图，有长为24米的篱笆，一面利用墙(图中的阴影部分就是墙，墙的最大可利用长度为9米)，围成中间隔有一道篱笆的长方形花圃. 花圃的宽AB为x米，面积为S平方米．
(1)、求S与x的函数关系式及自变量x的取值范围；(2)、当x为多少时，围成的花圃面积最大？最大面积是多少？20. 从3名男生和2名女生中随机抽取2022年杭州亚运会志愿者．求下列事件的概率：(1)、随机抽取1名，恰好是女生；(2)、（用列表法或树状图表示）随机抽取2名，恰好是1名男生和1名女生．21. 某商品的进价为每件40元，售价为每件50元，每个月可卖出210件；如果每件商品的售价每上涨1元，则每个月少卖10件（每件售价不能高于65元）．设每件商品的售价上涨x 元（ 为正整数），每个月的销售利润为 y元．
(1)、求y 与x 的函数关系式并直接写出自变量的取值范围；(2)、每件商品的售价定为多少元时，每个月可获得最大利润？最大的月利润是多少元？(3)、为了使顾客尽量满意，每件商品的售价定为多少元时，每个月的利润恰为2200元？22. 如图，甲、乙两人在玩转盘游戏时，准备了两个可以自由转动的转盘A，B，每个转盘被分成面积相等的几个扇形，并在每一个扇形内标上数字．游戏规则：同时转动两个转盘，当转盘停止后，指针所指区域的数字之和为0时，甲获胜；数字之和为1时，乙获胜．如果指针恰好指在分割线上，那么重转一次，直到指针指向某一区域为止．
(1)、用画树状图或列表法求乙获胜的概率；(2)、这个游戏规则对甲、乙双方公平吗？请判断并说明理由．23. 如图① ，已知抛物线 （a≠0）与x轴交于点A（1，0）和点B（－3，0），与y轴交于点C ．
(1)、求抛物线的表达式；(2)、设抛物线的对称轴与x轴交于点N ，问在对称轴上是否存在点P ， 使△CNP为等腰三角形？若存在，请直接写出所有符合条件的点P的坐标；若不存在，请说明理由．(3)、如图②，若点E为第三象限抛物线上一动点，连结BE、CE ， 求四边形BOCE面积的最大值，并求此时E点的坐标.24. 如图，抛物线y＝nx2－11nx＋24n（n＜0）与x轴交于B ， C两点（点B在点C的左侧），抛物线上另有一点A在第一象限内，且∠BAC＝90°．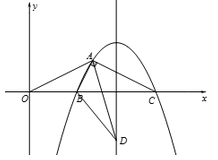
(1)、点B的坐标为 ， 点C的坐标为 ．(2)、连结OA ， 若OA＝AC ．① 求n的值；
② 若点D为抛物线对称轴上一点，连结AD ， BD ， 则当△AOB与△ADB面积相等时，求出所有满足条件的点D的坐标.