湖北省孝感市孝南区2021届九年级上学期数学10月月考试卷

试卷更新日期：2020-10-20 类型：月考试卷

进入出卷网下载

一、选择题

1. 若方程（m﹣2）x²﹣3x﹣2＝0是关于x的一元二次方程，则m的取值范围是（）

A、m＞2 B、m≠2 C、m＞0 D、m≠0

查看试题解析
2. 把一元二次方程（1﹣x）（2﹣x）=3﹣x²化成一般形式ax²+bx+c=0（a≠0）其中a、b、c分别为（　　）

A、2、3、﹣1 B、2、﹣3、﹣1 C、2、﹣3、1 D、2、3、1

查看试题解析
3. $y = {(x - 2)}^{2} + 2$ 抛物线的顶点坐标是（）

A、(－2，2) B、(2，－2) C、(2，2) D、(－2，－2)

查看试题解析
4. 一元二次方程 $x^{2} - 2 x - m = 0$ 用配方法解该方程，配方后的方程为（）

A、 ${(x - 1)}^{2} = m + 1$ B、 ${(x - 1)}^{2} = m - 1$ C、 ${(x - 1)}^{2} = 1 - m$ D、 ${(1 - x)}^{2} = m + 1$

查看试题解析
5. 如果a是一元二次方程 $x^{2} - 3 x + m = 0$ 的一个根，-a是一元二次方程 $x^{2} + 3 x - m = 0$ 的一个根，那么a的值是（）

A、1或2 B、0或－3 C、 $- 1$ 或 $- 2$ D、0或3

查看试题解析
6. 要得到抛物线 $y = 3 {(x + 2)}^{2} + 3$ ，可以将抛物线 $y = 3 x^{2}$ （）

A、向左平移2个单位长度，再向上平移3个单位长度 B、向左平移2个单位长度，再向下平移3个单位长度 C、向右平移2个单位长度，再向上平移3个单位长度 D、向右平移2个单位长度，再向下平移3个单位长度.

查看试题解析
7. 已知等腰三角形两边长分别是方程 $x^{2} - 6 x + 8 = 0$ 的两个根，则三角形周长为（）

A、6 B、8 C、10 D、8或10

查看试题解析
8. 为执行“均衡教育"政策，某县2017年投入教育经费 $2500$ 万元，预计到2019年底三年累计投入 $1.2$ 亿元.若每年投人教育经费的年平均增长百分率为x，则下列方程正确的是（）

A、 $2500 (1 + x^{2}) = 1.2$ B、 $2500 (1 + x^{2}) = 12000$ C、 $2500 + 2500 (1 + x) + 2500 (1 + x^{2}) = 1.2$ D、 $2500 + 2500 (1 + x) + 2500 {(1 + x)}^{2} = 12000$

查看试题解析
9. 二次函数 $y = - {(x + b)}^{2} - c$ 的图象如图所示，则一次函数y＝bx＋c的图象不经过（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
10. 如图是一个三角点阵，从上向下数有无数多行，其中第一行一个点，第二行两个点……第n行有n个点……，已知前m行的点数和为210，则m的值为（）

A、19 B、20 C、21 D、22

查看试题解析

二、填空题

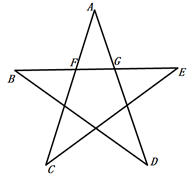
11. 方程x²＝2x的解是.

查看试题解析
12. 若 $| b - 1 | + \sqrt{a - 4} = 0$ ，且一元二次方程 ${kx}^{2} + ax + b = 0$ 有实数根，则k的取值范围是.

查看试题解析
13. 若m，n是方程x²＋3x﹣2＝0的根，则2m²＋8m＋2n﹣5的值是.

查看试题解析
14. 关于x的一元二次方程x²﹣（2m﹣1）x＋m²＋1＝0，设x₁ ， x₂分别是方程的两个根，且满足x₁²＋x₂²＝x₁x₂＋10，则m的值为.

查看试题解析
15. 小明设计了一个魔术盒，当任意实数对(a，b)进入其中时，会得到一个新的实数 $a^{2} + 3 b - 3$ ，例如把(2，－5)放入其中，就会得到 $2^{2} + 3 \times (- 5) - 3 = - 14$ ，现将实数对(m，－3m)放入其中，得到实数－23，则m＝.

查看试题解析
16. 五角星是常见的图案，如图，在正五角星中存在黄金分割数，有 $\frac{F G}{B F} = \frac{B F}{B G}$ ，已知BG＝2，则FG＝　

查看试题解析

三、解答题

17. 解方程

(1)、 ${(1 + x)}^{2} = 1.44$

(2)、 ${(2 x + 1)}^{2} = {(3 x - 1)}^{2}$

查看试题解析
18. 已知抛物线对称轴为直线x＝3，且抛物线经过点A(2，0)，B(1，6)，求抛物线解析式.

查看试题解析
19. 新年伊始，新冠肺炎肆虐全球，两名游客在非洲旅游时不慎感染新冠肺炎，经过两轮传染后，共有名1800人受到感染，每轮传染中平均一人传染多少个人？

查看试题解析
20. 已知函数 $y = (m + 3) x^{m^{2} + 3 m - 2}$ 是关于x的二次函数.

(1)、求m的值.

(2)、当m为何值时，该函数图象的开口向下？

(3)、当m为何值时，该函数有最小值，最小值是多少？

查看试题解析
21. 已知关于x的一元二次方程x²﹣6x﹣k²=0（k为常数）．

(1)、求证：方程有两个不相等的实数根；

(2)、设x₁ ， x₂为方程的两个实数根，且x₁+2x₂=14，试求出方程的两个实数根和k的值．

查看试题解析
22. 如图，Rt△ABC中∠B＝90°，AC＝10cm，BC＝6cm，现有两个动点P、Q分别从点A和点B同时出发，其中点P以2cm/s的速度，沿AB向终点B移动；点Q以1cm/s的速度沿BC向终点C移动，其中一点到终点，另一点也随之停止.连结PQ，设动点运动时间为x秒.

(1)、用含x的代数式表示BQ为cm，PB为cm；

(2)、是否存在x的值，使得四边形APQC的面积等于20cm²？若存在，请求出此时 $x$ 的值；若不存在，请说明理由.

查看试题解析
23. 百货大楼服装柜在销售中发现：某品牌童装每件成本60元，现以每件100元销售，平均每天可售出20件．为了迎接“五•一”劳动节，商场决定采取适当的降价措施，以扩大销售量，增加盈利，尽量减少库存．经市场调查发现：如果每件童装降价1元，那么平均每天就可多销售2件．要想平均每天销售这种童装盈利1200元，请你帮商场算一算，每件童装应定价多少元？

查看试题解析
24. 如图，已知抛物线 $y = a {(x - h)}^{2} + k$ 与x轴有一个交点为A(3，0)，与y轴的交点为B(0，3)，对称轴是直线x＝1.

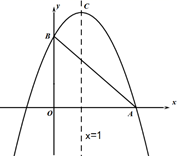(1)、求抛物线的函数解析式；

(2)、在抛物线上是否存在一动点M，使得 $S_{Δ A O B} = S_{Δ A M B}$ ，若存在，求出M点坐标；若不存在，说明理由.

查看试题解析