广东省深圳市南山区2019-2020学年七年级上学期数学期末试卷
试卷更新日期:2020-10-20 类型:期末考试
一、单选题
-
1. 下面几何体中为圆柱的是( )A、
 B、
B、 C、
C、 D、
D、 2. 根据国家气象局统计,全球平均每年发生雷电次数约为16000000次,将16000000用科学记数法表示为( )A、1.6×108 B、1.6×107 C、16×106 D、1.6×1063. 如图所示,能用 , , 三种方法表示同一个角的图形是( )A、
2. 根据国家气象局统计,全球平均每年发生雷电次数约为16000000次,将16000000用科学记数法表示为( )A、1.6×108 B、1.6×107 C、16×106 D、1.6×1063. 如图所示,能用 , , 三种方法表示同一个角的图形是( )A、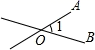 B、
B、 C、
C、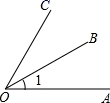 D、
D、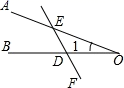 4. 将 写成省略括号的和的形式是( )A、 B、 C、 D、5. 一件商品的进价是a元,提价30%后出售,则这件商品的售价是( )A、0.7a元 B、1.3a元 C、a元 D、3a元6. 下列判断错误的是( )A、多项式 是二次三项式 B、单项式 的系数是 ,次数是9 C、式子 , , , , 都是代数式 D、当 时,关于x,y的代数式 中不含二次项7. 下列各组单项式中,是同类项的是( )A、a2与2a B、5ab与5abc C、 m2n与﹣ nm2 D、x3与238. 北京海淀区某中学经过食堂装修后重新营业,同学们很高兴品尝各种美食菜品某同学想要得到本校食堂最受同学欢迎的菜品,以下是排乱的统计步骤:
4. 将 写成省略括号的和的形式是( )A、 B、 C、 D、5. 一件商品的进价是a元,提价30%后出售,则这件商品的售价是( )A、0.7a元 B、1.3a元 C、a元 D、3a元6. 下列判断错误的是( )A、多项式 是二次三项式 B、单项式 的系数是 ,次数是9 C、式子 , , , , 都是代数式 D、当 时,关于x,y的代数式 中不含二次项7. 下列各组单项式中,是同类项的是( )A、a2与2a B、5ab与5abc C、 m2n与﹣ nm2 D、x3与238. 北京海淀区某中学经过食堂装修后重新营业,同学们很高兴品尝各种美食菜品某同学想要得到本校食堂最受同学欢迎的菜品,以下是排乱的统计步骤:①从扇形图中分析出最受学生欢迎的菜品;
②去食堂收集同学吃饭选择的菜品名称和人数;
③绘制扇形图来表示各个种类产品所占的百分比;
④整理所收集的数据,并绘制频数分布表;
正确统计步骤的顺序是( )
A、②→③→①→④ B、②→④→③→① C、①→②→④→③ D、③→④→①→②9. 已知关于x的一元一次方程 的解为x=-3,那么关于y的一元一次方程 的解为( )A、y=1 B、y=-1 C、y=-3 D、y=-410. 小明在某月的日历上圈出了三个数a,b,c,并求出了它们的和为39,则这三个数在日历中的排位位置不可能的是( )A、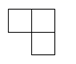 B、
B、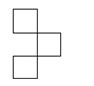 C、
C、 D、
D、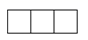 11. 已知三条不同的射线OA、OB、OC有下列条件:①∠AOC=∠BOC ②∠AOB=2∠AOC ③∠AOC+∠COB=∠AOB ④∠BOC= ∠AOB,其中能确定OC平分∠AOB的有( )A、4个 B、3个 C、2个 D、1个12. 下列说法:①经过一点有无数条直线;②两点之间线段最短;③经过两点,有且只有一条直线;④若线段AM等于线段BM,则点M是线段AB的中点;⑤连接两点的线段叫做这两点之间的距离.其中正确的个数为( )A、1个 B、2个 C、3个 D、4个
11. 已知三条不同的射线OA、OB、OC有下列条件:①∠AOC=∠BOC ②∠AOB=2∠AOC ③∠AOC+∠COB=∠AOB ④∠BOC= ∠AOB,其中能确定OC平分∠AOB的有( )A、4个 B、3个 C、2个 D、1个12. 下列说法:①经过一点有无数条直线;②两点之间线段最短;③经过两点,有且只有一条直线;④若线段AM等于线段BM,则点M是线段AB的中点;⑤连接两点的线段叫做这两点之间的距离.其中正确的个数为( )A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 用一个平面截下列几何体:①长方体,②六棱柱,③球,④圆柱,⑤圆锥,截面能得到三角形的是 (填写序号即可)14. 通常在生产图纸上,对每个产品的合格范围有明确的规定.例如,图纸上注明一个零件的直径是 , 表示这个零件直径的标准尺寸是30mm,实际产品的直径最大可以是30.03mm,最小可以是15. 已知 ,则 的值是16. 定义一种树对正整数n的“F”运算:①当n的奇数时F(n)=3n+1;②当n为偶数时,F(n)= (其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=24则:

若n=13,则第2019次“F”运算的结果是
三、解答题
-
17. 计算:(1)、(2)、(3)、先化简,再求值: ,其中 ,b=218. 解下列方程(1)、(2)、19. 如图所示,已知线段AB,点P是线段AB外一点.
 (1)、按要求画图,保留作图痕迹;
(1)、按要求画图,保留作图痕迹;①作射线PA,作直线PB;
②延长线段AB至点C,使得AC=2AB,再反向延长AC至点D,使得AD=AC.
(2)、若(1)中的线段AB=2cm,求出线段BD的长度.20. 某校九年级(1)班部分学生接受一次内容为“最适合自己的考前减压方式”的调查活动,收集整理数据后,老师将减压方式分为五类,并绘制了如图①②两幅不完整的统计图,请根据图中的信息解答下列问题. (1)、九年级(1)班接受调查的学生共有多少名?(2)、补全条形统计图,并计算扇形统计图中的“体育活动C”所对应的圆心角度数.21. 如图,∠AOB是平角,∠COD=90°,OE平分∠AOC,OF平分∠BOC.
(1)、九年级(1)班接受调查的学生共有多少名?(2)、补全条形统计图,并计算扇形统计图中的“体育活动C”所对应的圆心角度数.21. 如图,∠AOB是平角,∠COD=90°,OE平分∠AOC,OF平分∠BOC. (1)、求∠EOF的度数.(2)、若∠COE=70°,求∠DOF的度数.22. 用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成。硬纸板以如图两种方式裁剪(裁剪后边角料不再利用)
(1)、求∠EOF的度数.(2)、若∠COE=70°,求∠DOF的度数.22. 用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成。硬纸板以如图两种方式裁剪(裁剪后边角料不再利用)A方法:剪6个侧面; B方法:剪4个侧面和5个底面。

现有19张硬纸板,裁剪时x张用A方法,其余用B方法。
(1)、用x的代数式分别表示裁剪出的侧面和底面的个数;(2)、若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?23. 已知a是最大的负整数,b是-5的相反数,c= ,且a、b、c分别是点A、B、C在数轴上对应的数.若动点P从点A出发沿数轴正方向运动,动点Q同时从点B出发也沿数轴正方向运动,点P的速度是每秒3个单位长度,点Q的速度是每秒1个单位长度.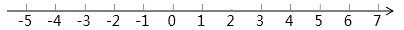 (1)、求a、b、c的值;(2)、P、Q同时出发,求运动几秒后,点P可以追上点Q?(3)、在(2)的条件下,P、Q出发的同时,动点M从点C出发沿数轴正方向运动,速度为每秒6个单位长度,点M追上点Q后立即返回沿数轴负方向运动,追上后点M再运动几秒,M到Q的距离等于M到P距离的两倍?
(1)、求a、b、c的值;(2)、P、Q同时出发,求运动几秒后,点P可以追上点Q?(3)、在(2)的条件下,P、Q出发的同时,动点M从点C出发沿数轴正方向运动,速度为每秒6个单位长度,点M追上点Q后立即返回沿数轴负方向运动,追上后点M再运动几秒,M到Q的距离等于M到P距离的两倍?